相关试卷
- 3.2整式的加减提升课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学六年级上学期期中仿真模拟试卷一
- 3.2 整式的加减基础课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷二(范围:1.1-4.2)
- 2.1《 事件的可能性》(2)—浙教版数学九年级上册课堂分层训练
- 浙教版数学八年级上册4.3.2 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版 数学八年级上册4.3.1 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版数学八年级上册4.2 用方向和距离确定物体的位置 同步分层练习
- 浙江省九年级上学期数学期中仿真模拟试题(一)
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
-
1、四边形是正方形,E、F分别是和的延长线上的点,且 , 连接 .
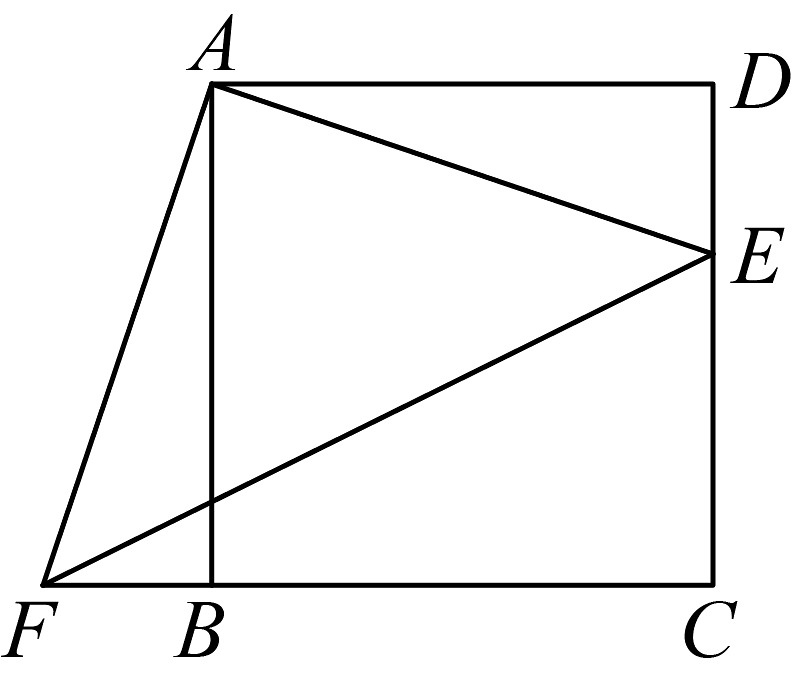 (1)、试判断的形状,并说明理由;(2)、填空:可以由绕旋转中心 点,按顺时针方向旋转 度得到;(3)、若 , 则四边形的面积为 . (直接写结果)
(1)、试判断的形状,并说明理由;(2)、填空:可以由绕旋转中心 点,按顺时针方向旋转 度得到;(3)、若 , 则四边形的面积为 . (直接写结果) -
2、如图,在平面直角坐标系中,将边长为的正方形绕点顺时针旋转后得到正方形 . 依此方式连续旋转次得到正方形 , 那么点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图,RtABC中,∠A=90°,∠ABC=40°,将RtABC绕着点C逆时针旋转得RtEDC,且点E正好落在BC上,连接BD,则∠CBD的度数为( )
 A、40° B、55° C、60° D、65°
A、40° B、55° C、60° D、65° -
4、如图,与关于点成中心对称,下列说法:
①;②;③;④与的面积相等,其中正确的有( )
 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个 -
5、如图 , 已知是的外接圆, , 点为的中点,过作于 , 交于点 , 交于点 .
 (1)、求证:;(2)、如图 , 延长 , 交于点 , 连接 .
(1)、求证:;(2)、如图 , 延长 , 交于点 , 连接 .求证:;
若 , 求的值.(用含的式子表示)
-
6、已知关于x的二次函数(m是常数).(1)、若该二次函数的图象经过点 ,
①求m的值;②若该二次函数的图象与x轴交于点B,C(点B在点C的左侧),求的面积;
(2)、若该二次函数的图象与y轴交于点P,求点P纵坐标的最大值; -
7、计算: .
-
8、如图,在矩形中, , , , 分别为 , 边的中点.动点从点出发沿向点运动,同时,动点从点出发沿向点运动,连接 , 过点作于点 , 连接 . 若点的速度是点的速度的2倍,在点从点运动至点的过程中,线段长度的最大值为 , 线段长度的最小值为 .

-
9、如图,点是正十二边形的中心,于点 , 则正确的是( )
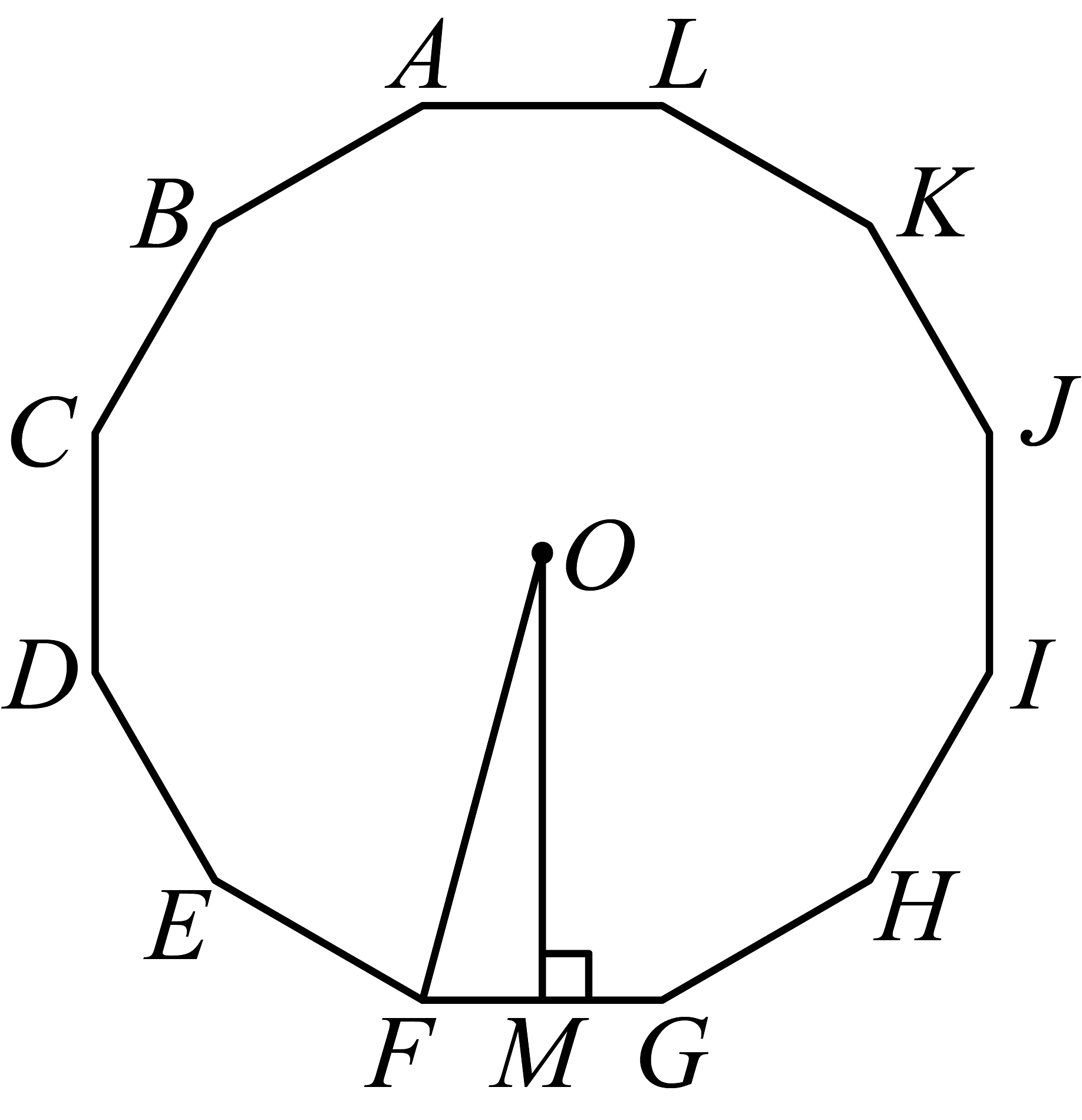 A、 B、 C、 D、
A、 B、 C、 D、 -
10、已知点C把线段黄金分割,且 , 那么下列等式中,成立的是( )A、 B、 C、 D、
-
11、已知二次函数 .(1)、求该函数图象的顶点坐标、对称轴以及与x轴的交点坐标;(2)、当时,求y的最大值与最小值之差;(3)、当时,求y的最小值.(可用含k的代数式表示)
-
12、如图,是半圆O的直径,C,D是圆上的两点,且 , 与交于点E.
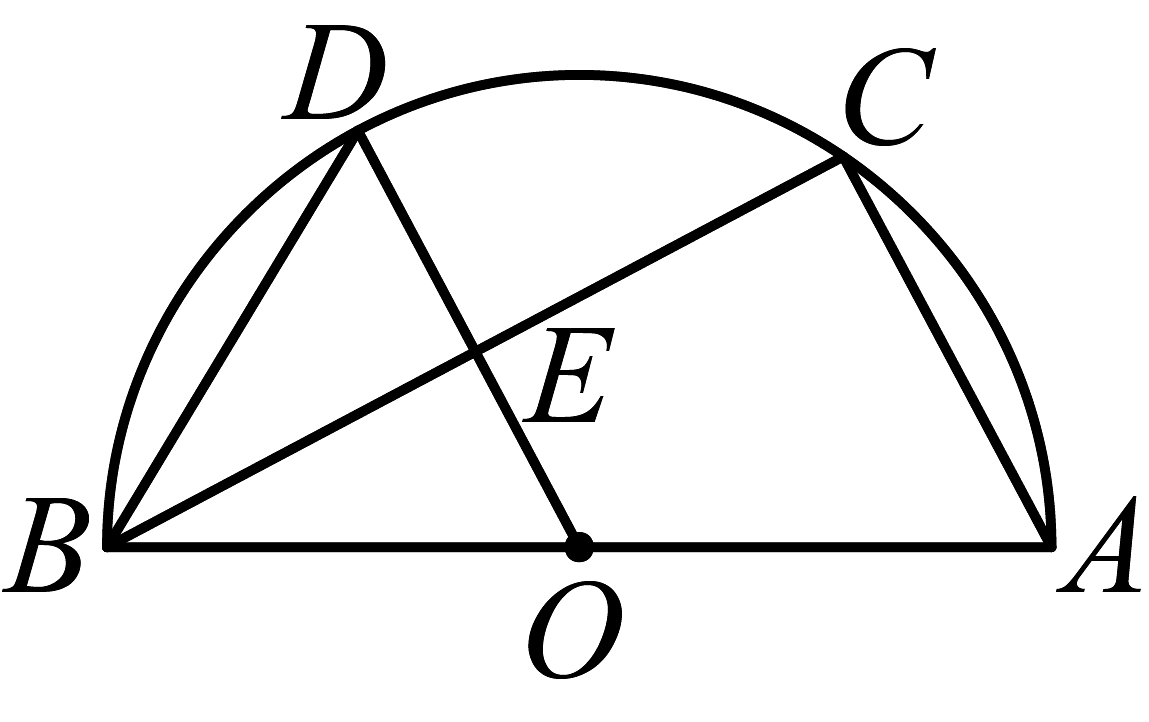 (1)、求证:E为的中点.(2)、若 , , 求的长度.
(1)、求证:E为的中点.(2)、若 , , 求的长度. -
13、如图,的弦 , 相交于点E,且 , 求证: .
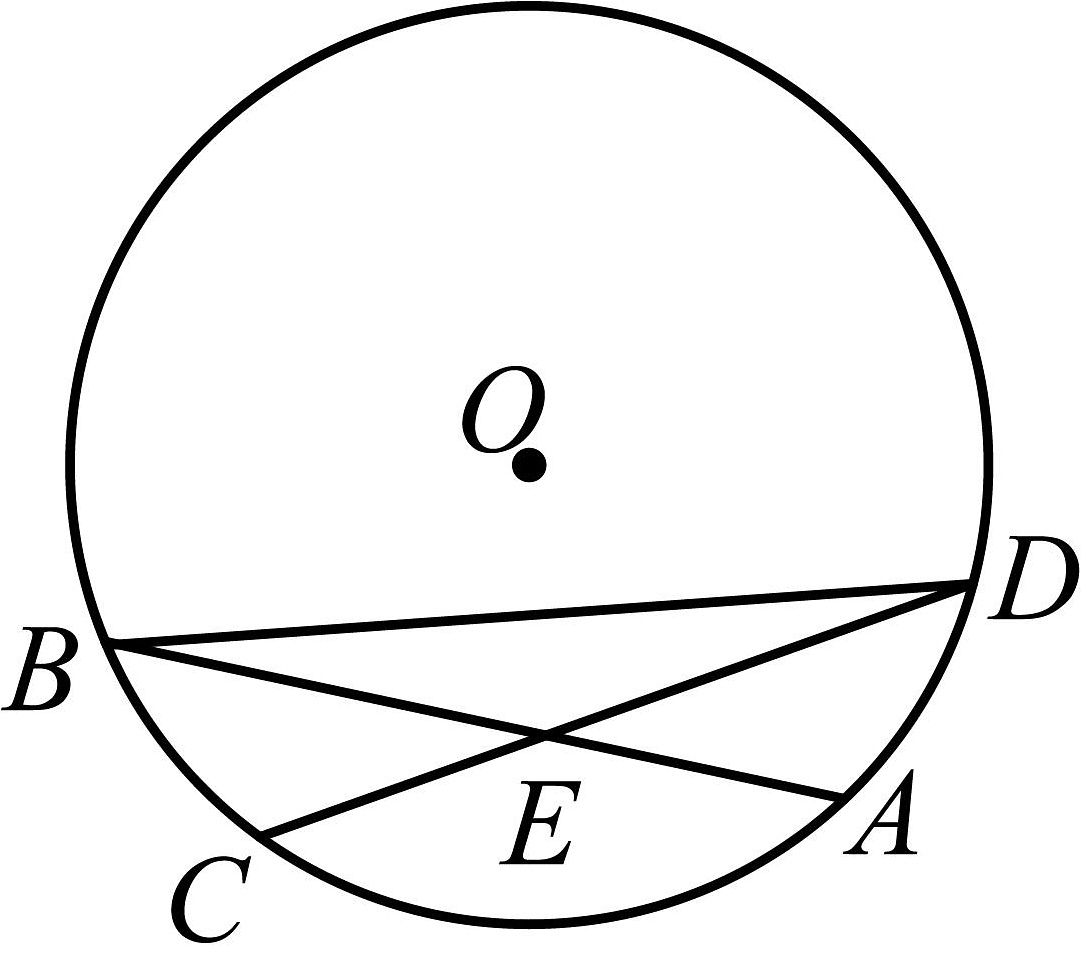
-
14、如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有(填序号).

-
15、如果二次函数(为常数)的图象上有两点和 , 那么(填“”、“”或“”).
-
16、某林业局将一种树苗移植成活的情况绘制成如统计图,由此可估计这种树苗移植成活的概率约为( )
 A、0.95 B、0.90 C、0.85 D、0.80
A、0.95 B、0.90 C、0.85 D、0.80 -
17、如图1,是的直径,点D为下方上一点,点C为弧的中点,连结 , , .
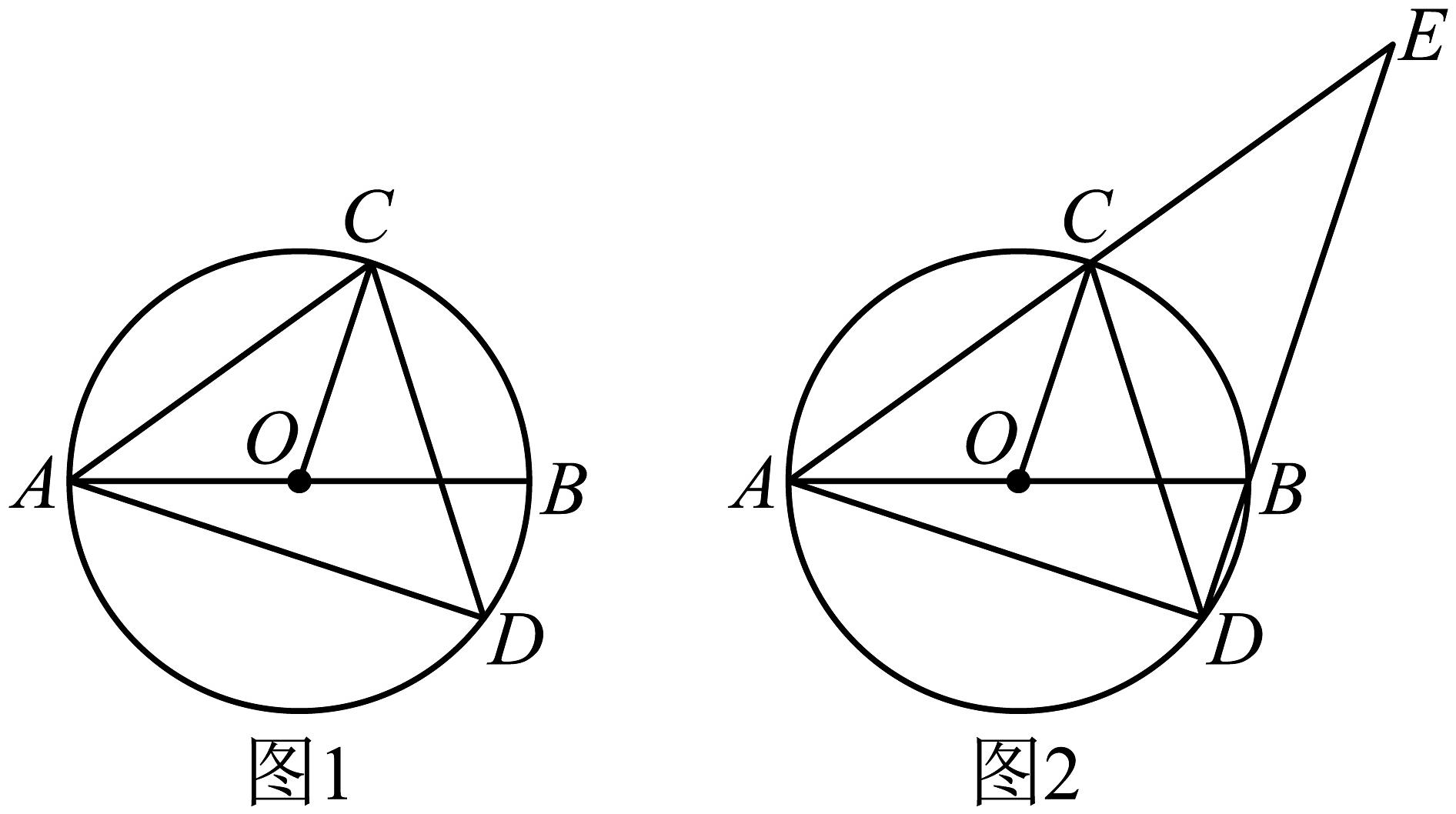 (1)、求证:平分 .(2)、如图2,延长 , 相交于点E.
(1)、求证:平分 .(2)、如图2,延长 , 相交于点E.①求证: .
②若 , , 求的半径.
-
18、如何拟定运动员拍照记录的方案?
素材1
图1是单板滑雪运动员从大跳台滑雪场地滑出的场景,图2是跳台滑雪场地的横截面示意图.垂直于水平底面 , 点D到A之间的滑道呈抛物线型.已知 , , 且点B处于跳台滑道的最低处.
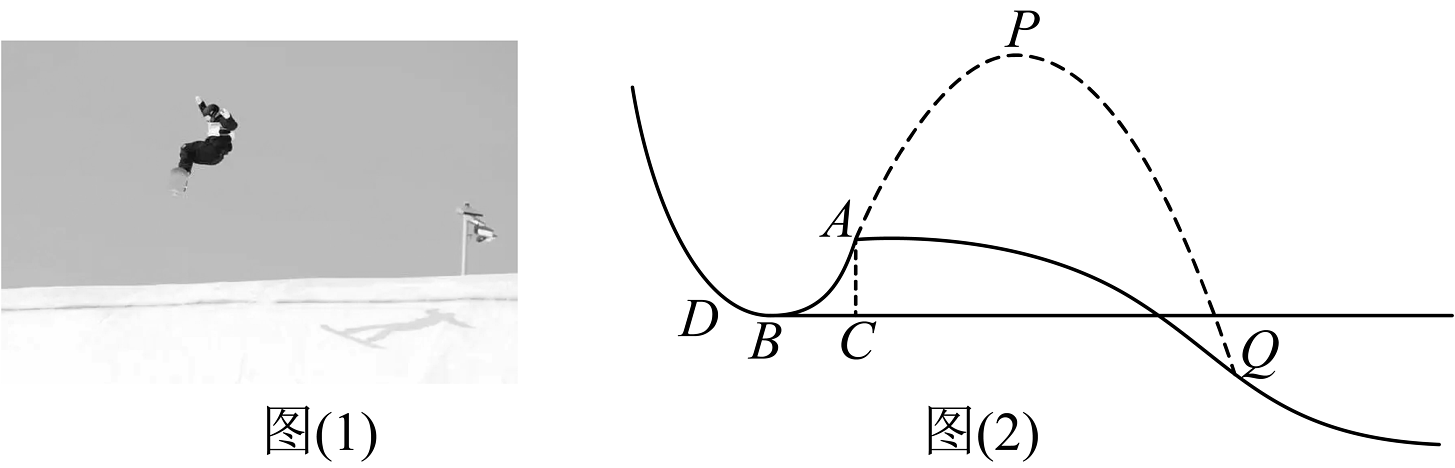
素材2
如图3,某运动员从点A滑出后的路径满足以下条件:
①运动员滑出路径与D、A之间的抛物线形状相同.
②该运动员在底面上方竖直距离处达到最高点P.
③落点Q在底面下方竖直距离 .

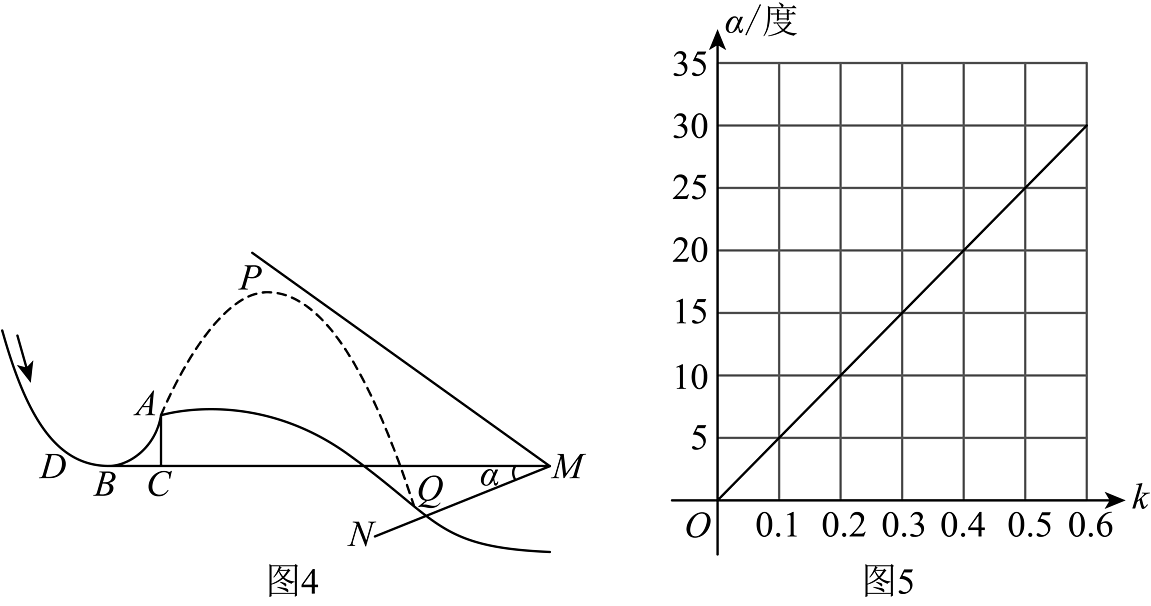
素材3
高速摄像机能高度还原运动员的精彩瞬间,如图4,有一台摄像机M进行跟踪拍摄:
①它与点B位于同一高度,且与点B距离;
②运动过程需在摄像头视角范围内才能记录,记摄像头的俯角为α;
③在平面直角坐标系中,设射线的解析式为 , 其比
例系数k和俯角α的函数关系如图5所示.
问题解决
任务1
确定D、A之间滑道的形状
在图2中建立适当的平面直角坐标系,求滑道所在抛物线的函数表达式.
任务2
确定运动员达到最高点的位置
在同一平面直角坐标系中,求运动员到达最高处时与点A的水平距离.
任务3
确定拍摄俯角α
若要求运动员的落点Q必须在摄像机M的视角范围内,则俯角α至少多少度(精确到个位)?
-
19、如图,在中, , 以为直径的分别交 , 于点 , , 连接交于点 .
 (1)、求证:;(2)、连接 , 若 , , 求的长.
(1)、求证:;(2)、连接 , 若 , , 求的长. -
20、在平面直角坐标系中,抛物线的顶点为 , 且过点 .(1)、求抛物线的函数表达式;(2)、求将抛物线向左平移几个单位,可使得平移后所得抛物线经过原点?