相关试卷
- 3.2整式的加减提升课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学六年级上学期期中仿真模拟试卷一
- 3.2 整式的加减基础课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷二(范围:1.1-4.2)
- 2.1《 事件的可能性》(2)—浙教版数学九年级上册课堂分层训练
- 浙教版数学八年级上册4.3.2 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版 数学八年级上册4.3.1 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版数学八年级上册4.2 用方向和距离确定物体的位置 同步分层练习
- 浙江省九年级上学期数学期中仿真模拟试题(一)
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
-
1、将抛物线先向右平移2个单位长度,再向下平移1个单位长度,平移后对应的二次函数解析式为( )A、 B、 C、 D、
-
2、下列各组图中,是相似图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
3、下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、
-
4、如图,已知直线y=x﹣4分别与x轴,y轴交于A,B两点,直线OG:y=kx(k<0)交AB于点D.
(1)求A,B两点的坐标;
(2)如图1,点E是线段OB的中点,连接AE,点F是射线OG上一点,当OG⊥AE,且OF=AE时,求EF的长;
(3)如图2,若k= , 过B点BCOG,交x轴于点C,此时在x轴上是否存在点M,使∠ABM+∠CBO=45°,若存在,求出点M的坐标;若不存在,请说明理由.

-
5、勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
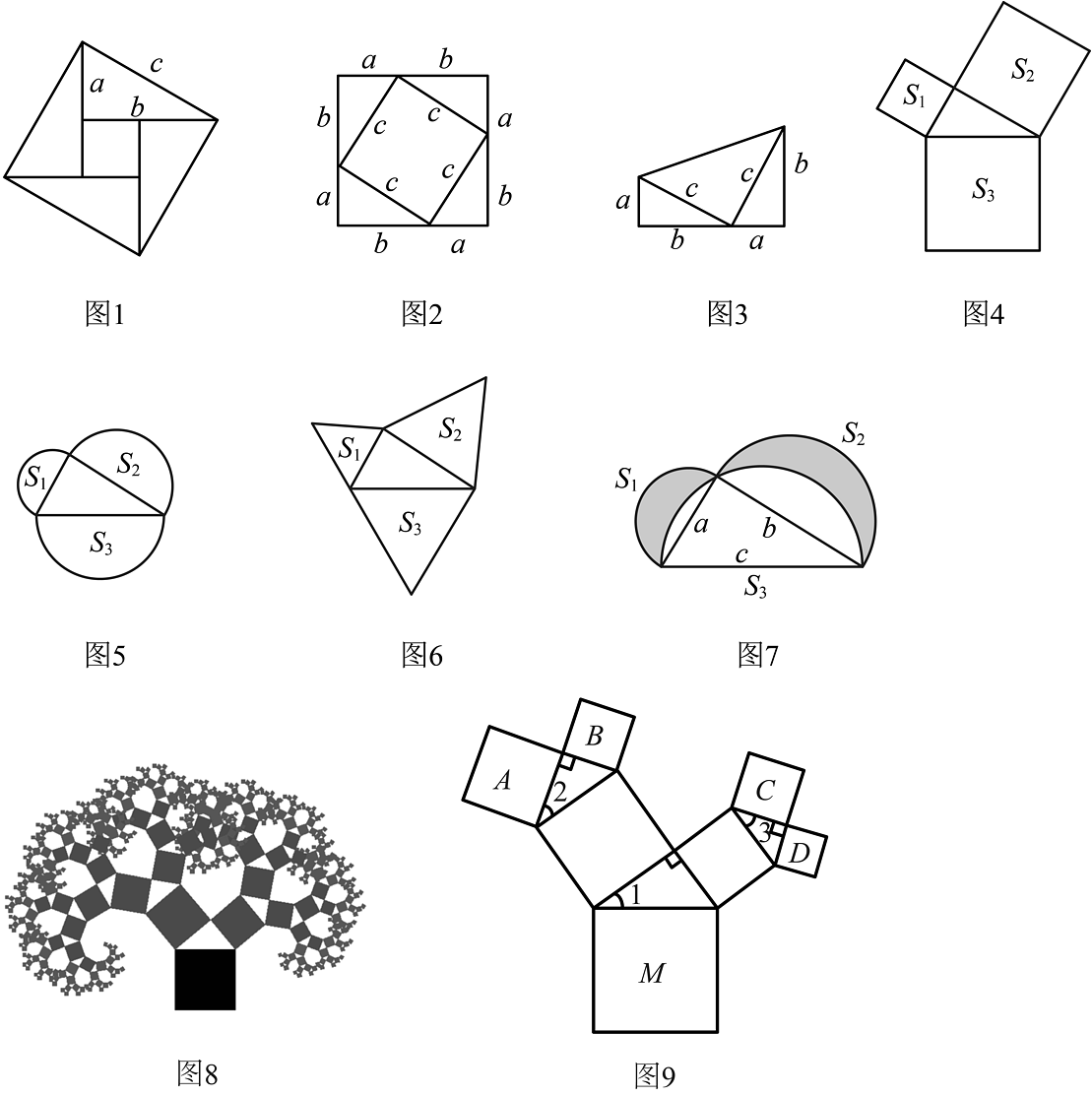 (1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);
(1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)、①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足的有______个;②如图7所示,分别以直角三角形两直角边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , , 直角三角形面积为 , 请判断 , , 的关系并证明;
(3)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知 , 则当变化时,回答下列问题:(结果可用含m的式子表示)则:①______.
②b与c的关系为______,a与d的关系为______.
-
6、周末,小丽和爸爸、妈妈一家三口去杨梅园游玩.已知该杨梅园内的杨梅单价是每千克40元.为满足客户需求,该杨梅园现推出两种不同的销售方案:
甲方案:游客进园需购买30元的门票,采摘的杨梅按原价的六折收费;
乙方案:游客进园不需购买门票,采摘的杨梅在10千克以内按原价收费、超过10千克后,10千克部分按原价收费,超过部分按原价的五折收费.
设采摘量为x千克,按甲方案所需总费用为元,按乙方案所需总费用为元.
(1)、当采摘量超过10千克时,分别求出、关于x的函数表达式;(2)、若采摘量为30千克,选择哪种方案更划算?请说明理由. -
7、在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
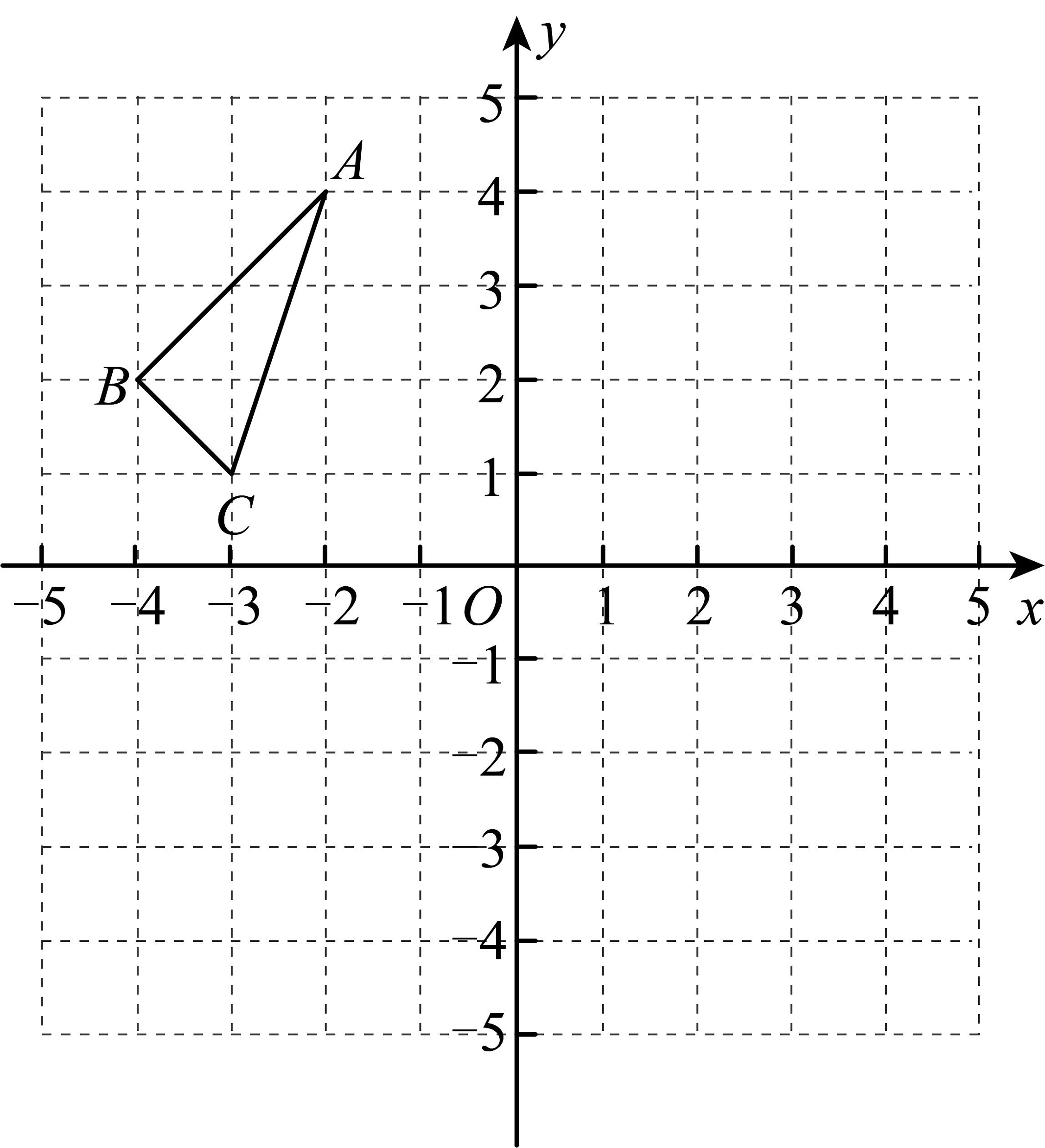 (1)、和关于x轴对称,请在坐标系中画出;(2)、求的面积;(3)、在x轴上画出点P,使得有最小值,并保留找该点的痕迹,求出的最小值.
(1)、和关于x轴对称,请在坐标系中画出;(2)、求的面积;(3)、在x轴上画出点P,使得有最小值,并保留找该点的痕迹,求出的最小值. -
8、规律探索图:如图,认真分析各式,然后解答问题.
, (是的面积);
, (是的面积);
, (是的面积);
……
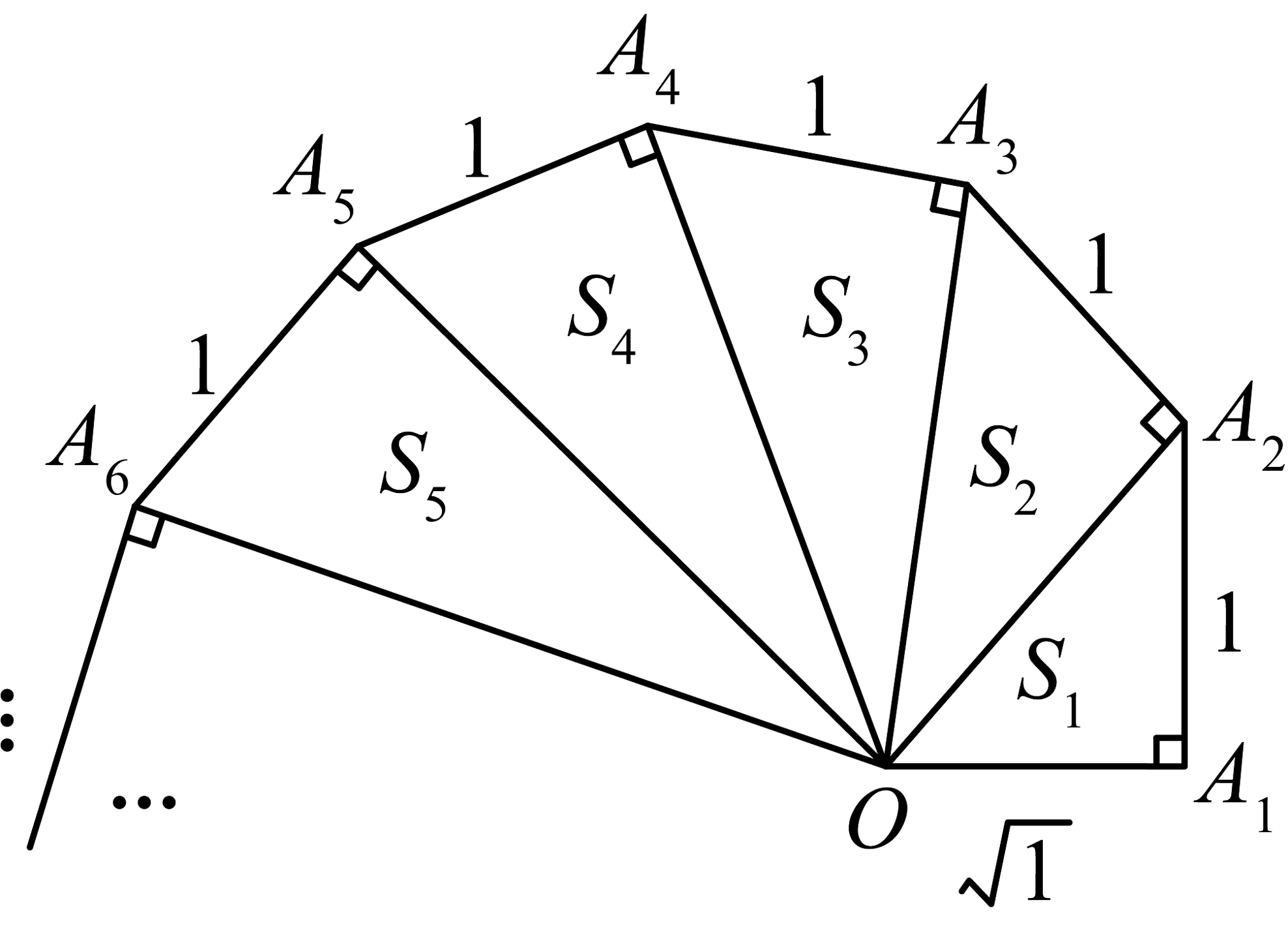 (1)、;(2)、;(3)、求出的值.
(1)、;(2)、;(3)、求出的值. -
9、已知一次函数 .(1)、将下列表格补充完整 ,并在平面直角坐标系中画出这个函数的图象.
x
…
0
1
…
…
0
…
 (2)、当函数值y为10时,自变量x的值为______.
(2)、当函数值y为10时,自变量x的值为______. -
10、已知点 , 解答下列问题:(1)、点P在y轴上,求点P的坐标;(2)、点Q的坐标为 , 直线轴,求点P的坐标;
-
11、在中 , , 高 , 则 .
-
12、在平面直角坐标系中,A,B两点的坐标分别为 , , 则A,B两点间的距离为.
-
13、下列各式中是最简二次根式的有个.
-
14、三角形的三条边长为5,12,13,则它最长边上的高的长为( )A、12 B、5 C、 D、
-
15、在 , 3.14,…(相邻两个1之间0的个数依次加1),…(相邻两个4之间只有1个0),这五个数中,无理数有( )A、2个 B、3个 C、4个 D、5个
-
16、下列为勾股数的是( )A、 , , B、 C、 , , D、7,24,25
-
17、实数16的平方根是( )A、4 B、 C、 D、
-
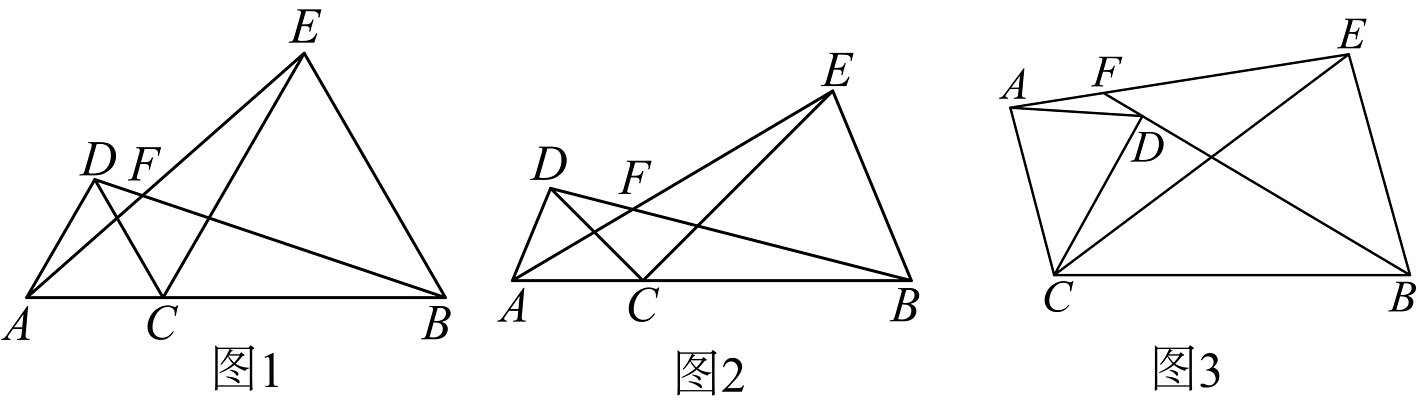
18、已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE, , 直线AE与BD交于点F.
(1)如图1,证明:△ACE≌△DCB;
(2)①如图1,若 , 则=________;
②如图2,若 , 则______;(用含的式子表示)
(3)将图2中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图3,试探究与的数量关系,并予以证明.
-
19、根据以下素材,探索完成任务.
素材1
随着数字技术、新能源、新材料等不断突破,我国制造业发展迎来重大机遇. 某工厂一车间借助智能化,对某款车型的零部件进行一体化加工,生产效率提升,该零件4月份生产100个,6月份生产144个.
素材2
该厂生产的零件成本为30元/个,销售一段时间后发现,当零件售价为40元/个时,月销售量为600个,在此基础上售价每上涨1元,则月销售量将减少10个.
问题解决
任务1
该车间4月份到6月份生产数量的平均增长率;
任务2
当零件的实际售价定为多少元时,每个月获得的销售利润最大?最大利润为多少?
-
20、已知关于x的一元二次方程 .(1)、若方程有实数根,求实数m的取值范围.(2)、若等腰三角形的其中一边为3,另两边是这个方程的两根,求m的值.