相关试卷
- 湘教版数学七年级上册3.4一元一次方程的应用 第二课时 同步分层练习
- 湘教版数学七年级上册3.4 一元一次方程的应用 第一课时 同步分层练习
- 浙教版数学八年级上册4.1.2 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册4.1.1 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测提升卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测培优卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测基础卷
- 北师大版数学八年级上册单元分层检测卷第二章 《实数》B卷
- 浙教版数学八年级上册3.5 一元一次不等式组 同步分层练习
- 湘教版数学七年级上册 3.3 一元一次方程的解法 第二课时 同步分层练习
-
1、已知 , 点 , 分别在射线 , 上,将线段绕点顺时针旋转 得到线段 , 过点作的垂线交射线于点.
 (1)、 如图①,当点在射线上时,求证:是的中点;(2)、 如图②,当点在内部时,作 , 交射线于点 , 用等式表示线段与的数量关系,并证明.
(1)、 如图①,当点在射线上时,求证:是的中点;(2)、 如图②,当点在内部时,作 , 交射线于点 , 用等式表示线段与的数量关系,并证明. -
2、已知是等腰直角三角形, ,点是所在平面内任意一点,绕点逆时针旋转 得到 , 连接 , , .
 (1)、 如图①,若点为内一点,求证:;(2)、 如图②,若点为边上一点, , , 求的长.
(1)、 如图①,若点为内一点,求证:;(2)、 如图②,若点为边上一点, , , 求的长. -
3、在平面直角坐标系中,的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
 (1)、 若和关于原点成中心对称,画出;(2)、 将绕点顺时针旋转 ,画出旋转后得到的 , 并写出点的坐标;(3)、 若在轴上存在一点 , 满足点到点与点的距离之和最小,请写出的最小值为.
(1)、 若和关于原点成中心对称,画出;(2)、 将绕点顺时针旋转 ,画出旋转后得到的 , 并写出点的坐标;(3)、 若在轴上存在一点 , 满足点到点与点的距离之和最小,请写出的最小值为. -
4、如图,在直角三角形中, , ,将三角形沿方向平移得到三角形.
 (1)、 求的度数;(2)、 若 , , 求的长.
(1)、 求的度数;(2)、 若 , , 求的长. -
5、如图,已知的顶点 , , .若向右平移4个单位长度,再向下平移3个单位长度得到 , 且点 , , 的对应点分别是 , , .
 (1)、 画出 , 并直接写出点的坐标;(2)、 若内有一点经过以上平移后的对应点为 , 直接写出点的坐标.
(1)、 画出 , 并直接写出点的坐标;(2)、 若内有一点经过以上平移后的对应点为 , 直接写出点的坐标. -
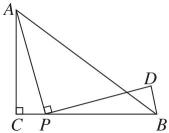
6、如图,在中, , , , 点是线段上的动点,连接 , 将线段绕点顺时针旋转 得到线段 , 连接 , 则的最小值是 .
-
7、如图,在平面直角坐标系中,点的坐标为 , 点在第一象限内,将沿轴正方向平移得到 , 若点的对应点在直线上,则点与其对应点之间的距离为.

-
8、如图,正方形内的图形来自中国古代的太极图,圆中的黑色部分和白色部分关于正方形的中心成中心对称,设黑色部分的面积为 , 正方形的边长为2,则 .

-
9、如图①,教室里有一个倒地的装垃圾的灰斗,与地面的夹角为 , ,小贤同学将它扶起平放在地面上(如图②),则灰斗柄绕点转动的角度为.

-
10、如图,长方形的顶点 , 分别在轴、轴上, , , 将长方形绕点顺时针旋转,每次都旋转 ,则第2 025次旋转结束时,点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,已知四边形是由四边形平移得到的,若 , , 则的长可能是( )
 A、3 B、5 C、8 D、11
A、3 B、5 C、8 D、11 -
12、如图,将线段先向左平移,使点与原点重合,再将所得到的线段绕原点旋转 得到线段 , 则点的对应点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,将绕点逆时针旋转,旋转角为 , 得到 , 点旋转后的对应点恰好在直线上,则下列结论不正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图,将绕点顺时针旋转 得到 , 则点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、如图所示,在中, ,将绕点逆时针旋转得到 , 点 , 的对应点分别为 , , 连接.当点 , , 在同一直线上时,旋转角的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、如果点在第二象限,那么点关于原点的对称点所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
17、下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、为了迎接“十一”长假的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋类型
甲
乙
进价/(元/双)
售价/(元/双)
240
160
已知用3 000元购进甲种运动鞋的数量与用2 400元购进乙种运动鞋的数量相同.
(1)、 求的值.(2)、 要使购进的甲、乙两种运动鞋共200双的总利润不少于21 700元,且不超过22 300元,该专卖店有几种进货方案?(利润 售价-进价)(3)、 在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,每双优惠元出售,乙种运动鞋价格不变,那么该专卖店要获得最大利润应如何进货? -
19、阅读下列材料:
, , , , ,
.
解答下列问题:
(1)、 在和式+…中,第6项为 , 第项是 .(2)、 上述求和的想法是:将和式中的各分数转化为两数之差,使得除首末两项外的中间各项可以抵消,从而达到求和的目的,受此启发,请你解下面的方程:. -
20、阅读下面的材料,然后解答问题.
解方程:.
解:设 , 则原方程化为 ,
方程两边同时乘 , 得 , 解得 或.
经检验,或 都是方程 的解.
当 时, , 解得;
当 时, , 解得.
经检验,或 都是原分式方程的解.
原分式方程的解为 或.
上述这种解分式方程的方法被称为换元法.
问题:模仿上述换元法解方程:.