相关试卷
- 浙教版数学七年级上册第1章有理数 40分钟单元效果评估卷
- 华东师大版数学八年级上学期期中仿真模拟试卷一(范围:10.1-12.2)
- 第四章《相交线和平行线》提升卷—华东师大版数学七(上)单元测
- 第三章《图形的初步认识》提升卷—华东师大版数学七(上)单元测
- 华东师大版数学七年级上学期期中仿真模拟试卷二(范围:1-2章)
- 沪科版数学九年级上册二次函数重难点题型梳理
- 浙教版数学八年级上学期重难点复习5:一元一次不等式(组)含参问题
- 浙教版数学八年级上学期重难点复习4:等腰三角形的分类讨论
- 浙教版数学八年级上学期重难点复习3:轴对称的应用
- 北师大版数学八年级上册单元分层检测卷第三章 《位置与坐标》B卷
-
1、如图1,在中, , , 为边上任一点,连接 , 延长到 , 使 . 设 .
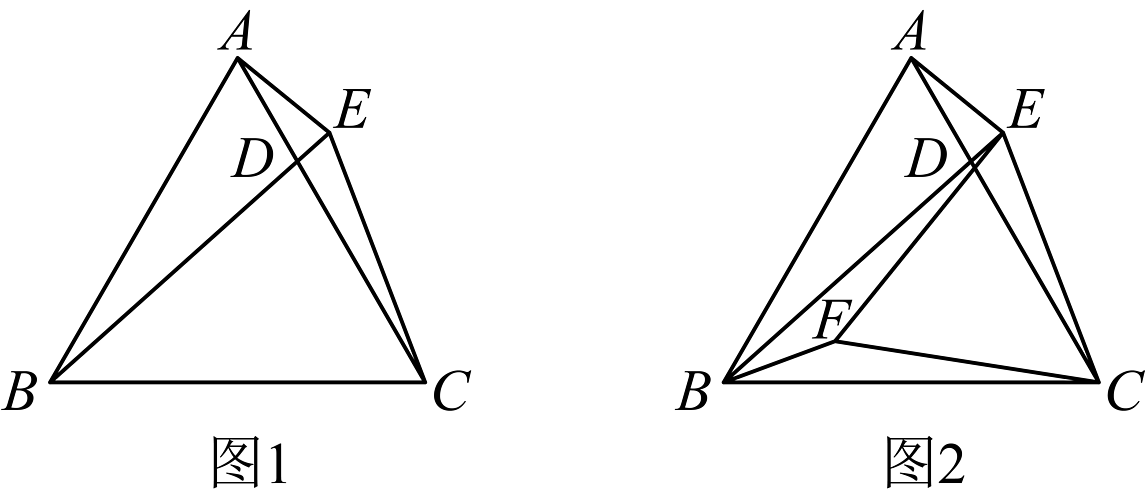 (1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明.
(1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明. -
2、如图,在 中, , 点 D是的延长线上一点,是线段的垂直平分线,交于点 F. 求证:点 E在线段的垂直平分线上.
-
3、如图,在边长为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
 (1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小.
(1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小. -
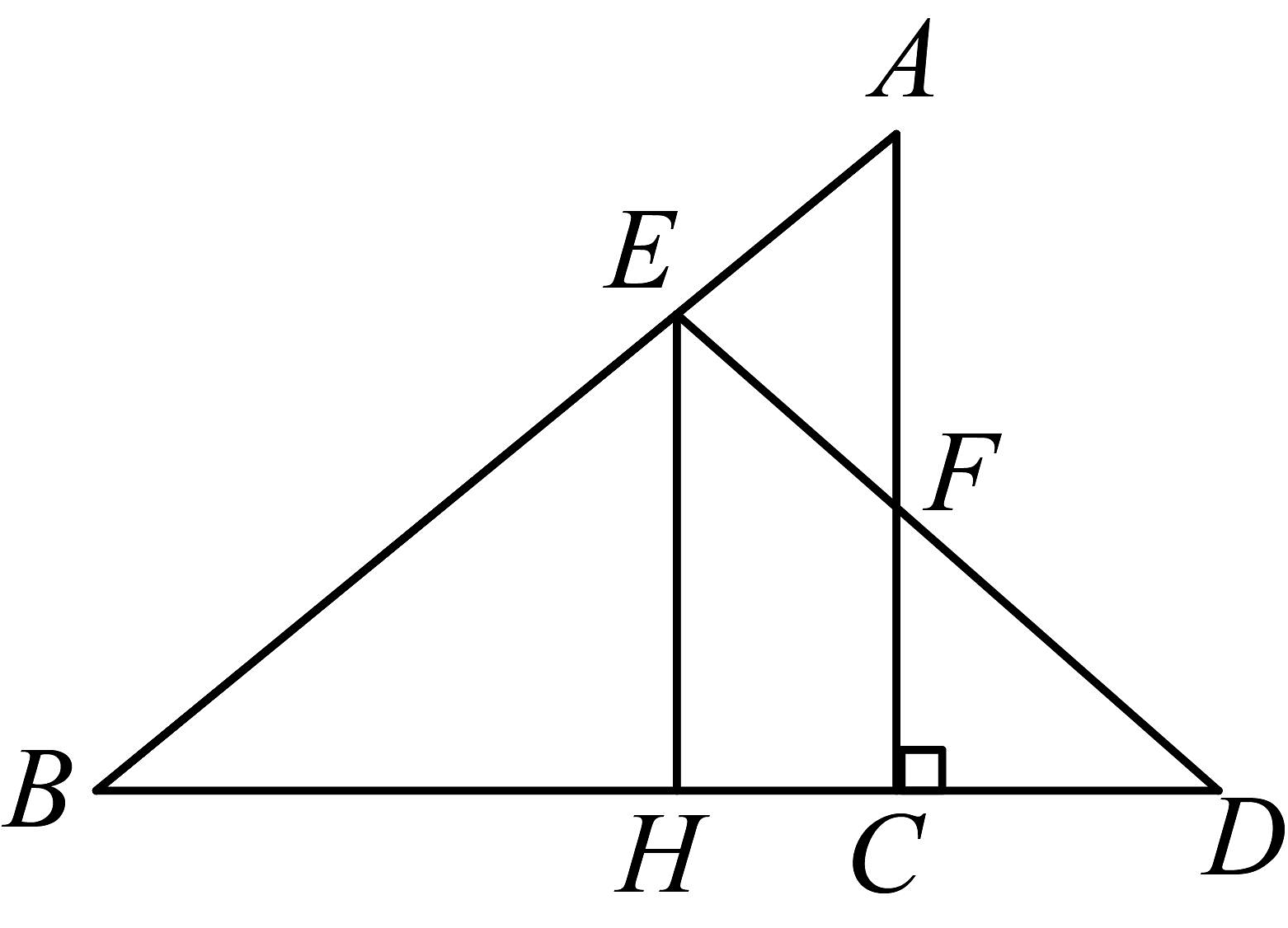
4、如图,已知D为边延长线上一点,于F交于E, , , 求的度数.

-
5、如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=6,则PD= .

-
6、如图,在 中, , , 的垂直平分线交 于点 , 的垂直平分线交 于点 , 则 度.

-
7、如图,要测量河两岸相对两点、间的距离,先在过点的的垂线上取两点、 , 使 , 再在过点的垂线上取点 , 使、、三点在一条直线上,可证明 , 所以测得的长就是、两点间的距离,这里判定的理由是 .

-
8、如图,在中,是角平分线,于点 , 的面积为15, , , 则的长是( )
 A、3 B、4 C、5 D、2
A、3 B、4 C、5 D、2 -
9、数学课上,同学们探讨利用不同画图工具画角的平分线的方法,小旭说:我用两块含的直角三角板就可以画角平分线,如图,取 , 把直角三角板按如图所示的位置放置,两直角边交于点 , 则射线是的平分线,小旭这样画的理论依据是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、如图,在中,、分别平分、 . 若 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、已知点 , 点与点关于轴对称,则点的坐标是( )A、 B、 C、 D、
-
12、已知一个三角形的两边长分别是8cm和5cm,则其第三边的长可以是( )A、1cm B、2cm C、3cm D、4cm
-
13、我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )A、7,8,9 B、4,5,6 C、5,12,13 D、8,9,10
-
14、如图,在中, , 点P从点C出发,以每秒3个单位长度的速度沿折线运动.设点P的运动时间为 .
 (1)、 .(2)、求斜边上的高线长.(3)、①当P在上时,的长为 , t的取值范围是 . (用含t的代数式表示)
(1)、 .(2)、求斜边上的高线长.(3)、①当P在上时,的长为 , t的取值范围是 . (用含t的代数式表示)②若点P在的角平分线上,则t的值为 .
(4)、在整个运动过程中,直接写出是以为一腰的等腰三角形时t的值. -
15、如图,在中,于点 , 于点 .
 (1)、如图1,若 , 求证:;(2)、如图2,点为边上的中点,连接、、 , 试判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 求的周长.
(1)、如图1,若 , 求证:;(2)、如图2,点为边上的中点,连接、、 , 试判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 求的周长. -
16、已知:方格纸中的每个小方格都是边长为个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点的坐标为 .
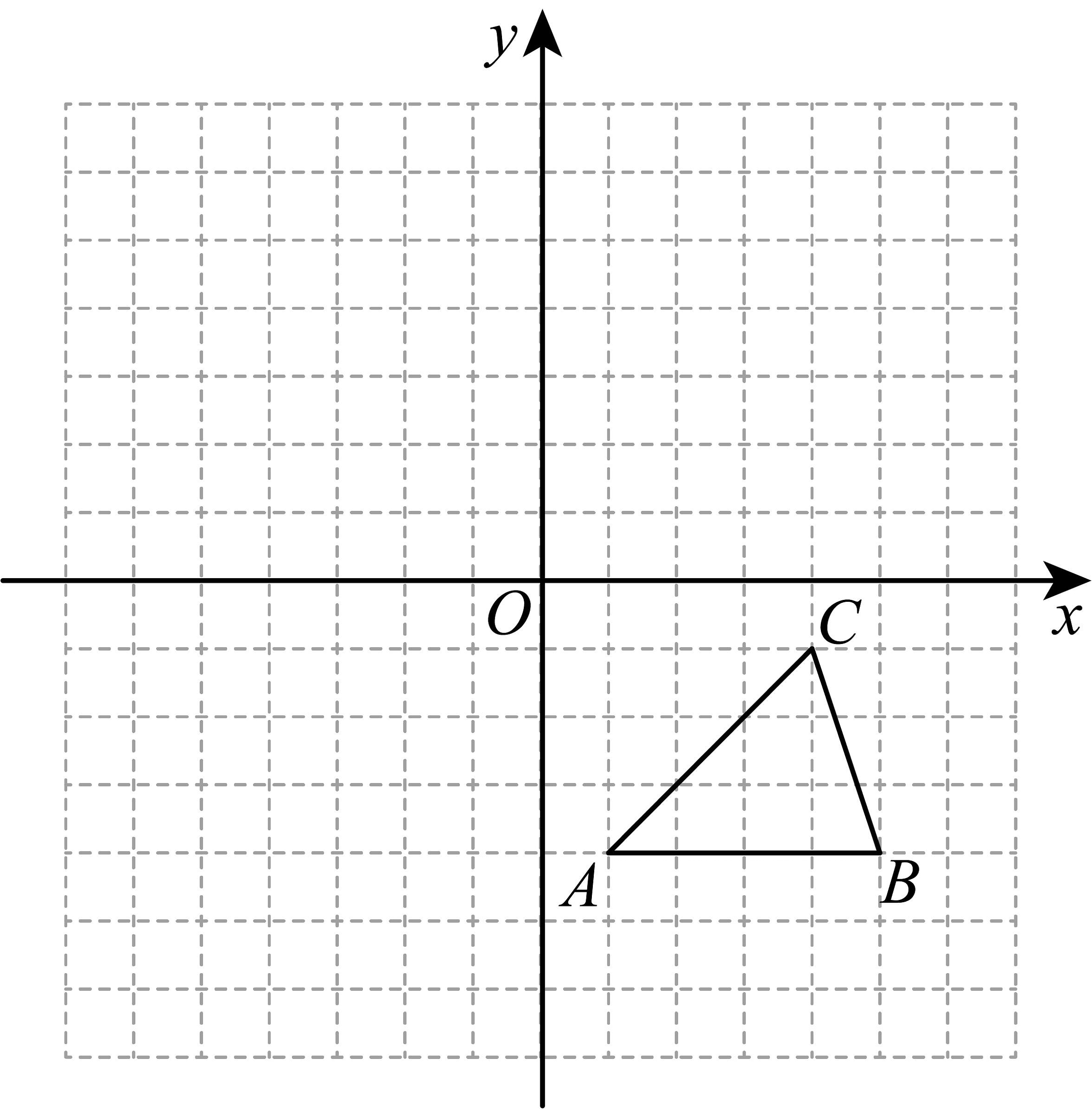 (1)、请以轴为对称轴,画出与对称的;(2)、点与点关于轴对称,则 , .(3)、如果要使与全等,那么点的坐标是 .
(1)、请以轴为对称轴,画出与对称的;(2)、点与点关于轴对称,则 , .(3)、如果要使与全等,那么点的坐标是 . -
17、解下列不等式(组),并在数轴上表示出来:(1)、;(2)、 .
-
18、将点向左平移2个单位,向下平移3个单位,后得到点 , 则平移后点的坐标 .
-
19、下列命题中,是假命题的是( )A、直角三角形的两个锐角互余 B、全等三角形的对应边相等 C、两边及其中一边的对角分别相等的两个三角形全等 D、对顶角相等
-
20、如图1是一座圆弧型拱桥侧面示意图.水面宽与桥长均为24米,桥拱顶部离水面的距离为8米,以桥拱顶部为原点,桥面为x轴建立平面直角坐标系.
 (1)、求圆弧型桥拱所在圆的半径;(2)、如图2,桥面上方有3根高度均为4米的支柱 , , , 过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面的距离为1米.
(1)、求圆弧型桥拱所在圆的半径;(2)、如图2,桥面上方有3根高度均为4米的支柱 , , , 过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面的距离为1米.①求出轴右侧一条钢缆抛物线的函数表达式;
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求经过钢缆最低点的彩带的长度.