-
1、已知a+b+c=0,则a,b,c这三个数在数轴上的对应点的位置不可能是( )A、
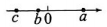 B、
B、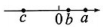 C、
C、 D、
D、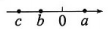
-
2、如图,数轴上一点A向左移动2个单位长度到达点B,再向右移动5个单位长度到达点C.若点A表示的数为1,则点C表示的数为( )
 A、5 B、4 C、3 D、-1
A、5 B、4 C、3 D、-1 -
3、运用分类讨论的方法解方程:|x-3|-3|x+2|=x-9.
-
4、阅读所给材料,解决问题:
分类讨论方法是求解含绝对值的一元一次方程的常用方法.例如,解方程|x-2|=3时,我们需要讨论x-2的正负性,当x-2≥0时,原方程可化为x-2=3,解得x=5;当x-2<0时,原方程可化为-(x-2)=3,即2-x=3,解得x=-1.故原方程的解为x=5或x=-1.
(1)、解方程:(2)、若关于x的方程|x+3|-1=-2m+3只有1个解,求该方程的解及m的值. -
5、如图,数轴上依次有 A,B,C三点,分别表示数a,b,c,并且满足( |c-5|=0.两只小蚂蚁 P,Q分别从A,C两点同时出发相向而行,蚂蚁 P 的速度为 3个单位长度/s,蚂蚁Q的速度为5个单位长度/s,设蚂蚁爬行的时间为ts.
 (1)、求A,B,C三点表示的数分别为多少;(2)、爬行几秒后,蚂蚁 P,Q到点 B 的距离相等?
(1)、求A,B,C三点表示的数分别为多少;(2)、爬行几秒后,蚂蚁 P,Q到点 B 的距离相等? -
6、解关于x的方程:|||x-3.5|-2.5|-1.5|=0.5.
-
7、解关于x的方程:||x+3|-k|=2.
-
8、解下列方程:(1)、|2x-3|-5=0;(2)、|x+3|=|1-2x|.
-
9、根据绝对值的定义,若|x|=4,则x=±4;若|y|=a,则y=±a.我们可以根据这样的结论,解一些简单的含绝对值的方程,例如,|2x+4|=5.
解:方程|2x+4|=5可化为2x+4=5或2x+4=-5.
当2x+4=5时,则有2x=1,解得 当2x+4=-5时,则有2x=-9,解得
故方程|2x+4|=5的解为 或
(1)、解方程:|3x-2|=4;(2)、已知|a+b+4|=16,求|a+b|的值;(3)、在(2)的条件下,若a,b都是整数,则a·b的最大值是. -
10、对于任意有理数a,b,定义运算:a⊙b=a(a+b)-1,等式右边是通常的加法、减法、乘法运算.例如,2⊙5=2×(2+5)-1=13.(1)、求(1⊙2)⊙3(2)、对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n=.(用含m,n的式子表示)
-
11、对于正数x,规定利用以上的规律计算:.
-
12、已知: , 观察上面的计算过程,利用规律计算的值为( )A、42 B、210 C、840 D、2520
-
13、对于正整数n,定义其中f(n)表示N的首位数字与末位数字的平方和,例如,规定(k为正整数),例如, , 按此定义, , .
-
14、有理数a,b在数轴上的对应点的位置如图所示.
 (1)、用“<”连接0,-a,-b,-1;(2)、化简:(3)、若 且c+b>0,求· 的值.
(1)、用“<”连接0,-a,-b,-1;(2)、化简:(3)、若 且c+b>0,求· 的值. -
15、已知有理数a,b,c在数轴上的位置如图所示,化简:|a+c|-|b-a|-2|a-c|+3|b-c|=.

-
16、有理数a,b,c在数轴上的位置如图所示,其中b,c到原点的距离相等,下列式子正确的是( )
 A、a+c>0 B、a+b>0 C、|a-c|-|b-c|>0 D、a-b<0
A、a+c>0 B、a+b>0 C、|a-c|-|b-c|>0 D、a-b<0 -
17、如图,用点A,B,C分别表示有理数a,b,c.
 (1)、判断下列各式的符号:a+b0;c-b0;c-a0.(填“>”或“<”)(2)、化简:|a+b|-|c-b|-|c-a|.
(1)、判断下列各式的符号:a+b0;c-b0;c-a0.(填“>”或“<”)(2)、化简:|a+b|-|c-b|-|c-a|. -
18、若正整数a,b分别满足 , 则ba= ( )A、4 B、8 C、9 D、16
-
19、【阅读理解】
即
的整数部分是1,小数部分是
【解决问题】
已知a是 的整数部分,b是 的小数部分,求( 的平方根.
-
20、比较大小:(1)、和(2)、和123;(3)、和0.6.