相关试卷

1、计算： ${- 1}^{6} - (0.5 - \frac{2}{3}) \div \frac{1}{3} \times [- 2 - {(- 3)}^{3}] - ∣ \frac{1}{8} - 0 . 5^{2} ∣ .$

查看解析
2、小东在解一元一次方程时，发现这样一种特殊现象：
方程 $x + \frac{1}{2} = 0$ 的解为 $x = - \frac{1}{2},$ 而 $- \frac{1}{2} = \frac{1}{2} - 1;$ 方程 $2 x + \frac{4}{3} = 0$ 的解为 $x = - \frac{2}{3},$ 而 $- \frac{2}{3} = \frac{4}{3} - 2 .$
于是，小东将这种类型的方程作如下定义：
若一个关于x的方程ax+b=0(a≠0)的解为x=b-a，则称之为“奇异方程”.请和小东一起进行以下探究：

(1)、当a=-1时，有符合要求的“奇异方程”吗?若有，请求出该方程的解；若没有，请说明理由.

(2)、若关于x的方程 ax+b=0(a≠0)为“奇异方程”，解关于 y 的方程a(a-b)y+2= $(b + \frac{1}{2}) y .$

查看解析
3、定义：对于一个有理数x，我们把[x]称作x的对称数.若x≥0，则[x]=x-2；若x<0，则[x]=x+2.例如：[1]=1-2=-1，[-2]=-2+2=0.

(1)、求 $[\frac{3}{2}], [- 1]$ 的值；

(2)、已知有理数a>0，b<0，且满足[a]=[b]，试求式子( ${(b - a)}^{3} - 2 a + 2 b$ 的值；

(3)、解方程：[2x]+[x+1]=1.

查看解析
4、对于两个不相等的有理数m，n，规定： min{m，n}表示m，n 中较小的数.例如min{3，-2}=-2，则方程 min{x，-1}=2(1-x)的解是 ( )

A、 $x = \frac{2}{3}$ 或 $x = \frac{3}{2}$ B、 $x = \frac{3}{2}$ C、 $x = \frac{2}{3}$ D、 $x = \frac{2}{3}$ 或x=-1

查看解析
5、对于任意有理数a，b，规定一种新运算“*”，使a*b=3a-2b.例如：5*(-3)=3×5-2×(-3)=21.若(2x-1)*(x-2)=-3，则x的值为( )

A、-3 B、3 C、-1 D、1

查看解析
6、定义：如果两个一元一次方程的解的和为1，那么我们就称这两个方程是“美好方程”.例如：方程2x-1=3与方程x+1=0是“美好方程”.

(1)、请判断方程4x-(x+5)=1与方程-2y-y=3是否是“美好方程”；

(2)、若关于x的方程 $\frac{x}{2} + m = 0$ 与方程3x-2=x+4是“美好方程”，求m的值；

(3)、若关于x的方程 $\frac{1}{2022} x + 1 = 3 x + k$ 与方程 $\frac{1}{2022} x - 1 = 0$ 是“美好方程”，求关于 y 的方程 $\frac{1}{2022} (y + 2) + 1 = 3 y + k + 6$ 的解.

查看解析
7、如图，现有两摞规格相同的数学课本整齐地叠放在讲台上，请根据图中给出的数据信息，解答下列问题：

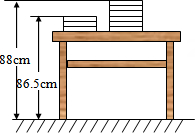(1)、每本数学课本的厚度为cm，讲台的高度为cm；

(2)、当有x本数学课本时，以同样方式叠放在讲台上，高出地面的高度为(用含x的代数式表示)；

(3)、讲台上有55本数学课本，整齐地叠放成一摞，若有16名同学各从中取走1本，求余下的数学课本高出地面的高度.

查看解析
8、

(1)、定义：若a>0，b>0，则称) $\frac{2}{\frac{1}{a} + \frac{1}{b}}$ 为a，b的调和平均数.下列表述 $\frac{2}{\frac{1}{a} + \frac{1}{b}}$ 实际意义的例子中，正确的是(填序号).
①一辆汽车以a km/h 的速度由甲地开往乙地，然后以b km/h的速度返回，汽车往返两地的平均速度；
②两杯相同质量的糖水，甲杯含糖率为a，乙杯含糖率为b，将两杯糖水混合后的含糖率；
③用相等的费用购进甲、乙两种不同的糖果，甲种糖果的单价为每千克a元，乙种糖果的单价为每千克b元，将甲、乙两种糖果混合成什锦糖果，这种什锦糖果每千克的成本价.

(2)、甲、乙两港口相距10 km，一艘游轮从甲港口顺水航行到乙港口需要a h，从乙港口逆水航行到甲港口需要 bh.问：这艘游轮以静水中的速度从甲港口航行到乙港口需要多少小时?

查看解析
9、如图，长为y、宽为x的大长方形被分割为7小块，除阴影A，B外，其余5块是形状、大小完全相同的小长方形，已知小长方形的宽为3.有下列结论：
①小长方形的长为y-9；
②阴影B的宽为x-y-9；
③阴影 A 的周长与阴影B的周长之和随y值的变化而变化；
④(y—9)(x—6)+9(x—y+9)= xy—15(y—9).
其中正确的结论有.(填序号)

查看解析
10、某工厂原计划a天完成b件产品，由于情况发生变化，要求提前x天完成任务，则现在平均每天要比原计划平均每天多生产件产品.

查看解析
11、小明心里想好了一个两位数，他将十位上的数字乘2，然后加3，再将结果乘5，最后再加上个位上的数字，最终结果是93，小明心里想的那个两位数是( )

A、78 B、87 C、23 D、12

查看解析
12、如图，空白部分的面积表示错误的为( )

A、2x B、 $x (x + 2) - x^{2}$ C、2(x+3)-6 D、(x+3)(x+2)

查看解析
13、某房屋的建筑平面图如图所示，主卧的面积为m² ，次卧的面积为m² ，客厅的面积为m²(用含有a，b的代数式表示).

查看解析
14、解方程： $x + \frac{x}{1 + 2} + \frac{x}{1 + 2 + 3} + \dots + \frac{x}{1 + 2 + 3 + \dots + 2023} = 2023 .$

查看解析
15、解方程： $\frac{1}{2} + \frac{3}{5} x - \frac{1}{6} - \frac{1}{12} - \frac{1}{20} - \frac{1}{30} - \frac{1}{42} - \frac{1}{56} - \frac{1}{72} - \frac{1}{90} - \frac{1}{110} = 1 \frac{2}{11} .$

查看解析
16、方程 $\frac{x}{3} + \frac{x}{15} + \frac{x}{35} + \dots + \frac{x}{2021 \times 2023} =$ 1的解是x=( )

A、 $\frac{1010}{1011}$ B、 $\frac{1011}{1010}$ C、 $\frac{2023}{1011}$ D、 $\frac{1011}{2023}$

查看解析
17、解方程： $\frac{x}{1 \times 2} + \frac{x}{2 \times 3} + \frac{x}{3 \times 4} + \frac{x}{4 \times 5} + \dots + \frac{x}{2022 \times 2023} = 2022 .$

查看解析
18、

(1)、已知m是常数，若式子|x-1|+|x-5|+|x-m|的最小值是6，求m的值；

(2)、已知(|x+1|+|x-3|)(|y-2|+|y+3|)=20，求x+y的最大值.

查看解析
19、在数轴上点 A 表示数a，点B 表示数b，点C表示数c，b是最小的正整数，且a，c满足 $∣ a + 2 ∣ + {(c - 7)}^{2} = 0 . P$ 是数轴上一动点，点 P 表示的数是x，当PA+PB+PC=10时，求x的值.

查看解析
20、已知数轴上A，O，B三点对应的数分别为—3，0，1，P为数轴上任意一点，其表示的数为x.

(1)、如果点 P 到点A，B的距离相等，那么x=；

(2)、若点 P到点A，B的距离之和最小，则x的取值范围是；

(3)、若点 P 到点A，O，B的距离之和最小，则最小距离是；

(4)、当点 P 到点A，B的距离之和是6时，求x的值.

查看解析

上一页 105 106 107 108 109 下一页跳转