相关试卷

1、由8根火柴棒搭成1个正方形（如图），你能移动火柴棒（不减少火柴棒总数），使得新图形的面积为这个正方形面积的一半吗？

查看解析
2、如图，大小完全相同的两个直角三角形纸片，若将它们的某条边重合，能拼成几种不同形状的平面图形? 试一试，画出拼成的图形．

查看解析
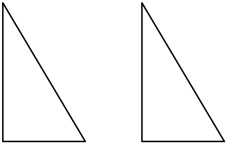
3、有一种“抢 $30$ ”的游戏，规则是：甲先说“ $1$ ”或“ $1$ ， $2$ ”，当甲先说“ $1$ ”时，乙接着说“ $2$ ”或“ $2$ ， $3$ ”；当甲先说“ $1$ ， $2$ ”时，乙接着说“ $3$ ”或“ $3$ ， $4$ ”，然后甲再接着按次序往下说一个或两个数，这样两个人反复轮流，每次每人说一个或两个数都可以，但不可以连说三个数，谁先抢到 $30$ ，谁就获胜．那么采取适当策略，其结果是胜．（填“甲”或“乙”）

查看解析
4、将一根绳子两端分别涂上红色和白色，再在中间随意画3个圆点，涂上白色或红色，然后在这三个圆点处把绳子剪断，这样所得到的各小段两端都有颜色，则两端颜色不同的小段数目一定是（填奇数或偶数）．

查看解析
5、小敏中午放学回家自己煮面条吃．有下面几道工序：①洗锅盛水 $2 m i n$ ；②洗菜 $3 m i n$ ；③准备面条及佐料 $2 m i n$ ；④用锅把水烧开 $7 m i n$ ；⑤用烧开的水煮面条和菜要 $3 m i n$ ．以上各道工序，除④外，一次只能进行一道工序．小敏要将面条煮好，最少需要 $m i n$ ．

查看解析
6、春秋时代，人们用算筹摆放图形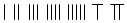，来表示1、2、3、4、5、6、7，你认为他们会用图来表示“8”，用图来表示“9”.

查看解析
7、晓明从甲地到乙地用了2.3小时，他早上8：00出发，到达时间是点分．

查看解析
8、如图，在一块木板上钉上九颗钉子，每行和每列的距离都是一样的，以钉子为顶点拉上橡皮筋可以组成正方形，这样做组成的正方形的个数是（）

A、5个 B、6个 C、4个 D、7个

查看解析
9、时间一去不复返，孩子们，转眼间，我们已经在小学阶段学习了大约2000（）

A、时 B、日 C、月 D、年

查看解析
10、小琳买了一双鞋号为“35”的鞋，但她不知道“35”的意义，你认为鞋马为“35”表示的意义是（）

A、鞋的宽度 B、鞋的高度 C、鞋的厚度 D、鞋的长度

查看解析
11、阅读下列材料：
将 $x^{2} + 2 x - 35$ 分解因式，我们可以按下面的方法解答：
解：步骤：①竖分二次项与常数项： $x^{2} = x \cdot x$ ， $- 35 = (- 5) \times (+ 7)$ ．
②交叉相乘，验中项： $\begin{array}{l} x - 5 \\ x + 7 \end{array}$ $\Rightarrow 7 x - 5 x = 2 x$ ．
③横向写出两因式： $x^{2} + 2 x - 35 = (x + 7) (x - 5)$ ．
我们将这种用十字交叉相乘分解因式的方法叫做十字相乘法．
试用上述方法分解因式：

(1)、 $x^{2} + 5 x + 4$ ；

(2)、 $x^{2} - 6 x - 7$ ；

(3)、 $2 x^{2} + x - 6$ ．

查看解析
12、一次随堂练习，珍珍做了如下四道因式分解题：
① $x^{2} - y^{2} = (x + y) (x - y)$ ；
② $a^{3} - a = a (a^{2} - 1)$ ；
③ $x^{2} y - x y^{2} = x y (x - y)$ ；
④ $2 a^{2} - 4 a b + 2 b^{2} = {(2 a + 2 b)}^{2}$ ．

(1)、珍珍做错的或不完整的题目是（填序号）；

(2)、请写出（1）题中标记做错或不完整题目的正确解题过程．

查看解析
13、先阅读材料，再回答问题：
分解因式： ${(a - b)}^{2} - 2 (a - b) + 1$ ．
解：将“ $a - b$ ”看成整体，令 $a - b = M$ ，则原式 $= M^{2} - 2 M + 1 = {(M - 1)}^{2}$ ，再将 $a - b = M$ 还原，得到：原式 $= {(a - b - 1)}^{2}$ ．
上述解题过程中用到了“整体思想”，它是数学中常用的一种思想．请你用整体思想解决下列问题：

(1)、因式分解： $9 + 6 (x + y) + {(x + y)}^{2} =$ ；

(2)、因式分解： $x^{2} - 2 x y + y^{2} - z^{2}$ ；

(3)、若 $n$ 为正整数，则 $(n + 2) (n + 3) (n^{2} + 5 n) + 9$ 的值为某一个正整数的平方．请说明理由．

查看解析
14、如图，四边形 $A B C D$ 与四边形 $D E F G$ 都是正方形，设 $A B = a$ ， $D E = b (a > b)$ ．

(1)、写出 $A G$ 的长度（用含字母a、b的代数式表示）；

(2)、观察图形，试用不同的方法表示图形中阴影部分的面积，你能获得相应的一个因式分解公式吗？请将这个公式写出来；

(3)、如果正方形 $A B C D$ 的边长比正方形 $D E F G$ 的边长多 $16 c m$ ，它们的面积相差 $960 c m^{2}$ ．试利用（2）中的公式，求a、b的值．

查看解析
15、若多项式 $x^{a} - y^{2}$ （其中 $1 \leq a \leq 6$ ，且 $a$ 为整数）能够利用平方差公式进行因式分解，则 $a$ 的值可能有几种．

查看解析
16、请利用拆项法分解因式完成下列题目：

(1)、 $a^{2} - b^{2} + 2 a + 6 b - 8$ ；

(2)、 $x^{4} - 23 x^{2} + 1$ ．

查看解析
17、分解因式：

(1)、 $- 4 x^{2} y + 4 x y^{2} - y^{3}$ ；

(2)、 $m^{2} (a - b) + 4 n^{2} (b - a)$ ．

查看解析
18、计算：

(1)、 $(3 x + 4) (3 x - 4) - (2 x + 3) (3 x - 2)$ ；

(2)、因式分解 $6 p (p + q) - 4 q (p + q)$ ．

查看解析
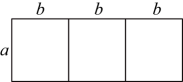
19、如图，将三个边长分别为a ， b的小长方形组成一个大长方形，已知大长方形的周长为12，面积为7．则代数式 $a^{3} b + 6 a^{2} b^{2} + 9 a b^{3}$ 的值是．

查看解析
20、因式分解：

(1)、 $a^{3} - a =$ $.$

(2)、 $- 9 + 6 x - x^{2} =$ ．

查看解析

上一页 58 59 60 61 62 下一页跳转