-
1、在计算两个数减法: , 由于不小心,减数被墨水污染;(1)、嘉淇误将后面的“”看成了“”,从而算得结果为 , 请求出被墨水污染的减数;(2)、请你正确计算此道题.
-
2、根据题意计算求值(1)、若 , , 且 ,求的值.(2)、若 , 求的值.
-
3、一只蚂蚁从某点P出发在一条直线上来回爬行,假定向右爬行的路程为主,向左爬行的路程记为负,爬行的各段路程一次为(单位:厘米): , , , , , ,(1)、蚂蚁共爬行了多少厘米?(2)、若蚂蚁共用了9分钟完成上面的路程,蚂蚁的速度是多少?
-
4、一架直升机在空中做升降练习,第一次上升210米,第二次下降232米,请问此时飞机是否又回到了原来的高度?如果没有,比原来升高了还是比原来降低了?
-
5、把下列各数填在相应的括号里.
, , , , , , , , ,
整数集合:{ …}
负分数集合:{ …}
非负有理数集合:{ …}
-
6、计算: .
-
7、计算:(1)、;(2)、;(3)、;(4)、 .
-
8、将八进制数转换成十进制数的算式为:(注: , 类似的,将二进制数转换成十进制的数为 .
-
9、某公司为了确保安全,信息需要加密传输.规则如下:加密后是 . 加密后是;加密后 .
-
10、一个点到原点的距离是2个单位长度,另一个点到原点的距离是3个单位长度,这两个点分别在原点的两侧,则这两个点表示的有理数的和是 .
-
11、若 , 则 , .
-
12、下列各数中,与880万最接近的是( )A、8801000 B、9000000 C、8891000 D、8008888
-
13、 保留一位小数是( )A、 B、 C、
-
14、下列运算中,结果为负的是( )A、 B、 C、 D、
-
15、已知有理数在数轴上的位置如图所示,则下列四个结论中正确的个数是( )
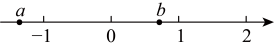
①;②;③;④
A、1 B、2 C、3 D、4 -
16、某品牌乒乓球的产品参数中标乒乓球的直径是“” , 则下列乒乓球中合格的有( )A、 B、 C、 D、
-
17、四个有理数 , , , , 其中最小的数是( )A、 B、 C、 D、
-
18、在 , 0, , 中,正数的个数为( )A、1个 B、2个 C、3个 D、4个
-
19、【教材呈现】“整体思想”是数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.下题是华师版七年级上册数学教材第120页的部分内容.
代数式的值为7,则代数式的值为____.
【阅读理解】小明在做作业时采用的方法如下:由题意得,则有 , , 所以代数式的值为5.
(1)、【方法运用】若代数式的值为15,求代数式的值.
(2)、若时,代数式的值为19,当时,求代数式的值.(3)、【拓展应用】若 , . 则的值为 .
-
20、如图是一长方形空地,长为米,宽为3b米.现准备在这个长方形空地的四个角分别修建半径为米的扇形花圃(阴影部分),中间修一条长为米,宽为米的小路,除花圃和小路外的地方都是绿地.
 (1)、四个花圃的总面积为平方米;(2)、求绿地的面积;(3)、当 , 时,求绿地的面积.
(1)、四个花圃的总面积为平方米;(2)、求绿地的面积;(3)、当 , 时,求绿地的面积.