-
1、计算题:(1)、 )(2)、 .
-
2、已知关于 的绝对值方程 有三个解,则 .
-
3、若 为整数,且 ,则 .
-
4、老师规定 表示大于 的最小整数,如: , ,则下列结论中正确的有(填序号).
① ② 的最小值是 0,
③ 的最大值是 1; ④存在有理数 ,使 成立.
-
5、如图是用黑白两种颜色的正六边形拼成的图案,按此规律,第 ( 为正整数)个图案中白色正六边形比黑色正六边形多个.(用含 的代数式表示)



第 1 个图案 第 2 个图案 第 3 个图案
-
6、若 为互不相等的正整数,且 ,则 的结果有( )A、5 种 B、6 种 C、7 种 D、8 种
-
7、 如果 ,那么 与 的大小关系是( )A、 B、 C、 D、
-
8、如图,已知数轴上点 所对应的数 都不为 0,且 是 的中点,如果 ,则原点 的大致位置在( )
 A、 的左边 B、 与 之间 C、 与 之间 D、 的右边
A、 的左边 B、 与 之间 C、 与 之间 D、 的右边 -
9、小明在某月的日历上圈出三个数 ,并求出它们的和是 42,则这三个数在日历中的位置不可能的是( )A、
 B、
B、 C、
C、 D、
D、
-
10、 如图,△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B、D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是 .

-
11、 如图,在平行四边形中,的角平分线交于点 , 的角平分线交于点 , 若 , , 则的长为 .

-
12、 若n边形的外角和为 , 则 .
-
13、 若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、且 B、 C、且 D、
-
14、 菱形和矩形都具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线平分一组对角 D、对角线互相平分并且是中心对称图形
-
15、 如果 , 则下列式子正确的是( )A、 B、 C、 D、
-
16、 在平面直角坐标系中,将点向右平移4个单位长度后的对应点的坐标是( )A、 B、 C、 D、
-
17、 下列各项变形是,是因式分解的是( )A、 B、 C、 D、
-
18、 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
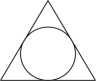 B、
B、 C、
C、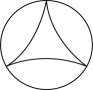 D、
D、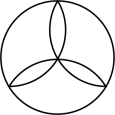
-
19、 点 是以 为直径的 上一点,过 的中点 作 于点 ,交 于点 ,连接 与 相交于点 .(1)、如图,若 也是 的直径,已知 ,求 的长.
 (2)、 如图.
(2)、 如图.
① 求证: ;
② 若 ,求 的值.
-
20、 已知二次函数 ,记该函数在 上的最大值为 ,最小值为 ,已知 .(1)、当 时,求 的值;(2)、当 时,求 的值;(3)、已知 ( 为整数),若 为整数,求 的值.