浙教版数学八年级上册期中模拟试卷一(范围:1-2章)
试卷更新日期:2025-09-23 类型:期中考试
一、选择题(本大题有10个小题,每小题3分,共 30分)
-
1. 2024年巴黎奥运会中国体育代表团取得了40金27银24铜的优异成绩,下列巴黎运动会体育图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 自行车支架一般都会采用如图△ABC的设计,这种方法应用的几何原理是( )
2. 自行车支架一般都会采用如图△ABC的设计,这种方法应用的几何原理是( ) A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、三角形的稳定性3. 如图,在△ABC中,∠ABC=90°,DE⊥AB 于点 E,交AC 于点 F,且DE=AB=4,连接BD,若BD=AC,BC=2,则AE的长为 ( )
A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、三角形的稳定性3. 如图,在△ABC中,∠ABC=90°,DE⊥AB 于点 E,交AC 于点 F,且DE=AB=4,连接BD,若BD=AC,BC=2,则AE的长为 ( )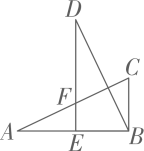 A、2 B、3 C、4 D、54. 下列不能构成直角三角形三边长的是( )A、1、2、3 B、6、8、10 C、3、4、5 D、5、12、135. 如图,在Rt中,CD是斜边AB中的中线,且 , , 则CD的长为( )
A、2 B、3 C、4 D、54. 下列不能构成直角三角形三边长的是( )A、1、2、3 B、6、8、10 C、3、4、5 D、5、12、135. 如图,在Rt中,CD是斜边AB中的中线,且 , , 则CD的长为( ) A、5 B、6 C、8 D、106. 如图,在△ABC中,∠ABC=45°,点D在AB上,点E在BC上,连接AE、CD、DE,若AE=AC=CD,CE=4,则BD的长为( )
A、5 B、6 C、8 D、106. 如图,在△ABC中,∠ABC=45°,点D在AB上,点E在BC上,连接AE、CD、DE,若AE=AC=CD,CE=4,则BD的长为( ) A、2 B、 C、4 D、7. 将等腰直角三角形纸片和长方形纸片按如下图方式叠放,若 , 则的度数为( )
A、2 B、 C、4 D、7. 将等腰直角三角形纸片和长方形纸片按如下图方式叠放,若 , 则的度数为( ) A、 B、 C、 D、8. 如图,在中, , . 通过观察尺规作图的痕迹,可以求得的度数为( ).
A、 B、 C、 D、8. 如图,在中, , . 通过观察尺规作图的痕迹,可以求得的度数为( ). A、 B、 C、 D、9. 如图,三角形纸片中,点D、E、F分别在边 , , 上,连接 , , 将、分别沿、对折,使点B、C落在点、处,若恰好平分 , 且 , 则的度数为( )
A、 B、 C、 D、9. 如图,三角形纸片中,点D、E、F分别在边 , , 上,连接 , , 将、分别沿、对折,使点B、C落在点、处,若恰好平分 , 且 , 则的度数为( ) A、 B、 C、 D、10. 将 n 个边长都为 1 的正方形按如图所示的方法摆放,点 , ···, 分别是正方形对角线的交点,则 2022 个正方形照这样重叠形成的重叠部分的面积和为( )
A、 B、 C、 D、10. 将 n 个边长都为 1 的正方形按如图所示的方法摆放,点 , ···, 分别是正方形对角线的交点,则 2022 个正方形照这样重叠形成的重叠部分的面积和为( ) A、 B、 C、1 D、2020
A、 B、 C、1 D、2020二、填空题(本题有8个小题,每小题3分,共24分)
-
11. 命题“等边三角形的三边相等”的逆命题是 , 它是命题填“真”或“假” .12. 如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为度.
 13. 如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=BD,∠ADB=90°,连接CD,若AB=2 , 则S△BCD=.
13. 如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=BD,∠ADB=90°,连接CD,若AB=2 , 则S△BCD=. 14. 如图,在中, , , 则.
14. 如图,在中, , , 则. 15. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,已知EH=EB=4,S△AEH=12,则CH的长为.
15. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,已知EH=EB=4,S△AEH=12,则CH的长为. 16. 如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OD的垂直平分线交OA、OB分别于点P,Q,点E是OA上异于点P的一点,且DE=OP=6,则△ODE的面积为.
16. 如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OD的垂直平分线交OA、OB分别于点P,Q,点E是OA上异于点P的一点,且DE=OP=6,则△ODE的面积为. 17. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .
17. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .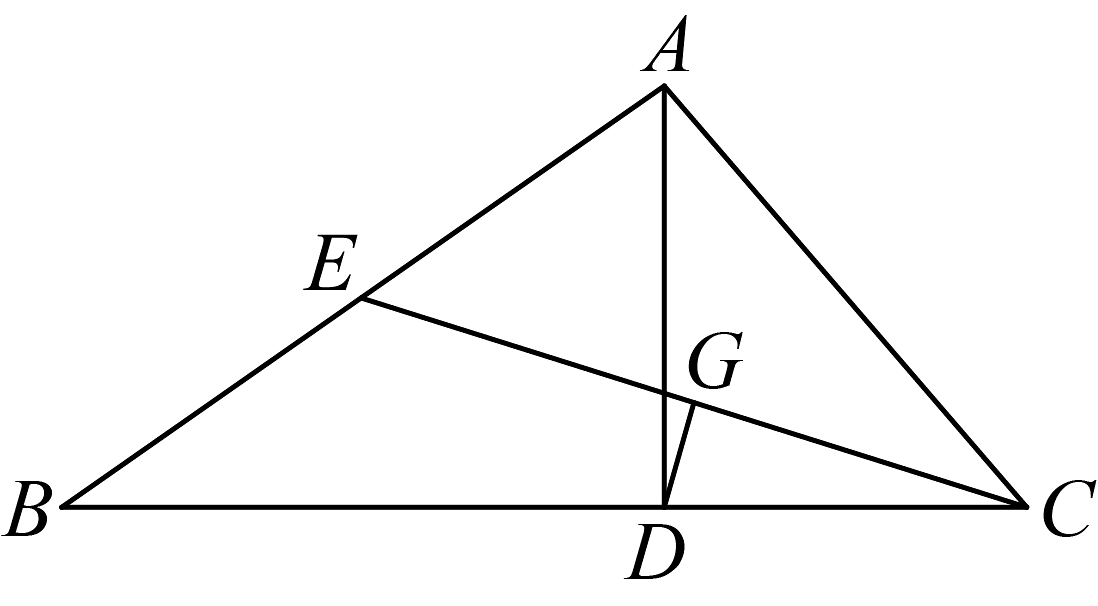 18. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 .
18. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 .
三、解答题(本题有5小题,共46分,解答应写出文字说明、证明过程或演算步骤)
-
19. 如图,在平面直角坐标系中,的顶点 , , 均在正方形网格的格点上.
 (1)、在图中画出关于轴对称的图形△;点的对应点的坐标是 ▲ ;(2)、求△的面积;(3)、在中,边上的高为 .20. 如图, 已知 是直线 上的一点, 平分 , 射线 , .
(1)、在图中画出关于轴对称的图形△;点的对应点的坐标是 ▲ ;(2)、求△的面积;(3)、在中,边上的高为 .20. 如图, 已知 是直线 上的一点, 平分 , 射线 , . (1)、 求 的度数.(2)、 若 , 说明: .21. 如图,在中, .
(1)、 求 的度数.(2)、 若 , 说明: .21. 如图,在中, . (1)、用尺规作图:作的角平分线,交于点D,作的垂直平分线,交于点P(保留痕迹,不写作法);(2)、连接 , , 试判断 , , 间的数量关系,并说明理由;(3)、若 , 求的度数.22. 在中, , , 是边上一点,连接 , , 且 , 与交于点 .
(1)、用尺规作图:作的角平分线,交于点D,作的垂直平分线,交于点P(保留痕迹,不写作法);(2)、连接 , , 试判断 , , 间的数量关系,并说明理由;(3)、若 , 求的度数.22. 在中, , , 是边上一点,连接 , , 且 , 与交于点 . (1)、求证:;(2)、当时,求证:平分 .23. 感知:如图①所示,分别以的边 , 为边向外作等边、等边 , 连接 , . 易证:(不需要证明).
(1)、求证:;(2)、当时,求证:平分 .23. 感知:如图①所示,分别以的边 , 为边向外作等边、等边 , 连接 , . 易证:(不需要证明).探究:如图②所示,点是线段上方的一个动点,分别以的边 , 为直角边向外作等腰直角、等腰直角 , 且均以点为直角顶点,连接 , .
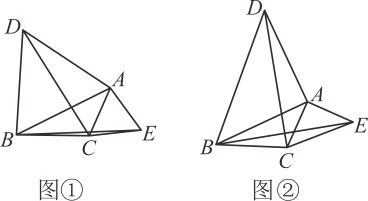 (1)、求证:;(2)、若 , , 则线段的最大值是 . (直接填答案,不需要过程)24. 如图,已知是等边三角形, , 点P从点A出发,沿射线以的速度运动,过点P作交射线于点E,同时点Q从点C出发沿的延长线以的速度运动,连接、 , 设点P的运动时间为 .
(1)、求证:;(2)、若 , , 则线段的最大值是 . (直接填答案,不需要过程)24. 如图,已知是等边三角形, , 点P从点A出发,沿射线以的速度运动,过点P作交射线于点E,同时点Q从点C出发沿的延长线以的速度运动,连接、 , 设点P的运动时间为 .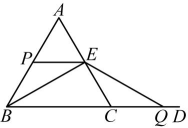 (1)、当点P在边上,且不与点、重合时,求证:;(2)、直接写出的长(用含t的代数式表示);(3)、在不添加字母和连接其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.(请写出所有的可能性)
(1)、当点P在边上,且不与点、重合时,求证:;(2)、直接写出的长(用含t的代数式表示);(3)、在不添加字母和连接其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.(请写出所有的可能性)