三角形的基础模型—浙教版数学八年级上册解题模型
试卷更新日期:2025-09-23 类型:复习试卷
一、A字模型(截角模型)
-
1. 一张三角形纸片如图所示,已知 , 若沿着虚线剪掉阴影部分纸片,记 , 则下列选项正确的是( )
 A、 B、 C、 D、无法比较α和的大小2. 如图,将纸片△ABC 沿着DE 折叠压平,则( ).
A、 B、 C、 D、无法比较α和的大小2. 如图,将纸片△ABC 沿着DE 折叠压平,则( ). A、∠A=∠1+∠2 B、 C、 D、D.3. 如图,在四边形ABCD中,点E,F分别是AD,BC上的点,将四边形ABCD沿直线 EF 折叠,若∠A=130°,∠B=110°,则∠1+∠2的度数为.
A、∠A=∠1+∠2 B、 C、 D、D.3. 如图,在四边形ABCD中,点E,F分别是AD,BC上的点,将四边形ABCD沿直线 EF 折叠,若∠A=130°,∠B=110°,则∠1+∠2的度数为. 4. 如图,在平面直角坐标系xOy中,△ABC的顶点A(0,2),B(2 , 0)分别在y轴和x轴上,AC 为△ABO 的一个外角的平分线,点 D,E 分别在 AC 和 BC 上,将△CDE 沿直线 DE 折叠使得点 C 的对应点C'落在△ABC 的内部,若∠ABC =90°,则∠ADC'+∠BEC'与∠A 的关系为 ( )
4. 如图,在平面直角坐标系xOy中,△ABC的顶点A(0,2),B(2 , 0)分别在y轴和x轴上,AC 为△ABO 的一个外角的平分线,点 D,E 分别在 AC 和 BC 上,将△CDE 沿直线 DE 折叠使得点 C 的对应点C'落在△ABC 的内部,若∠ABC =90°,则∠ADC'+∠BEC'与∠A 的关系为 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、8字模型
-
5. 一副三角板按如图所示位置放置,其中一块三角板的直角边 EF落在另一块三角板的斜边AC上,边BC与DF交于点 G,与ED交于点 H.则∠BGD 的度数为( )
 A、105° B、115° C、125° D、135°6. 如图,五角星的顶点为A,B,C,D,E,连接AC,BD,CE,DA,EB,则∠A+∠B+∠C+∠D+∠E 的度数为.
A、105° B、115° C、125° D、135°6. 如图,五角星的顶点为A,B,C,D,E,连接AC,BD,CE,DA,EB,则∠A+∠B+∠C+∠D+∠E 的度数为. 7. 如图,在△ABC中,AD是△ABC的角平分线,点F在射线AD上,FE⊥BC于点E,∠C=80°,∠B=36°,则∠F=°.
7. 如图,在△ABC中,AD是△ABC的角平分线,点F在射线AD上,FE⊥BC于点E,∠C=80°,∠B=36°,则∠F=°. 8. 如图①,已知线段AB,CD 相交于点O,连接AC,BD,我们把形如这样的图形称为“对顶三角形”.
8. 如图①,已知线段AB,CD 相交于点O,连接AC,BD,我们把形如这样的图形称为“对顶三角形”. (1)、求证:∠A+∠C=∠B+∠D.(2)、如图②,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点 P,且与CD,AB 分别相交于点M,N.
(1)、求证:∠A+∠C=∠B+∠D.(2)、如图②,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点 P,且与CD,AB 分别相交于点M,N.①以线段AC 为边的“对顶三角形”有 ▲ 个,以点O为交点的“对顶三角形”有 ▲ 个.
②若∠B=100°,∠C=120°,求∠P 的度数.
③若角平分线中角的关系改为 试探究∠P 与∠B,∠C 之间存在的数量关系,并证明理由.
三、飞镖模型
-
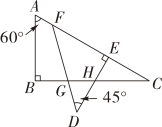
9. 如图,已知 , 于点F, , , 则的度数是( )
 A、 B、 C、 D、10. 如图是可调躺椅示意图(数据如图),AE 与 BD 的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使 , 则∠D应(填“调大”或“调小”)度.
A、 B、 C、 D、10. 如图是可调躺椅示意图(数据如图),AE 与 BD 的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使 , 则∠D应(填“调大”或“调小”)度. 11. 如图,∠ABD 与∠ACD 的角平分线交于点 P,若∠A=50°,∠D=10°,则∠P 的度数为( ).
11. 如图,∠ABD 与∠ACD 的角平分线交于点 P,若∠A=50°,∠D=10°,则∠P 的度数为( ). A、15° B、20° C、25° D、30°12. 如图,将含 30°角的直角三角板ABC 的直角∠A放入△DEF的内部,点 E,F恰好为AB,AC 的中点,若∠D =45°,∠DFE=56°,则∠DEA的度数为 ( )
A、15° B、20° C、25° D、30°12. 如图,将含 30°角的直角三角板ABC 的直角∠A放入△DEF的内部,点 E,F恰好为AB,AC 的中点,若∠D =45°,∠DFE=56°,则∠DEA的度数为 ( ) A、11° B、15° C、19° D、26°13. 如图,∠ABD,∠ACD的10等分线分别相交于点 G1 , G2 , …,G9 , 若∠BDC=125°,∠A=60°,则∠BG6C 的度数为.
A、11° B、15° C、19° D、26°13. 如图,∠ABD,∠ACD的10等分线分别相交于点 G1 , G2 , …,G9 , 若∠BDC=125°,∠A=60°,则∠BG6C 的度数为. 14. 定义:在四边形中,仅有一个角大于180°,但小于360°,这样的四边形叫做凹四边形(如图①).因为凹四边形ABOC 形似燕尾,其四角具有“∠BOC=∠A+∠B+∠C”这个规律,所以我们把这个模型叫做“燕尾”模型.
14. 定义:在四边形中,仅有一个角大于180°,但小于360°,这样的四边形叫做凹四边形(如图①).因为凹四边形ABOC 形似燕尾,其四角具有“∠BOC=∠A+∠B+∠C”这个规律,所以我们把这个模型叫做“燕尾”模型.
模型应用
(1)、如图②,求∠A+∠B+∠C+∠D+∠E+∠F的度数;(用含α的代数式表示) (2)、如图③,若∠BAC 的平分线与∠BOC 的平分线交于点 D,求证:2∠D=∠C-∠B.
(2)、如图③,若∠BAC 的平分线与∠BOC 的平分线交于点 D,求证:2∠D=∠C-∠B.
四、双内角平分线模型
-
15. 如图,把剪成三部分,边 , , 放在同一直线上,点都落在直线上,直线在中,若 , 则的度数为( )
 A、 B、 C、 D、16. 如图,在△ABC中,BO,CO分别平分∠ABC,∠ACB,若∠ABC+∠ACB=100°,则∠BOC的度数为 ( )
A、 B、 C、 D、16. 如图,在△ABC中,BO,CO分别平分∠ABC,∠ACB,若∠ABC+∠ACB=100°,则∠BOC的度数为 ( ) A、100° B、110° C、120° D、130°17. 如图①、②中, , , , 则的度数为( )
A、100° B、110° C、120° D、130°17. 如图①、②中, , , , 则的度数为( ) A、111 B、174 C、153 D、13218. 如图,在△ABC中, 若∠AED=35°,则∠C 的度数为.
A、111 B、174 C、153 D、13218. 如图,在△ABC中, 若∠AED=35°,则∠C 的度数为. 19. 问题情境:
19. 问题情境:如图1,在中,和的平分线交于点 .
 (1)、探索发现:
(1)、探索发现:若 , 则的度数为________;若 , 则的度数为________.
(2)、猜想证明:猜想与之间的数量关系,并证明你的猜想.
(3)、拓展应用:如图2,在中,和的平分线交于点 , 和的平分线交于点 , 直接写出与之间的数量关系.
五、内外角平分线模型
-
20. 如图,在△ABC 中,∠ABC=50°,∠ACB=60°,点 E 在BC 的延长线上,∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点 D,连接AD.下列结论不正确的是( ).
 A、∠BAC=70° B、∠DOC=90° C、∠BDC=35° D、21. 如图,在中, , 的平分线 , 交于点 , 为的外角的平分线,的延长线交于点 , , 则的大小为
A、∠BAC=70° B、∠DOC=90° C、∠BDC=35° D、21. 如图,在中, , 的平分线 , 交于点 , 为的外角的平分线,的延长线交于点 , , 则的大小为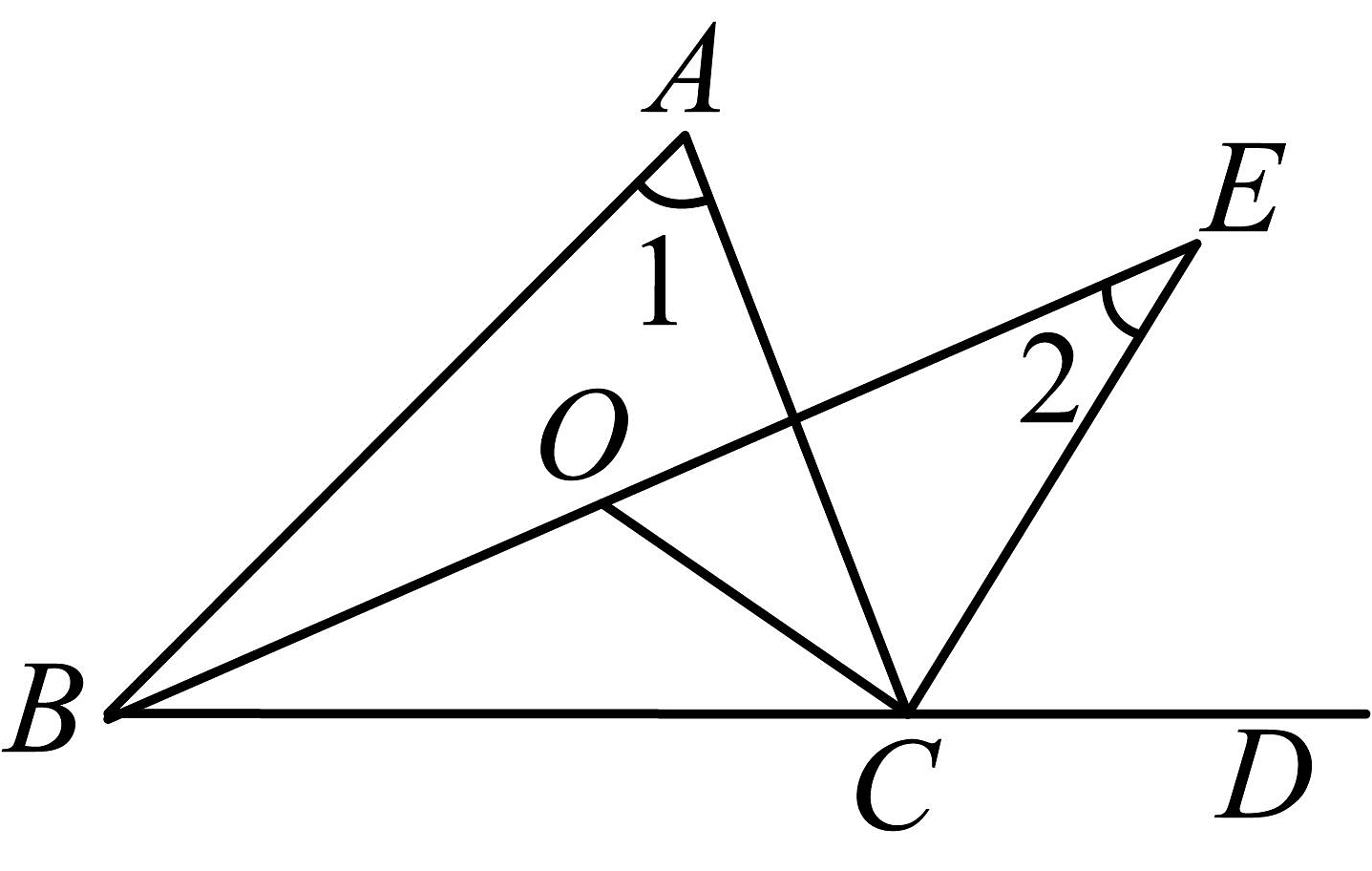 22. 如图,在△ABC中,∠A=70°,∠ABC的平分线与∠ACD的平分线交于点. 的平分线与 的平分线交于点 得 的平分线与 的平分线交于点 则 .
22. 如图,在△ABC中,∠A=70°,∠ABC的平分线与∠ACD的平分线交于点. 的平分线与 的平分线交于点 得 的平分线与 的平分线交于点 则 . 23. 如图,的角平分线交于点 , 若 , 则的度数为 .
23. 如图,的角平分线交于点 , 若 , 则的度数为 . 24. 如图,的角平分线、交于点 . 延长至 , 与的延长线相交于点 , 且 , , 若的面积为6, , 则线段的长度为 .
24. 如图,的角平分线、交于点 . 延长至 , 与的延长线相交于点 , 且 , , 若的面积为6, , 则线段的长度为 . 25. 如图
25. 如图 (1)、如图1,在△ABC中,∠ABC与∠ACB的角平分线相交于点D , BD与∠ACB的外角平分线相交于点E .
(1)、如图1,在△ABC中,∠ABC与∠ACB的角平分线相交于点D , BD与∠ACB的外角平分线相交于点E .①若∠A=80°,求∠BDC的度数;
②写出∠A与∠E之间的数量关系,并证明;
(2)、如图2,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1 , 得∠A1;∠A1BC与∠A1CD的平分线相交于点A2 , 得∠A2;…;∠A2021BC与∠A2021CD的平分线相交于点A2022 , 得∠A2022 , 直接写出∠A2022的度数 (用含x的代数式表示).六、双外角平分线模型
-
26. 如图,的外角和的平分线交于点E,和的平分线交于点M,若 , 则的度数为( )
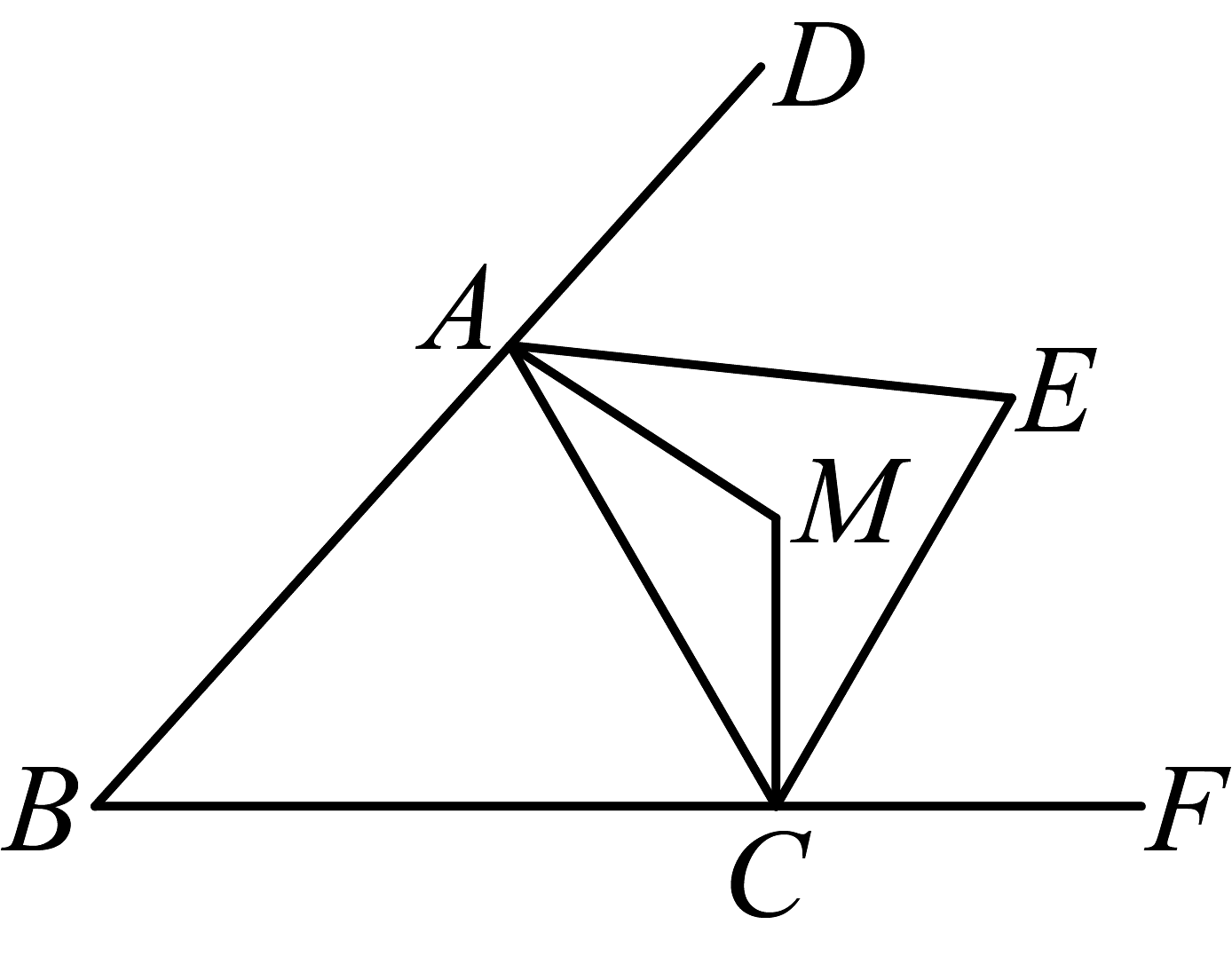 A、 B、 C、 D、27. 如图,BH是∠ABC 的平分线,BD 和CD 是△ABC两个外角的平分线,延长DC 与 BH交于点 H,若∠D =60°,∠ACB = 65°,则∠HBC的度数为 ( )
A、 B、 C、 D、27. 如图,BH是∠ABC 的平分线,BD 和CD 是△ABC两个外角的平分线,延长DC 与 BH交于点 H,若∠D =60°,∠ACB = 65°,则∠HBC的度数为 ( ) A、27.5° B、30° C、32.5° D、35°
A、27.5° B、30° C、32.5° D、35°

