鲁教版(五四制)数学七年级上学期10月月考卷(范围:第一章~第二章第二节)
试卷更新日期:2025-09-23 类型:月考试卷
一、选择题
-
1. 在美术课堂上,李老师展示了几幅艺术作品,其中属于轴对称图形的是( )A、
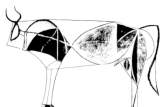 毕加索的立体主义画作《公牛》
B、
毕加索的立体主义画作《公牛》
B、 埃舍尔的《天与水》
C、
埃舍尔的《天与水》
C、 中国传统剪纸作品《连年有余》
D、
中国传统剪纸作品《连年有余》
D、 水彩画《蝶》
2. 如图,把含有60°的直角三角板斜边放在直线l上,则∠α的度数是( )
水彩画《蝶》
2. 如图,把含有60°的直角三角板斜边放在直线l上,则∠α的度数是( )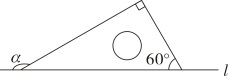 A、120 B、130° C、140° D、150°3. 如图,为估计池塘两岸A,B间的距离,小明在池塘一侧选取了一点P,测得PA=14m,PB=10m,那么AB间的距离不可能是( )
A、120 B、130° C、140° D、150°3. 如图,为估计池塘两岸A,B间的距离,小明在池塘一侧选取了一点P,测得PA=14m,PB=10m,那么AB间的距离不可能是( ) A、4m B、15m C、20m D、22m4. 如图,若△ABC≌△ADE,则下列结论中不成立的是( )
A、4m B、15m C、20m D、22m4. 如图,若△ABC≌△ADE,则下列结论中不成立的是( )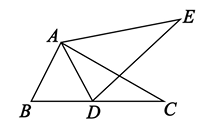 A、BC=DE B、∠BAD=∠CDE C、DA平分∠BAE D、∠CAE=∠CDE5. 油纸伞是汉族古老的传统用品之一.图1是一把油纸伞实物图,图2 为其伞骨示意图.已知 那么△AED ≌△AFD 的依据是( )
A、BC=DE B、∠BAD=∠CDE C、DA平分∠BAE D、∠CAE=∠CDE5. 油纸伞是汉族古老的传统用品之一.图1是一把油纸伞实物图,图2 为其伞骨示意图.已知 那么△AED ≌△AFD 的依据是( )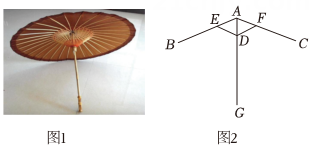 A、SSS B、ASA C、AAS D、SAS6. 如图,已知 , 添加下列条件仍无法证明的是( )
A、SSS B、ASA C、AAS D、SAS6. 如图,已知 , 添加下列条件仍无法证明的是( ) A、 B、 C、 D、7. 数学来源于生活,又服务于生活.以下四幅图中用数学原理解释不正确的是( )
A、 B、 C、 D、7. 数学来源于生活,又服务于生活.以下四幅图中用数学原理解释不正确的是( )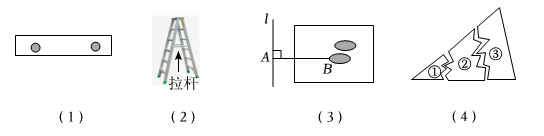 A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS8. 嘉嘉先画出了 , 再利用尺规作图画出了 , 使 . 图1~图3是其作图过程.
A、图(1)两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图(2)人字梯中间一般会设计一根“拉杆”,这样做的道理是利用了三角形的稳定性 C、图(3)体育课堂测量跳远的成绩是利用了垂线段最短 D、图(4)一块三角形模具打碎为三块,只带编号为③的那一块碎片到商店去,就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法SAS8. 嘉嘉先画出了 , 再利用尺规作图画出了 , 使 . 图1~图3是其作图过程.(1)以点为圆心,以适当长为半径画弧,交AB于点 , 交AC于点 .
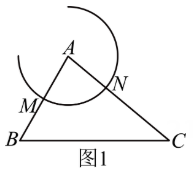
(2)以点为圆心,以MN长为半径画弧,与(1)中的弧交于点 , 作射线AP.
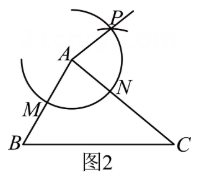
(3)以点A为圆心,先以AB长为半径画弧,与边AC交于点 , 再以AC长为半径画弧,与射线AP交于点 , 连接DE .
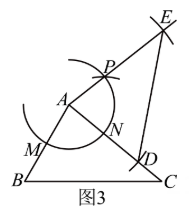
在嘉嘉的作法中,可直接判定的依据是( )
A、SSS B、SAS C、ASA D、AAS9. 将 n 个边长都为 1 的正方形按如图所示的方法摆放,点 , ···, 分别是正方形对角线的交点,则 2022 个正方形照这样重叠形成的重叠部分的面积和为( ) A、 B、 C、1 D、202010. 如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC 的平分线BE 交AD 于点 F,AG 平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论是( ).
A、 B、 C、1 D、202010. 如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC 的平分线BE 交AD 于点 F,AG 平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论是( ).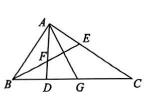 A、②③④ B、①③④ C、①②④ D、①②③
A、②③④ B、①③④ C、①②④ D、①②③二、填空题
-
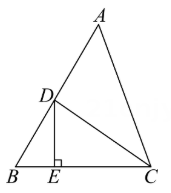
11. 如图,在△ABC中,∠A=50°,∠B=60°,CD平分∠ACB,DE⊥BC于E,则∠CDE的度数为.
 12. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC , AB于点M、N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P , 作射线AP交边BC于点D , 若CD=3,AB=10,则△ABD的面积是 .
12. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC , AB于点M、N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P , 作射线AP交边BC于点D , 若CD=3,AB=10,则△ABD的面积是 .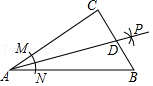 13. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则 .
13. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则 .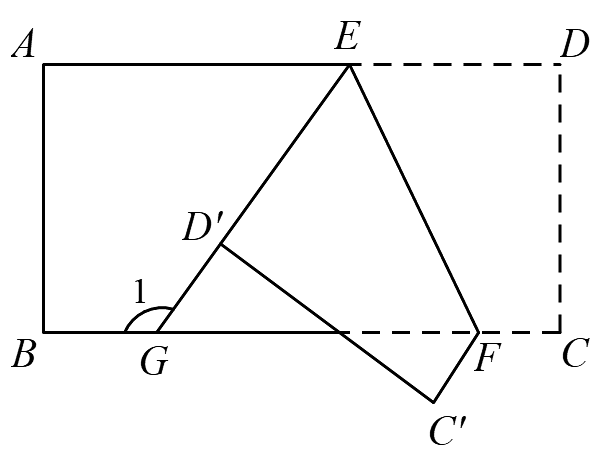 14. 如图,在锐角三角形ABC中, , BE,CD分别为的角平分线BE,CD相交于点F,FG平分 , 已知 , .的面积为2.5,的面积为.
14. 如图,在锐角三角形ABC中, , BE,CD分别为的角平分线BE,CD相交于点F,FG平分 , 已知 , .的面积为2.5,的面积为.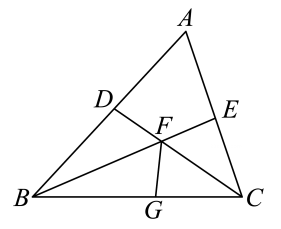 15. 如图,中, , , 。点P从A点出发沿路径运动,终点为B点;点Q从B点出发沿路径运动,终点为A点,点P和点Q分别以1cm/s和3cm/s的速度同时开始运动,两点到达相应的终点时分别停止运动.若分别过点P和Q作于E,于F. 当与全等时,点P的运动时间t为s.
15. 如图,中, , , 。点P从A点出发沿路径运动,终点为B点;点Q从B点出发沿路径运动,终点为A点,点P和点Q分别以1cm/s和3cm/s的速度同时开始运动,两点到达相应的终点时分别停止运动.若分别过点P和Q作于E,于F. 当与全等时,点P的运动时间t为s.
三、解答题
-
16. 如图,写出其中相等的角。
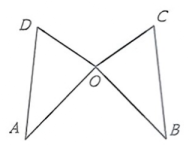 17. 如图,BE⊥AE,CF⊥AE,垂足分别为E、F,且D是BC的中点,已知DE=3,求DF的长度.
17. 如图,BE⊥AE,CF⊥AE,垂足分别为E、F,且D是BC的中点,已知DE=3,求DF的长度.
解: ∵BE⊥AE,CF⊥AE
∴∠CFD=∠E=90°
∴D为BC中点
∴ ▲
在△CDF和△BDE中
( )
∴△CDF≌△BDE( )
∴DF=DE=3( )
18. 如图所示,在中,是高,、是角平分线,它们相交于点O, , .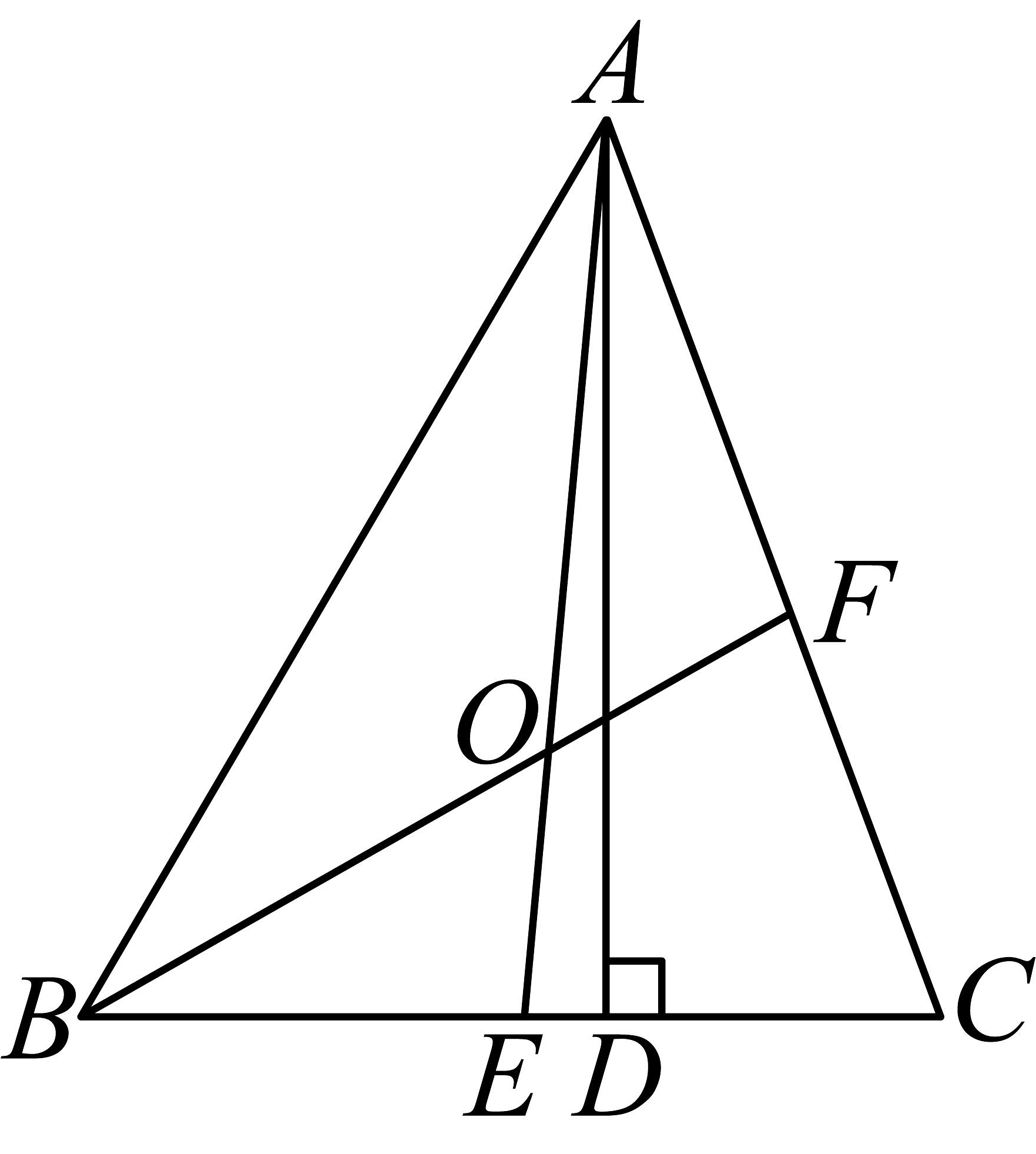 (1)、求的度数;(2)、求的度数.19. 将沿某条直线折叠,使斜边的两个端点A与B重合,折痕为 .
(1)、求的度数;(2)、求的度数.19. 将沿某条直线折叠,使斜边的两个端点A与B重合,折痕为 . (1)、如果 , , 试求的周长;(2)、如果 , 求的度数.20. 如图,已知求的度数。
(1)、如果 , , 试求的周长;(2)、如果 , 求的度数.20. 如图,已知求的度数。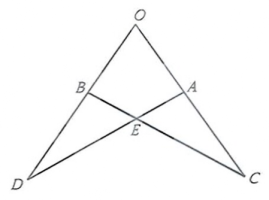 21. 如图,在四边形ABEC中,∠E和∠A都是直角,且AB=AC . 现将△BEC沿BC翻折,点E的对应点为E',BE'与AC边相交于D点,且BE'恰好是∠ABC的平分线,若CE=1,求BD的长.
21. 如图,在四边形ABEC中,∠E和∠A都是直角,且AB=AC . 现将△BEC沿BC翻折,点E的对应点为E',BE'与AC边相交于D点,且BE'恰好是∠ABC的平分线,若CE=1,求BD的长.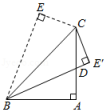 22. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题:
22. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题: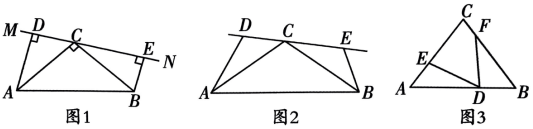 (1)、如图 1, 猜想DE,AD,BE之间的关系;(2)、如图2,将(1)中条件改为. 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点D为AB上一点, , 请直接写出AB的长.
(1)、如图 1, 猜想DE,AD,BE之间的关系;(2)、如图2,将(1)中条件改为. 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点D为AB上一点, , 请直接写出AB的长.