人教版数学八年级上学期期中仿真模拟试卷五(范围:13.1-15.3)
试卷更新日期:2025-09-23 类型:期中考试
一、选择题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各图中,作△ABC边AB上的高,正确的是 ( )A、
2. 下列各图中,作△ABC边AB上的高,正确的是 ( )A、 B、
B、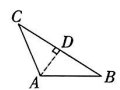 C、
C、 D、
D、 3. 如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( )
3. 如图是两个全等三角形,图中的字母表示三角形的边长,则的度数是( ) A、 B、 C、 D、4. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就画出一个与原三角形形状大小完全一样(即全等)的三角形,这两个三角形全等的依据为( )
A、 B、 C、 D、4. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就画出一个与原三角形形状大小完全一样(即全等)的三角形,这两个三角形全等的依据为( ) A、 B、 C、 D、5. 已知 , 求作射线 , 使平分 , 那么作法的合理顺序是( )
A、 B、 C、 D、5. 已知 , 求作射线 , 使平分 , 那么作法的合理顺序是( )①作射线;
②在射线和上分别截取 , 使;
③分别以D、E为圆心,大于的长为半径在内作弧,两弧交于点C.
 A、①②③ B、②①③ C、②③① D、③①②6. 如图,在 中, , 平分 , 于 , , 则的周长为( )
A、①②③ B、②①③ C、②③① D、③①②6. 如图,在 中, , 平分 , 于 , , 则的周长为( ) A、 B、 C、 D、7. 如图是某公园的一滑梯侧面图,已知 , 滑梯架的高为 , 则滑梯长为( )
A、 B、 C、 D、7. 如图是某公园的一滑梯侧面图,已知 , 滑梯架的高为 , 则滑梯长为( ) A、 B、 C、 D、8. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm9. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( )
A、 B、 C、 D、8. 下列各组线段中,首尾相接不能组成三角形的是( )A、12cm,8cm,5cm B、12cm,8cm,6cm C、12cm,5cm,6cm D、8cm,5cm,6cm9. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( ) A、①②③ B、②③④ C、①③④ D、①②④10. 如图,已知, , 点、、…在射线上,点、、在射线上,、、、均为等边三角形,若 , 则的边长为( )
A、①②③ B、②③④ C、①③④ D、①②④10. 如图,已知, , 点、、…在射线上,点、、在射线上,、、、均为等边三角形,若 , 则的边长为( ) A、16 B、32 C、64 D、128
A、16 B、32 C、64 D、128二、填空题
-
11. 如图,左边是计算器上的数字“5”,若以直线为对称轴,则它的轴对称图形是数字.
 12. 如图是一种常见的户外健身器材,其支架的三角结构运用的数学原理是
12. 如图是一种常见的户外健身器材,其支架的三角结构运用的数学原理是 13. 若点关于y轴的对称点是点 , 则 .14. 如图,在中, , 平分 . 若 , , 则 .
13. 若点关于y轴的对称点是点 , 则 .14. 如图,在中, , 平分 . 若 , , 则 .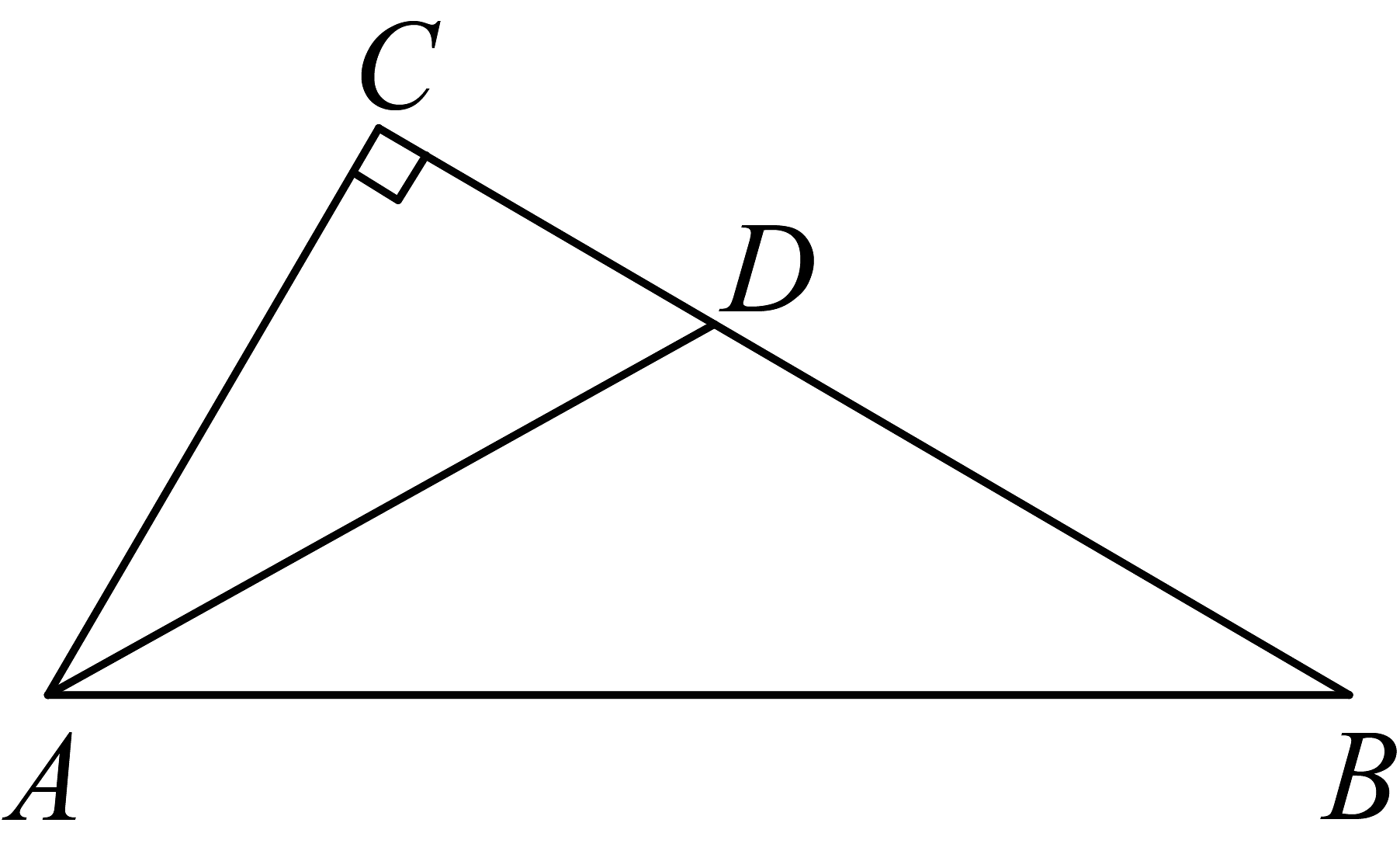 15. 如图,在等腰中, , , , 是底边上的高.在的延长线上有一个动点 , 连接 , 作 , 交的延长线于点 , 的角平分线交边于点 , 则在点运动的过程中,线段的最小值为 .
15. 如图,在等腰中, , , , 是底边上的高.在的延长线上有一个动点 , 连接 , 作 , 交的延长线于点 , 的角平分线交边于点 , 则在点运动的过程中,线段的最小值为 .
三、解答题
-
16. 如图,在Rt△ABC中,CD是斜边AB上的高线.
 (1)、CDAC.(填“<”或“>”)(2)、AC+BCAB(填“<”或“>”)(3)、若点E是线段AB上的一个动点,连结CE,则CDCE.(填“≤”或“>”)17. 对下面每个三角形,过顶点A画出中线,角平分线和高.
(1)、CDAC.(填“<”或“>”)(2)、AC+BCAB(填“<”或“>”)(3)、若点E是线段AB上的一个动点,连结CE,则CDCE.(填“≤”或“>”)17. 对下面每个三角形,过顶点A画出中线,角平分线和高. 18. 作图题:已知∠ABC及AB上一点A,
18. 作图题:已知∠ABC及AB上一点A,(1)过点A画AE⊥BC,垂足为点E,此时线段的长为点A到直线BC的距离______.
(2)尺规作图(不写作法,保留作图痕迹)在射线BC上,以C为定点,作∠FCD=∠ABC
 19. 如图,在平面直角坐标系中,点为坐标原点,已知三个顶点的坐标分别为 .
19. 如图,在平面直角坐标系中,点为坐标原点,已知三个顶点的坐标分别为 . (1)、先画出关于轴对称的 , 点 , , 关于轴的对称点分别是 , 则点的坐标为 , 点的坐标为_______;(2)、在轴上找到一点 , 使与之和最短不写作法,保留痕迹 , 则点的坐标为______.20. 如图,是的角平分线,平分 , 交于点E.
(1)、先画出关于轴对称的 , 点 , , 关于轴的对称点分别是 , 则点的坐标为 , 点的坐标为_______;(2)、在轴上找到一点 , 使与之和最短不写作法,保留痕迹 , 则点的坐标为______.20. 如图,是的角平分线,平分 , 交于点E.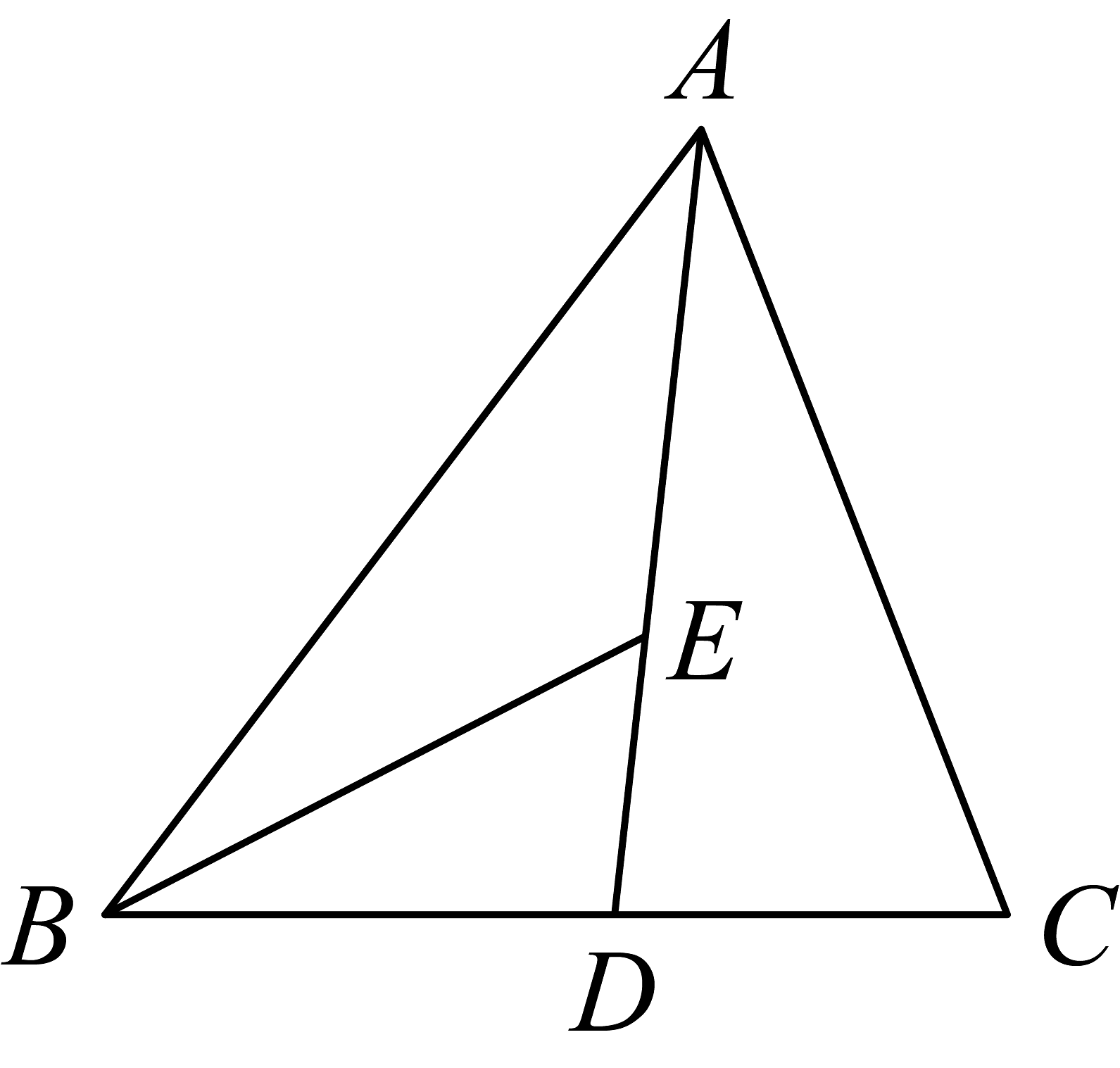 (1)、若 , 求的度数;(2)、直接写出与之间的数量关系.21. 如图,在中, , 是的平分线,于E,F在上, . 求证:
(1)、若 , 求的度数;(2)、直接写出与之间的数量关系.21. 如图,在中, , 是的平分线,于E,F在上, . 求证: (1)、;(2)、 .22. 如图
(1)、;(2)、 .22. 如图
[感知]:如图1,AD平分∠BAC,∠B+∠C=180°且∠B=90°。求证:DB=DC.
[探究]:如图2,AD平分 , 求证:.
[应用]:如图3,四边形ABDC中, , 求的值。
23. 阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,AD平分∠BAC , ∠ABC=2∠C.探究AB、BD、AC之间的数量关系;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图2,在AC上截取AE , 使得AE=AB , 连接DE , 得到全等三角形,进而解决问题.
方法二:如图3,延长AB到点E , 使得BE=BD , 连接DE , 得到等腰三角形,进而解决问题.
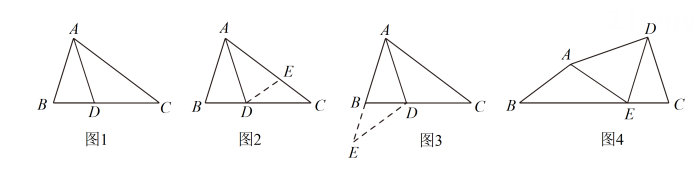 (1)、试猜想AB、BD、AC之间的数量关系 .(2)、根据阅读材料,任选一种方法证明AC=AB+BD , 根据自己的解题经验或参考小明的方法(3)、解决下面的问题;
(1)、试猜想AB、BD、AC之间的数量关系 .(2)、根据阅读材料,任选一种方法证明AC=AB+BD , 根据自己的解题经验或参考小明的方法(3)、解决下面的问题;
如图4,四边形ABCD中,E是BC上一点,EA=ED , ∠DCB=2∠B , ∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.