江苏省南京市九年级（上）数学9月份月考（范围：第一章）

试卷更新日期：2025-09-23 类型：月考试卷

进入出卷网下载

一、选择题（每题3分，共18分）

1. 一元二次方程 $2 x^{2} + x - 5 = 0$ 的二次项系数、一次项系数、常数项分别是（）

A、2，1，5 B、2，1，－5 C、2，0，－5 D、2，0，5

查看试题解析
2. 下列各数是一元二次方程 $x^{2} + 2 x - 15 = 0$ 的根的是（）

A、1 B、5 C、2 D、3

查看试题解析
3. 关于x的一元二次方程 $x^{2} + k x - 2 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 若m，n分别为一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个实数根，则 $2 m n - m - n$ 的值为（）

A、 $- 12$ B、12 C、 $- 8$ D、8

查看试题解析

二、填空题（每题3分，共30分）

5. 一元二次方程 $a x^{2} + x - 6 = 0$ 有一个根为1，则 $a =$ ．

查看试题解析
6. 已知a是方程 $x^{2} + 2 x - 2 = 0$ 的一个根，则代数式 ${(a + 1)}^{2}$ 的值为．

查看试题解析
7. 若 $x = a$ 是方程 $2 x^{2} - x - 6 = 0$ 的一个解，则代数式 $4 a^{2} - 2 a$ 的值为．

查看试题解析
8. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则实数 $m$ 的值为．

查看试题解析
9. 已知 ${(m^{2} + n^{2})}^{2} - 3 (m^{2} + n^{2}) - 10 = 0$ ，则 $m^{2} + n^{2} =$ ．

查看试题解析
10. 已知三角形的两边长分别为3和6，第三边长是方程 $x^{2} - 6 x + 8 = 0$ 的根，则这个三角形的周长为.

查看试题解析
11. 如图，某小区要在长为16m，宽为12m的矩形空地上建造一个花坛，使花坛四周小路的宽度相等，且花坛所占面积为空地面积的一半，则小路宽为m.

查看试题解析

三、解答题（共11题，共102分）

12. 解下列一元二次方程：

(1)、 x²+2x-1=0；

(2)、 2x²-x-3=0．

查看试题解析
13. 已知关于 $x$ 的一元二次方程 $x^{2} - (2 a - 1) x + a^{2} = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ．

(1)、求 $a$ 的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 6$ ，求 $a$ 的值．

查看试题解析
14. 如图，学校为美化环境，准备用总长为 $29 m$ 的篱笆，在靠墙的一侧设计一块矩形花圃 $A B C D$ ，其中墙长 $19 m$ ，花圃三边外围用篱笆围起，并在边 $B C$ 上留一个 $1 m$ 宽的门（建在 $E F$ 处，另用其他材料）．

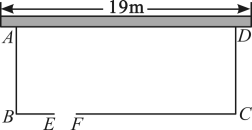(1)、若花圃的面积为 $100 m^{2}$ ，求花圃的一边 $A B$ 的长；

(2)、花圃的面积能达到 $120 m^{2}$ 吗？如果能，请你给出设计方案，如果不能，请说明理由．

查看试题解析
15. “我运动，我健康，我快乐！”随着人们对身心健康的关注度越来越高．某市参加健身运动的人数逐年增多，从2021年的32万人增加到2023年的50万人．

(1)、求该市参加健身运动人数的年均增长率；

(2)、为支持市民的健身运动，市政府决定从 $A$ 公司购买某种套装健身器材．该公司规定：若购买不超过100套，每套售价1600元；若超过100套，每增加10套，售价每套可降低40元．但最低售价不得少于1000元．已知市政府向该公司支付货款24万元，求购买的这种健身器材的套数．

查看试题解析
16. 2022北京冬奥会期间，某网店直接从工厂购进A、B两款冰墩墩钥匙扣，进货价和销售价如下表：（注：利润=销售价-进货价）
类别
价格
A款钥匙扣
B款钥匙扣
进货价（元/件）
30
25
销售价（元/件）
45
37

(1)、网店第一次用850元购进A、B两款钥匙扣共30件，求两款钥匙扣分别购进的件数；

(2)、第一次购进的冰墩墩钥匙扣售完后，该网店计划再次购进A、B两款冰墩墩钥匙扣共80件（进货价和销售价都不变），且进货总价不高于2200元．应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少？

(3)、冬奥会临近结束时，网店打算把B款钥匙扣调价销售．如果按照原价销售，平均每天可售4件．经调查发现，每降价1元，平均每天可多售2件，将销售价定为每件多少元时，才能使B款钥匙扣平均每天销售利润为90元？

查看试题解析
17. 暑假期间某景区商店推出销售纪念品活动，已知纪念品每件的进货价为30元，经市场调研发现，当该纪念品的销售单价为40元时，每天可销售280件；当销售单价每增加1元，每天的销售数量将减少10件．(销售利润=销售总额-进货成本)

(1)、若该纪念品的销售单价为45元时则当天销售量为件．

(2)、当该纪念品的销售单价为多少元时，该产品的当天销售利润是2610元．

(3)、该纪念品的当天销售利润有可能达到3700元吗?若能，请求出此时的销售单价；若不能，请说明理由．

查看试题解析
18. 用一张长为40cm，宽为25cm的长方形硬纸片，裁去一部分后折成纸盒。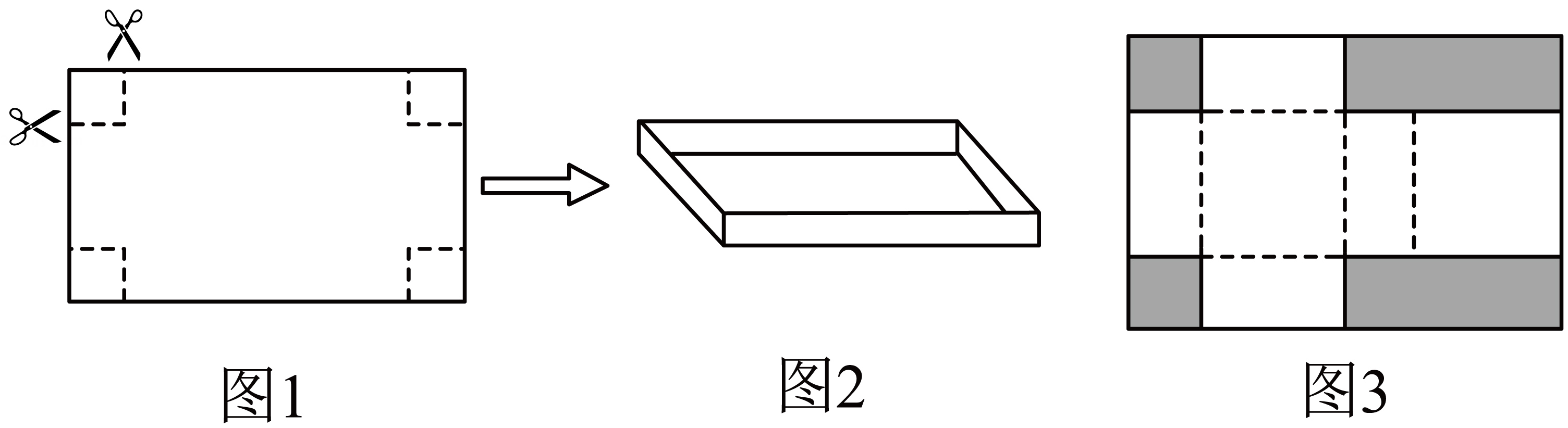

(1)、如图1裁去角上四个小正方形之后，折成如图2的无盖纸盒。若纸盒底面积为450cm² ，则纸盒的高是多少？

(2)、如图3，在纸片左边的两个角裁去两个正方形，纸片右边的两个角裁去两个长方形之后，将剩下的纸片（空白部分）折成一个有盖的纸盒。若折成纸盒的表面积为912cm² ，则裁去的正方形的边长是多少？

查看试题解析
19. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 6 c m$ ， $B C = 8 c m$ ，点P从A沿AC边向C点以1cm/s的速度移动，在C点停止，点Q从C点开始沿CB边向点B以2cm/s的速度移动，在B点停止．

(1)、如果点P ， Q分别从A、C同时出发，经过2秒钟后， $S_{△ Q P C} =$ $c m^{2}$ ；

(2)、如果点P从点A先出发2s，点Q再从点C出发，问点Q移动几秒钟后 $S_{△ Q P C} = 4 c m^{2}$ ?

(3)、如果点P、Q分别从A、C同时出发，经过几秒钟后 $P Q = B Q$ ?

查看试题解析
20. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ B = 90 °$ ， $A D = 16 cm$ ， $A B = 12 cm$ ， $B C = 21 cm$ ，动点P从点B出发，沿射线 $B C$ 的方向以每秒 $2 cm$ 的速度运动，动点Q从点A出发，在线段 $A D$ 上以每秒 $1 cm$ 的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间t（秒）．

(1)、则 $D Q =$ 　　， $P C =$ 　　（用含t的代数式表示）；

(2)、当t为何值时，以C，D，Q，P为顶点的梯形面积等于 $60 {cm}^{2}$ ？

(3)、是否存在点P，使 $△ P Q D$ 是等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

查看试题解析