-
1、如图,在△ABC中,分别延长AC , AB边上的中线BD,CE到F,G,使DF=BD,EG=CE,则下列说法:①;②;③;④四边形的面积是△ABC面积的倍,正确的个数是( )
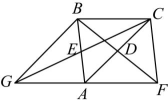 A、 B、 C、 D、
A、 B、 C、 D、 -
2、若关于x , y的方程组的解满足 , 则k的取值范围是( )A、 B、 C、 D、
-
3、《孙子算经》记载了这样一个问题“今有甲、乙二人,持钱各不知数.甲得乙中半(中半即为),可满四十八.乙得甲太半(太半即为),亦满四十八.问甲、乙二人持钱各几何?”设甲持钱x , 乙持钱y , 则根据题意可以列出方程组为( )A、 B、 C、 D、
-
4、如图, , 要说明 , 需添加的条件不能是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图,已知直线 , , 则等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、下列问题适合全面调查的是( )A、调查长沙市的自来水质量 B、调查某品牌电池的寿命 C、调查全省小学生每周的课外阅读时间 D、调查某篮球队队员的身高
-
7、在平面直角坐标系中,下列点在第四象限内的点是( )A、 B、 C、 D、
-
8、如图1,是菱形的对角线,E是上一个动点,连接 .
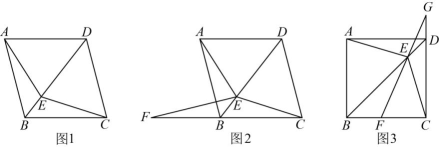 (1)、求证:;(2)、如图2,F是直线上一点,连接 , 且 .
(1)、求证:;(2)、如图2,F是直线上一点,连接 , 且 .(ⅰ)求证:;
(ⅱ)当时,如图3,延长交的延长线于点G , 探索和之间的数量关系并加以证明.
-
9、定义:若关于x的一元二次方程的两个实数根为 , , 分别以 , 为横坐标和纵坐标得到点 , 则称点M为该一元二次方程的“友好点”.已知关于x的一元二次方程为 .(1)、求证:不论m为何值,该方程总有两个不相等的实数根;(2)、求“友好点”M的坐标(用含m的式子表示);(3)、若无论为何值,关于x的方程的“友好点”M始终在直线的图象上,求b , c满足的关系.
-
10、某地2023年种植樟树港辣椒亩,由于效益不错,每年都在扩大种植面积,到今年种植了亩(1)、假定每年种植面积的年增长率相同,求种植樟树港辣椒亩数的年平均增长率;(2)、一蔬菜店以每件元的价格购进该种樟树港辣椒销售,市场调查发现,樟树港辣椒每天的销售量(件)与销售单价(元/件)之间满足一次函数关系,部分数据如下表:
销售单价(元)
销售量(件)
①求与之间的函数关系式;(不需写出自变量的取值范围).
②若要使每天的销售利润为元,又要让顾客得到实惠,销售单价应定为多少元?
-
11、学校对八年级全体学生进行了一次生物模拟测试,成绩评定分为A,B,C,D四个等级(A,B,C,D分别代表优秀、良好、合格、不合格),学校从八年级学生中随机抽取了一部分学生的成绩,绘制成以下不完整的统计图.请你根据统计图提供的信息解答下列问题;
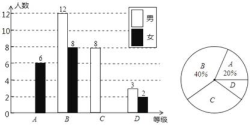 (1)、本次调查中,一共抽取了名学生的成绩;(2)、将上面的条形统计图补充完整,写出扇形统计图中等级C的百分比 .(3)、若等级D的5名学生的成绩(单位:分)分别是43、48、52、58、52.则这5个数据的中位数是分,众数是分.(4)、如果学校八年级共有500名学生,试估计在这次测试中成绩达到优秀的人数.
(1)、本次调查中,一共抽取了名学生的成绩;(2)、将上面的条形统计图补充完整,写出扇形统计图中等级C的百分比 .(3)、若等级D的5名学生的成绩(单位:分)分别是43、48、52、58、52.则这5个数据的中位数是分,众数是分.(4)、如果学校八年级共有500名学生,试估计在这次测试中成绩达到优秀的人数. -
12、已知关于的一元二次方程 .(1)、若该方程有两个实数根,求的取值范围.(2)、若该方程的两个实数根 , 满足 , 求的值.
-
13、校园规划了一片劳动基地(四边形)用来种植蔬菜和花卉.如图,花卉区和蔬菜区之间用一条长的小路隔开(小路的宽度忽略不计).经测量,花卉区的边长 , 边长 , 蔬菜区的边长 , .
 (1)、求蔬菜区边的长;(2)、求花卉区的面积.
(1)、求蔬菜区边的长;(2)、求花卉区的面积. -
14、在平面直角坐标系中,点 , .(1)、求直线的解析式;(2)、将直线向下平移4个单位后得到直线l , 求直线l 与坐标轴的交点坐标.
-
15、解下列方程:(1)、 .(2)、 .
-
16、一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为 .

-
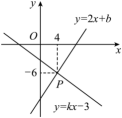
17、如图,已知一次函数和的图象交于点P , 则二元一次方程组 的解是 .
-
18、若菱形的两条对角线长分别为4和6,则该菱形的面积为 .
-
19、甲、乙、丙、丁四名学生最近5次数学测试的平均分相同,方差分别为 , , , , 则数学成绩最稳定的学生是 .
-
20、已知式子在实数范围内有意义,则x的取值范围是 .