-
1、 某校在一块矩形基地中给八年级划分出两块如图所示的农耕实践基地,中间留出一条宽度相等的人行小道,已知矩形基地的长为41m,宽为20m,农耕基地的面积为 , 若设人行小道的宽度为m,则可列方程为( )
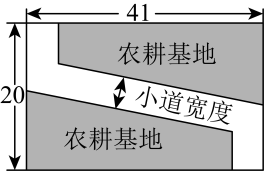 A、 B、 C、 D、
A、 B、 C、 D、 -
2、 如图,在中, , , 的平分线交于点 , 则的长为( )
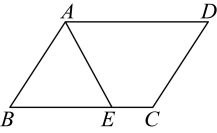 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
3、 如图,在四边形中, , , 与相邻的外角是 , 则的度数是( )
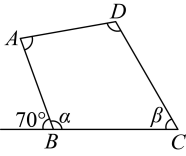 A、 B、 C、 D、
A、 B、 C、 D、 -
4、 若数据 , 3,5,的平均数为4,则数据 , 的平均数是( )A、2 B、4 C、6 D、8
-
5、 方程的解是( )A、 B、 C、 , D、 ,
-
6、 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
7、 若二次根式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、
-
8、在中, , 直线l过点C .
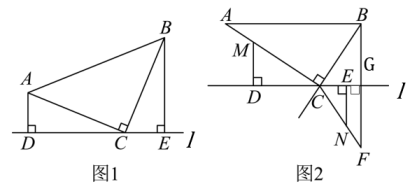 (1)、当AC=BC时,如图1,分别过点A、 B作于点D , 于点E , , , 求的长;(2)、当 , 时,如图2,BF于点G,且G为BF中点,连接BF, , 动点M从点A出发,以每秒1个单位长度的速度沿边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D , 过点N作于点E , 设运动时间为秒.
(1)、当AC=BC时,如图1,分别过点A、 B作于点D , 于点E , , , 求的长;(2)、当 , 时,如图2,BF于点G,且G为BF中点,连接BF, , 动点M从点A出发,以每秒1个单位长度的速度沿边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿向终点F运动,点M、N到达相应的终点时停止运动,过点M作于点D , 过点N作于点E , 设运动时间为秒.① ▲ ;(用含t的代数式表示)
②当N在路径上时, ▲ ;(用含的代数式表示)
③求出当与全等时的值.
-
9、在平面直角坐标系中,将点关于y轴的对称点记作点 , 再将点关于直线y=m的对称点记作点 , 则点为点关于y轴和直线y=m的“DT对称点”.例如:点P(3,1)关于y轴和直线y=3的“DT对称点”为点 .(1)、点A(3,4)关于y轴和直线y=1的“DT对称点”的坐标;(2)、点关于y轴和直线y=m的“DT对称点”的坐标是 , 求m和n的值;(3)、若点关于y轴和直线y=m的“DT对称点”在第二象限,且满足条件的x的整数解有且只有一个,求m的取值范围.
-
10、初一年级倡导书目为《我们仨》和《围城》.已知购买3本《我们仨》4本《围城》.共需160元.购进2本《我们仨》和1本《围城》.共需65元.(1)、购买一本《我们仨》和一本《围城》.各需多少钱?(2)、冰莹图书馆为方便学生借阅,计划购进两种书籍共100本,且总费用不超过2345元,预计购进《我们仨》的数量不超过《围城》数量的 , 有哪几种购买方案?
-
11、这是小明同学作一个三角形与已知三角形全等的方法:
已知:△ABC .
求作:△ABD , 使得△ABD≌ △ABC .
作法:如图.

①分别以点A , B为圆心,线段AC , BC长为半径画弧,两弧相交于点D;
②连接线段AD , BD , 则△ABD即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)、完成下面证明过程(将正确答案填在相应的横线上):证明:由作图可知,在△ABC和△ABD中,
∴△ABC≌ △ABD( ).
(2)、小甜看到小明的作图有一个特别的想法,若连接CD , 交AB于点E , 已知CD与AB的线段长能否求出△ABC的面积呢?假设CD=4,AB=6,请你尝试求出S△ABC -
12、如图,在△ABC中,AD是角平分线,BE是高,它们相交于点O
 (1)、若 , 求的度数;(2)、若∠BAD=35°,∠CBE=α,用含α的式子表示∠ADC .
(1)、若 , 求的度数;(2)、若∠BAD=35°,∠CBE=α,用含α的式子表示∠ADC . -
13、区教育局对DT中学部分学生的睡眠情况进行了问卷调查.设每名学生平均每天的睡眠时间为x小时,其中的分组情况是:
A组:x<8.5 B组:8.5≤x<9 C组:9≤x<9.5
D组:9.5≤x<10 E组:x≥10
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
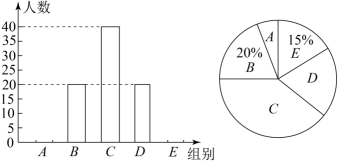 (1)、补全条形统计图;(2)、在扇形统计图中,求D组所对应的扇形圆心角的度数;(3)、DT中学现有2400名学生,请估计睡眠时间不足9小时的学生有多少人?
(1)、补全条形统计图;(2)、在扇形统计图中,求D组所对应的扇形圆心角的度数;(3)、DT中学现有2400名学生,请估计睡眠时间不足9小时的学生有多少人? -
14、如图,平面直角坐标系中,△ABC的顶点都在格点上,其中A点坐标为 .
 (1)、若把△ABC向上平移3个单位长度,再向右平移3个单位长度得到△A’B’C’ , 画出△A’B’C’;(2)、请直接写出点A’、B’、C’ 的坐标;
(1)、若把△ABC向上平移3个单位长度,再向右平移3个单位长度得到△A’B’C’ , 画出△A’B’C’;(2)、请直接写出点A’、B’、C’ 的坐标; -
15、计算:;
-
16、如图,△ABC与△BDE的顶点A、B、D在同一直线上, , , , 延长分别交、于点F、G . 若 , , 则 .
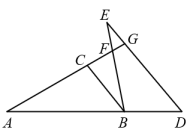
-
17、已知a , b为等腰三角形的两条边长,且a , b满足 , 则此三角形的周长为 .
-
18、不等式组的解集是 , 则 .
-
19、是方程的解,则20259a3b的值是 .
-
20、给出四个实数 , , , 0.4,其中最小的数是 .