相关试卷

1、如图，抛物线 $y = - x^{2} + m x$ 与直线 $y = x + b$ 交于点A和点B，直线 $A B$ 与y轴交于点 $C (0, - 2)$ ．

(1)、求直线和抛物线的解析式；

(2)、求点A的坐标，并结合函数图象，求出不等式 $- x^{2} + m x > x + b$ 的解集．

查看解析
2、二次函数 $y = a x^{2} + b x - 3$ 中的x，y满足下表：
x
…
$- 1$
0
1
2
3
…
$y = a x^{2} + b x - 3$
…
0
$- 3$
$- 4$
$- 3$
0
…

(1)、求此二次函数的解析式；

(2)、若 $y \geq - 3$ ，请直接写出x的取值范围．

查看解析
3、选择适当的方法解下列方程：

(1)、 $x^{2} - 7 x - 8 = 0$ ；

(2)、 $x^{2} - 2 \sqrt{3} x + 1 = 0$ ．

查看解析
4、无论x取任何实数，代数式 $\sqrt{x^{2} - k x + 3}$ 都有意义，则k的取值范围为．

查看解析
5、如果一条抛物线的形状与 $y = \frac{1}{2} x^{2} + 2$ 的形状和开口方向均相同，且顶点坐标是 $(- 4 ， 2)$ ，那么它的函数解析式为．

查看解析
6、已知二次函数 $y = - x^{2} + 2 x + 3$ ，当 $- 1 \leq x \leq 2$ 时， $y$ 的最大值与最小值之和为．

查看解析
7、抛物线 $y = (x + 5) (x - 1)$ 的对称轴为．

查看解析
8、如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于点 $(- 3, 0)$ ，其对称轴为直线 $x = - \frac{1}{2}$ ，结合图象分析下列结论：
① $a b c > 0$ ；
②对于任意实数m，都有 $\frac{1}{4} a - \frac{1}{2} b \leq a m^{2} + b n$ ；
③当 $x < 0$ 时，y随x的增大而增大；
④ $3 a + 3 b + c = 0$ ；
⑤若 $x_{1}, x_{2} (x_{1} < x_{2})$ 为方程 $a (x + 3) (x - 2) = 1$ 的两个根，则 $- 3 < x_{1} < x_{2} < 2$ ．
其中正确结论的个数有（　　）个．

A、1 B、2 C、3 D、4

查看解析
9、已知抛物线 $y = {(x - 1)}^{2} + 5$ ，平移后得到新的抛物线 $y = x^{2} + 2 x + 6$ ，则水平平移的方向和距离为（　　）

A、向左平移3个单位 B、向右平移3个单位 C、向左平移2个单位 D、向右平移2个单位

查看解析
10、已知 $A (- 1, y_{1}), B (1, y_{2}), C (4, y_{3})$ 三点都在二次函数 $y = - {(x - 3)}^{2} + k$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系为（　　）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看解析
11、若关于x的一元二次方程 $x^{2} - 6 x + 9 k = 0$ 有实数根，则k的取值范围是（　　）

A、 $k > 1$ B、 $k \geq 1$ C、 $k \leq 1$ D、 $k < 1$

查看解析
12、抛物线 $y = - 2 {(x + 1)}^{2} + 5$ 的顶点坐标为（　　）

A、 $(1, 5)$ B、 $(- 1, 5)$ C、 $(- 1, - 5)$ ） D、 $(1, - 5)$

查看解析
13、若函数 $y = (m - 1) x^{|m| + 1} + 5$ 是关于x的二次函数，则 $m =$ （　　）

A、 $- 1$ B、1 C、1或 $- 1$ D、2

查看解析
14、如图，圆O为 $Rt △ A B C$ 的外接圆， $∠ A C B = 90 ° ， B C = 4 \sqrt{3}$ ， $A C = 4$ ，点D是圆O上的动点，且点C、D分别位于 $A B$ 的两侧．

(1)、求圆O的半径；

(2)、当 $C D = 4 \sqrt{2}$ 时，求 $∠ A C D$ 的度数；

(3)、设 $A D$ 的中点为M，在点D的运动过程中，线段 $C M$ 的最大值为．

查看解析
15、如图，已知二次函数 $y = a x^{2} + 2 x + c$ 的图象与x轴交于A，B两点，A点坐标为 $(- 1, 0)$ ，与y轴交于点 $C (0, 3)$ ．

(1)、求二次函数的表达式；

(2)、在直线 $B C$ 上方的抛物线上存在点Q，使得 $∠ Q C B = 2 ∠ A B C$ ，求点Q的坐标．

查看解析
16、阅读下列材料：
解方程： $x^{4} - 6 x^{2} + 5 = 0$ ．这是一个一元四次方程，根据该方程的特点，
它的解法通常是：
设 $x^{2} = y$ ，那么 $x^{4} = y^{2}$ ，于是原方程可变为 $y^{2} - 6 y + 5 = 0$ ①，
解这个方程得： $y_{1} = 1$ ， $y_{2} = 5$ ．
当 $y_{1} = 1$ 时， $x^{2} = 1$ ． ∴ $x = \pm 1$ ；当 $y_{2} = 5$ 时， $x^{2} = 5$ ， ∴ $x = \pm \sqrt{5}$
以原方程有四个根： $x_{1} = 1$ ， $x_{2} = - 1$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$ ．
这个过程中，我们利用换元法达到降次的目的，体现了转化的数学思想．

(1)、用换元法解方程： ${(x^{2} - x)}^{2} - 4 (x^{2} - x) - 12 = 0$

(2)、 $Rt △ A B C$ 三边是 $a$ ， $b$ ， $c$ ，若两直角边 $a$ ， $b$ 满足 $(a + b) (a + b - 7) + 10 = 0$ ，斜边 $c = 4$ ，求 $Rt △ A B C$ 的面积．

查看解析
17、已知直线 $A B$ 与 $⊙ O$ 相切于点 $B$ ，连接 $O A$ 交 $⊙ O$ 于点 $C$ ．
（1）如图①，点 $D$ 是优弧 $B C$ 上一点，连接 $C D, B D$ ，若 $∠ C D B = 25 °$ ，则 $∠ B A C =$ $°$ ；
（2）如图②，延长 $A O$ 交 $⊙ O$ 于点 $D$ ，连接 $B D$ ，若 $A B = B D$ ，则 $∠ B A C =$ $°$ ；
（3）如图③，点 $E$ 是 $A O$ 上一点，且 $A E = A B$ ，连接 $B E$ 并延长交 $⊙ O$ 于点 $D$ ，连接 $O D$ ，若 $∠ B D O = 20 °$ ，则 $∠ B A C =$ $°$ ．

查看解析
18、某种麦粒在相同条件下进行发芽试验，结果如下表所示，则任取一粒麦粒，估计它能发芽的概率约为．（结果精确到 $0.01$ ）
试验的麦粒数 $n$
$100$
$200$
$500$
$1000$
$2000$
$5000$
发芽的麦粒数 $m$
$93$
$188$
$473$
$954$
$1906$
$4748$
发芽的频率 $\frac{m}{n}$
$0.93$
$0.94$
$0.946$
$0.954$
$0.953$
$0.9496$

查看解析
19、已知锐角 $△ A B C$ 中，O是 $A B$ 的中点，小明、小英二人想在 $A C$ 线段上找一点P，使得 $∠ A P B$ 为直角，其作法如图．对于小明、小英二人的作法，正确的是（）
小明的作法
过点B作与 $A C$ 垂直的直线，交 $A C$ 于点P，则P即为所求
小英的作法
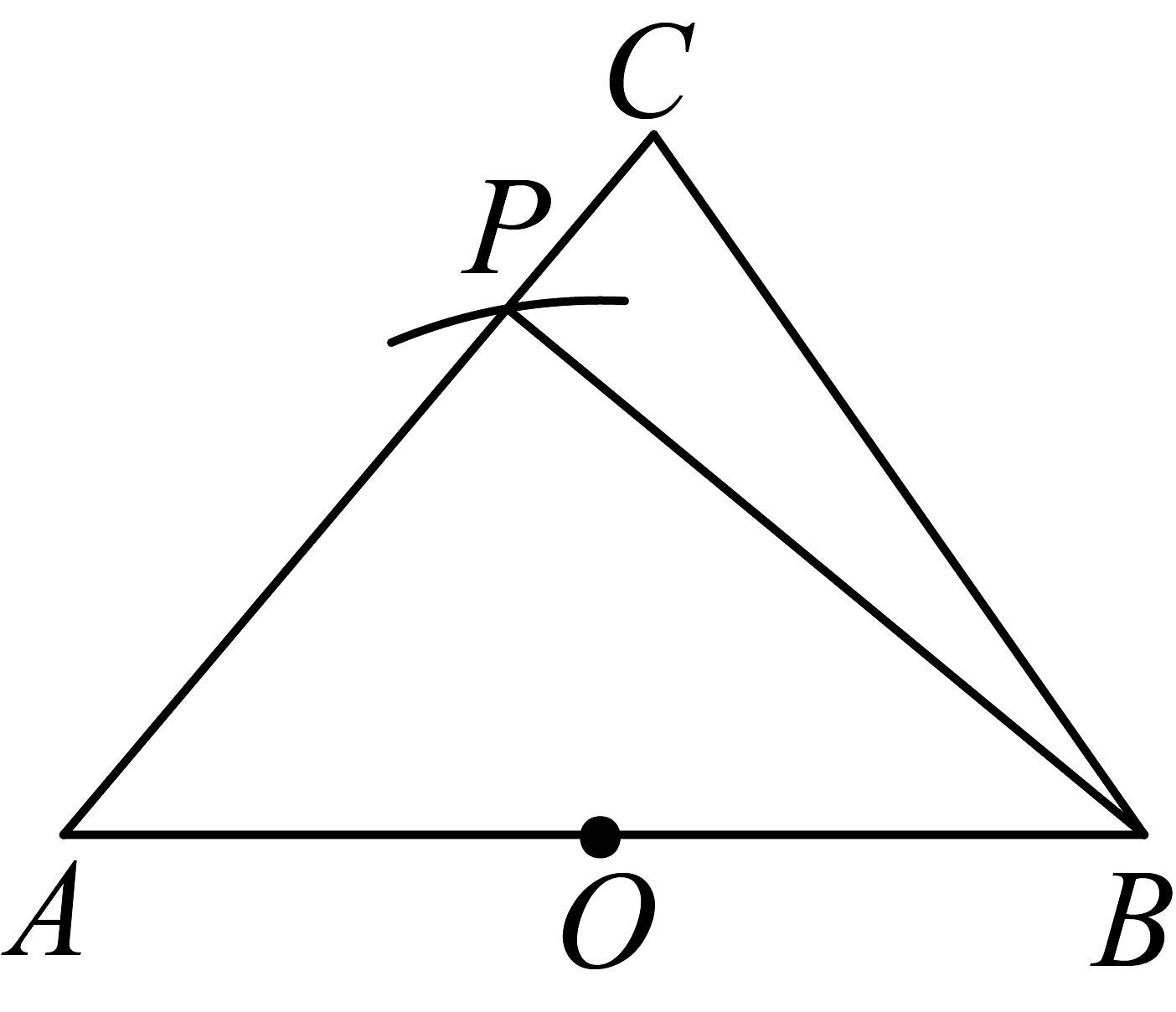
以O为圆心， $O A$ 长为半径画弧，交 $A C$ 于点P，则P即为所求

A、只有小明正确 B、只有小英正确 C、两人都正确 D、两人都不正确

查看解析
20、如图， $△ A B C$ 中， $∠ A C B = 90 ° ， A C = 3$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A^{'} B C^{'}$ ，点C的对应点 $C^{'}$ 落在 $A B$ 边上， $A^{'} B ＝ 5$ ，连接 $A A^{'}$ ．则 $A A^{'}$ 长为（　　）

A、 $2 \sqrt{2}$ B、 $\sqrt{10}$ C、3 D、4

查看解析

上一页 273 274 275 276 277 下一页跳转

x	…	$- 1$	0	1	2	3	…
$y = a x^{2} + b x - 3$	…	0	$- 3$	$- 4$	$- 3$	0	…

试验的麦粒数 $n$	$100$	$200$	$500$	$1000$	$2000$	$5000$
发芽的麦粒数 $m$	$93$	$188$	$473$	$954$	$1906$	$4748$
发芽的频率 $\frac{m}{n}$	$0.93$	$0.94$	$0.946$	$0.954$	$0.953$	$0.9496$