相关试卷
- 3.2整式的加减提升课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学六年级上学期期中仿真模拟试卷一
- 3.2 整式的加减基础课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷二(范围:1.1-4.2)
- 2.1《 事件的可能性》(2)—浙教版数学九年级上册课堂分层训练
- 浙教版数学八年级上册4.3.2 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版 数学八年级上册4.3.1 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版数学八年级上册4.2 用方向和距离确定物体的位置 同步分层练习
- 浙江省九年级上学期数学期中仿真模拟试题(一)
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
-
1、 如图,在△ABC 中,AB =4,∠BAC = 45°,∠BAC 的平分线交 BC 于点 D,E,F 分别是边AD,AB 上的动点,则 BE+EF 的最小值是.

-
2、 如图,正方形 ABCD 的对角线 AC,BD 相交于点O,点P 为 BC 边上一动点(不与点 B,C重合),PE⊥OB 于点 E,PF⊥OC 于点 F.若AB=20,则EF的最小值为 ( )
 A、10 B、 C、20 D、
A、10 B、 C、20 D、 -
3、如图,四边形ABCD是菱形,∠A=60°,延长AD 到点E,使DE=AD,连接BD,BE,CE.点P是BC的中点,M,N分别在线段CE,BE上.若AB=6,则PN+NM 的最小值为.

-
4、如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,点E是AB上任意一点,若AD=5,AC=4,则 DE 的最小值为 ( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
5、如图,抛物线 与x轴交于点A(4,0),与y轴交于点B(0,6).
 (1)、求抛物线的解析式;(2)、在x轴上有一动点 P(m,0)(点 P不与点A,点O 重合),过点 P作x轴的垂线交直线AB 于点 N,交抛物线于点 M.若 PN:MN=1:3,求m的值.
(1)、求抛物线的解析式;(2)、在x轴上有一动点 P(m,0)(点 P不与点A,点O 重合),过点 P作x轴的垂线交直线AB 于点 N,交抛物线于点 M.若 PN:MN=1:3,求m的值. -
6、如图,E是菱形ABCD对角线AC上的一点,连接BE,DE,CE=DE.
 (1)、求证:∠DEB=2∠DAB;(2)、求证:
(1)、求证:∠DEB=2∠DAB;(2)、求证: -
7、如图,在矩形 ABCD 中,点E 是 AB 的中点,点F 是 BC 上的一点,AB=8,∠FED=30°,∠FDE=45°,则 BC 的长度为.

-
8、 如图,在△ABC中,过点A 作AD⊥BC 于点D,正方形EFGH内接于△ABC,点H,G在边BC上,点 E,F分别在边AB 和AC 上.若AD=5cm,BC=10 cm,则正方形 EFGH的边长为 cm.

-
9、 如图,在⊙O 中,AB 是⊙O 的直径,CD 是⊙O 的切线,若 则⊙O的半径为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、如图,在四边形ABCD中,点 E 是BC的中点,连接AC,DE,交于点 F,且∠AFD=∠B.若CE=2,AC=5,则下列结论正确的是( )
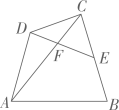 A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB
A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB -
11、 如图,在△ABC中,点 D,E分别在边AB,AC上,连接DE,且DE∥BC,若AD=3,AB=4,S四边形DECB=14,则S△ABC= ( )
 A、50 B、40 C、32 D、26
A、50 B、40 C、32 D、26 -
12、如图,在Rt△ABC中, 点D是AB边上的点, 交AC于点E, AB=10,则BC的长为.

-
13、如图,在▱ABCD中,点E 在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,DE∥BC则FD:FC的值为.
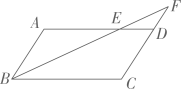
-
14、如图,四边形为正方形,且E 是边延长线上一点,过点B作 于F点, 交于H点, 交于G点, 连接 .
 (1)、求证:;(2)、求证:;(3)、求的度数.
(1)、求证:;(2)、求证:;(3)、求的度数. -
15、如图,在平面直角坐标系中,一次函数的图象与反比例函数 的图象交于点 , 与x轴交于点C.
 (1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积.
(1)、求点A 的坐标和反比例函数的解析式;(2)、根据图象直接写出不等式 的解集;(3)、点B是反比例函数图象上一点且纵坐标是1,连接 , 求 的面积. -
16、如图,四边形为菱形,点 E在的延长线上, .
 (1)、求证:;(2)、当 , 时, 求的长.
(1)、求证:;(2)、当 , 时, 求的长. -
17、在综合实践课上,数学兴趣小组用所学数学知识来解决实际问题. 实践报告如下:
实践报告
活动课题
测量河的宽度
活动工具
标杆、卷尺
测量过程
如图,为了测量河的宽度 , 小康所在的数学兴趣小组设计了如下测量方案:

【步骤一】小康站在河岸的点B处立了一根标杆; 小明站河岸的另一端点D处, 立了另一根标杆;
【步骤二】小英适当调整自己所处的位置, 在点A处测得点A, B, D恰好在同一条直线上, 点A, C, E恰好在同一条直线上;
【步骤三】其他同学用卷尺测出标杆及河岸的长;
【步骤四】记录数据 (单位:m)
标杆
1.5
标杆
1.8
河岸
10
解决问题
根据以上数据计算河的宽度.
请你帮助兴趣小组解决以上问题.
-
18、解方程∶(1)、;(2)、 .
-
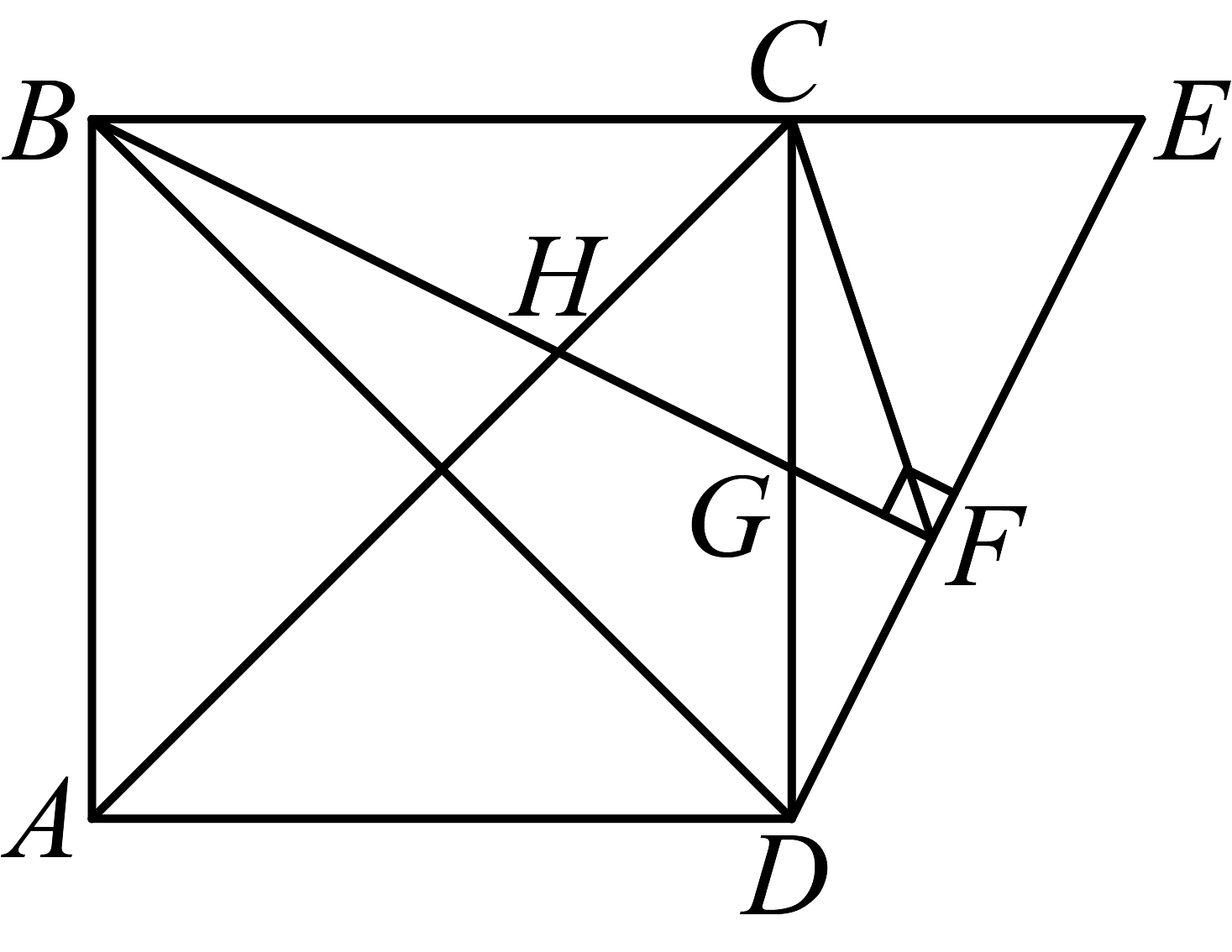
19、如图, 已知正方形的边长为30, 点E是的中点, 于H,交于G, 则 .

-
20、如图,与是位似图形, 点O为位似中心, . 若 , 则 的长是 .
