相关试卷
- 3.2整式的加减提升课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学六年级上学期期中仿真模拟试卷一
- 3.2 整式的加减基础课时卷-北师大版数学七年级上册
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷二(范围:1.1-4.2)
- 2.1《 事件的可能性》(2)—浙教版数学九年级上册课堂分层训练
- 浙教版数学八年级上册4.3.2 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版 数学八年级上册4.3.1 坐标平面内图形的轴对称和平移 同步分层练习
- 浙教版数学八年级上册4.2 用方向和距离确定物体的位置 同步分层练习
- 浙江省九年级上学期数学期中仿真模拟试题(一)
- 鲁教版(五四制)数学七年级上学期期中仿真模拟试卷一(范围:1-3章)
-
1、若aˣ=2,a3=3,则aˣ+ʸ|的值为.
-
2、下列式子运算正确的是( )A、 B、 C、 D、
-
3、计算的结果是( )A、5x2 B、5x3 C、6x2 D、6x3
-
4、下列单项式中,ab3的同类项是( )A、3ab3 B、2a2b3 C、 D、a3b
-
5、
整式的加减
同类项
所含字母相同,并且相同字母的也相同的项或几个常数项
合并
同类项法则
把同类项的系数相加,所得结果作为 , 字母和字母的指数不变
添(去)括号
对于“+”号,添(去)括号不变号;对于“一”号,添(去)括号
-
6、下列说法正确的是( )A、的系数是一2 B、32ab3的次数是6 C、是多项式 D、的常数项为1
-
7、代数式0.5中,整式的个数为( )A、3 B、4 C、5 D、6
-
8、 阅读理解
【材料阅读】赵爽在注解《周髀算经》中给出了“赵爽弦图”证明勾股定理的准确性.如图①所示,四个全等的直角三角形可以围成一个大的正方形,中间空的是一个小正方形.证明方法如下:
设直角三角形的三边中较短的直角边长为a,另一直角边长为b,斜边长为c,朱实面积=2ab,黄实面积: 朱实面积+黄实面积: 大正方形面积:

【实际应用】
若较短的直角边的长为6,另一条直角边长为8,求小正方形与大正方形的面积比;
【拓展延伸】
类比“赵爽弦图”,可构造如图②所示的图形,它是由 3个全等的三角形与中间一个小等边三角形拼成的一个大等边三角形.在△ABC中,若 求AB 的长.
-
9、勾股定理被称为几何学的基石,相传在西周由商高发现,又称商高定理,三国数学家赵爽利用弦图(它是由四个全等的直角三角形围成的),证明了商高结论的正确性.若AB=15,BC=12,将四个直角三角形中的短直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的面积(即图②阴影部分)是.

-
10、我国古代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形 ABCD,正方形 EFGH,正方形IJKL的面积分别为S1 , S2 , S3 , 若 24,则正方形 EFGH 的边长为.

-
11、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的伟大成就.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.已知大正方形的面积为25,小正方形的面积为9,设直角三角形较长直角边长为x,较短直角边长为y,下列四个说法: 25,②x-y=3,③2xy+9=25,④x+y=7.其中正确的是( )
 A、②③④ B、①②③ C、①②④ D、①②③④
A、②③④ B、①②③ C、①②④ D、①②③④ -
12、中国是发现、研究和运用勾股定理最古老的国家之一,三国时期赵爽创制了“勾股圆方图”(如图),证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD 是由4个全等的直角三角形和中间小正方形EFGH组成,连接AG.若AB=10,EF=2,则sin∠GAF 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、 某数学课外活动小组在学习了勾股定理之后,探究以四边形四条边向外作形状相同的图形的面积关系.

【问题提出】
如图①,在四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,若 求S4的值;
【拓展延伸】
如图②,在四边形ABCD中,AD∥BC,∠ABC+ , 分别以AB,AD,CD为边向四边形外作正方形,其面积分别为 求证:
-
14、 数学课上王老师和学生一起探究勾股定理和面积的拓展问题时,分别以直角三角形 ABC 的三条边为边向外作等边三角形,如图①,图中的 S1 , S2 , S3满足的数量关系是;如图②,将△ABF 沿着 AB 翻折得到△ABF',若 , 则△ABC 的面积是.

-
15、如图,以AC 为直径画半圆,在半圆上取一点 B,连接AB,BC,分别以AB,BC为直径画半圆,则图中阴影部分的面积与△ABC的面积关系为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
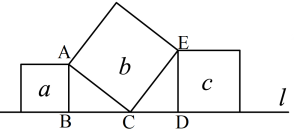
16、 如图,直线l上有三个正方形a,b,c,若b,c的面积分别为8和5,则a的面积为( )
A、2 B、 C、3 D、4 -
17、如图,分别以 的三边为斜边向外作等腰直角三角形,若图中阴影部分的面积为100,则AF的长为 ( )
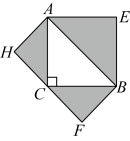 A、10 B、 C、20 D、
A、10 B、 C、20 D、 -
18、(1)、问题提出
如图①,△ABC是边长为2 的等边三角形,点 E 为 BC 边上一动点,连接AE,求AE的最小值;
 (2)、问题解决
(2)、问题解决如图②,某小区现有一片菱形空地AB-CD,其中AB=60 m,∠B=60°,为了美化环境,该小区计划在这块空地里种植两种花卉,并修建三条小道AE,AF,EF 供居民观赏,根据设计要求:点 E,F 分别在 BC,CD边上,且∠EAF=60°.现计划在△AEF 内种植玫瑰,其余空地种植郁金香,试求按设计要求,玫瑰的种植面积最小为多少?

-
19、如图,抛物线 与x轴交于A,B 两点(点A 在点 B 左侧),与y轴交于点 C,P 是直线 BC 上一动点,Q是x轴上一动点,连接AP,PQ,则AP+PQ的最小值为.

-
20、如图,在等腰三角形ABC中,点 D 为AC的中点,M,N分别是AB,BC 上的动点,若CD=2,∠A=120°,则 DN+MN 的最小值为.
