-
1、观察算式 , 在解题过程中,能使运算变得简便的运算律是( )A、乘法交换律 B、乘法结合律 C、分配律 D、乘法交换律和乘法结合律
-
2、在下列数中:0, , , , 3.14, , 0.3131131113…(每两个3之间依次多一个1),有理数有( )A、3个 B、4个 C、5个 D、6个
-
3、数轴上点与点之间的距离记为: . 如图,在数轴上 , , 三点对应的数分别为 , , , 已知 , , 且点 , 点到点的距离相等,即 .
 (1)、填空:点对应的数为 ;(2)、若点从点出发,以个单位/秒的速度沿数轴向右移动,同时点从点出发,以个单位/秒的速度向右移动,在点 , 移动的同时点从点出发,以个单位/秒的速度沿数轴向右移动,设移动时间为秒.
(1)、填空:点对应的数为 ;(2)、若点从点出发,以个单位/秒的速度沿数轴向右移动,同时点从点出发,以个单位/秒的速度向右移动,在点 , 移动的同时点从点出发,以个单位/秒的速度沿数轴向右移动,设移动时间为秒.①若点到的距离是点到的距离的两倍,我们就称点是的“幸福点”.当点是的“幸福点”时,求此时点对应的数;
②在三个点移动的过程中,或在某种条件下是否会为定值,请分析并说明理由.
-
4、已知 .(1)、求;(2)、求;(3)、如果 , 那么C的表达式是什么?
-
5、底面积为 , 高为的圆柱形容器内有若干水,水位高度为 , 现将一个边长为的立方体铁块水平放入容器底部,立方体完全沉没入水中(如图甲).再将一个边长为的立方体铁块水平放在第一个立方体上面,若第二个立方体只有一半没入水中(如图乙).此时水位高度为 , 若 , 则 .

-
6、若是方程的解,则代数式的值为 .
-
7、多项式的一次项是 .
-
8、比较大小:0 , , . (填“”,“”号)
-
9、若用表示任意正实数的整数部分,例如: , , , 则式子的值为( )(式子中的“”,“”依次相间)A、22 B、 C、23 D、
-
10、如图, 数轴上两点分别对应实数 , 则化简的结果是( )
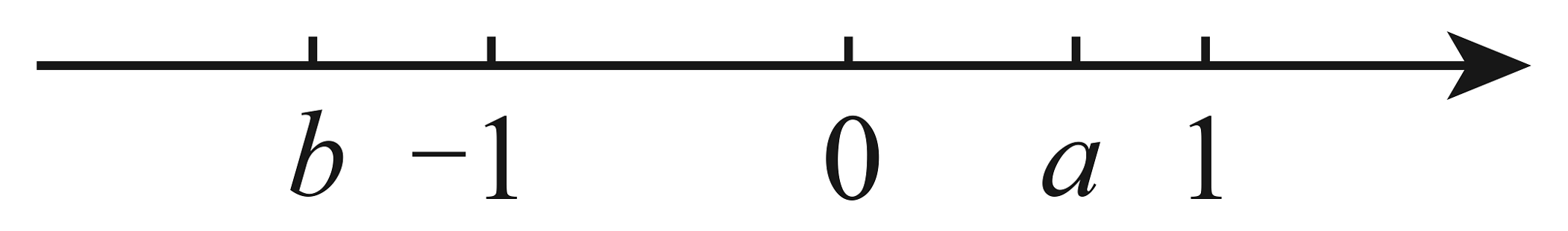 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .
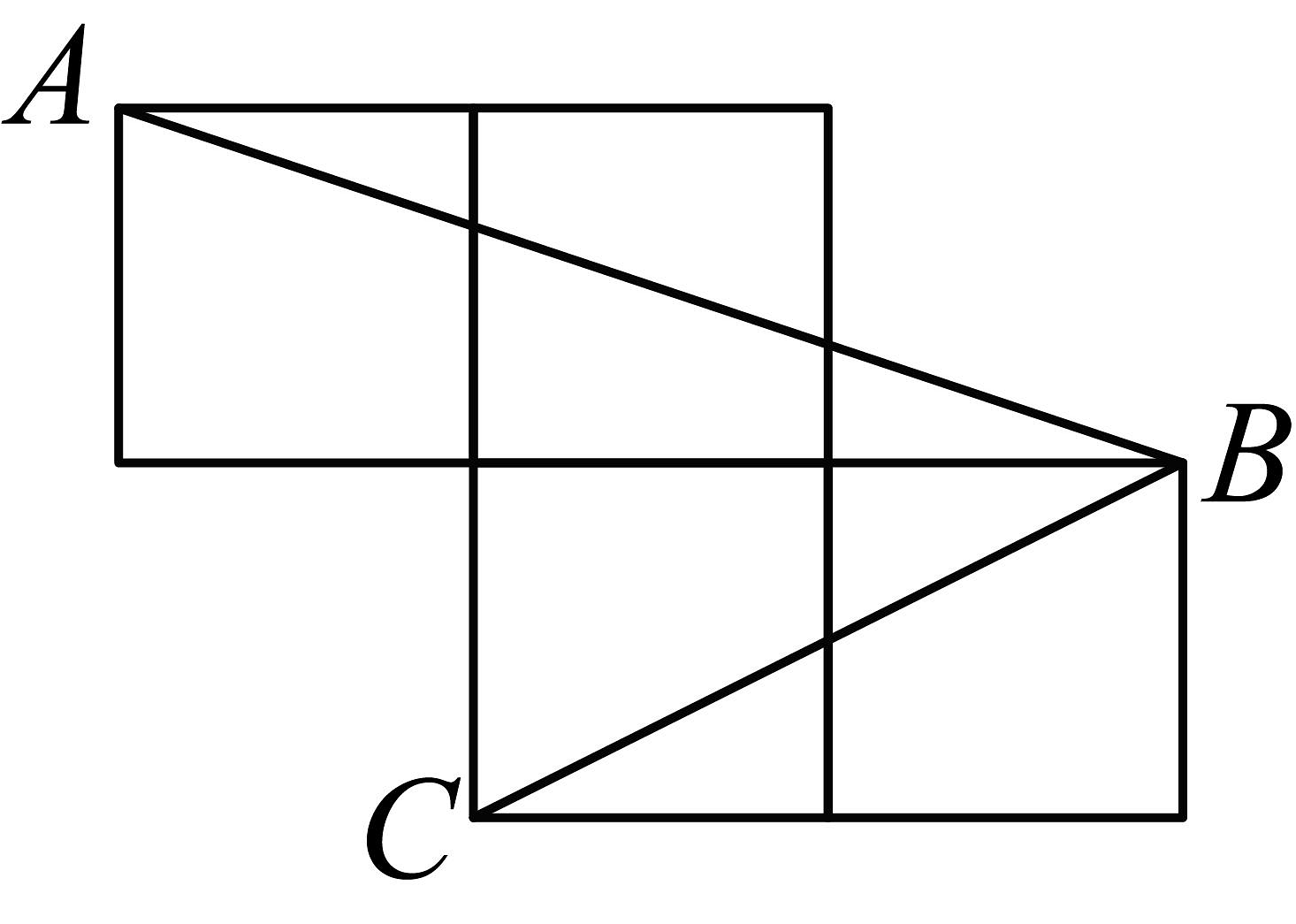
-
12、如图①,在中, , , , 将沿方向平移 , 得到 , 过点作 , 交的延长线于点 , 为的中点.点从点出发,沿方向匀速运动,速度为;同时,点从点出发,沿方向匀速运动,速度为 . 连接 , , . 设运动时间为() .
解答下列问题:
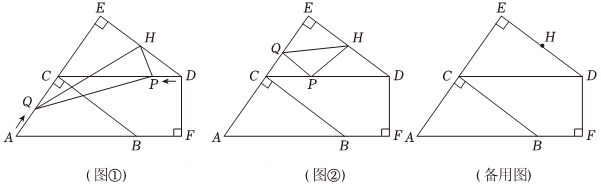 (1)、当时,求的值;(2)、如图②,当时,设的面积为(),求与之间的函数关系式;(3)、当时,是否存在某一时刻 , 使是直角三角形?若存在,求出的值;若不存在,请说明理由.
(1)、当时,求的值;(2)、如图②,当时,设的面积为(),求与之间的函数关系式;(3)、当时,是否存在某一时刻 , 使是直角三角形?若存在,求出的值;若不存在,请说明理由. -
13、小磊和小明练习打网球.在一次击球过程中,小磊从点正上方1.8米的点将球击出.
信息一:在如图所示的平面直角坐标系中,为原点,在轴上,球的运动路线可以看作是二次函数( , 为常数)图象的一部分,其中(米)是球的高度,(米)是球和原点的水平距离,图象经过点 , .
信息二:球和原点的水平距离(米)与时间(秒)()之间近似满足一次函数关系,部分数据如下:
(秒)
0
0.4
0.6
…
(米)
0
4
6
…
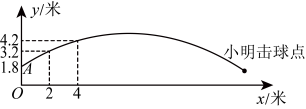 (1)、求与的函数关系式;(2)、网球被击出后经过多长时间达到最大高度?最大高度是多少?(3)、当为秒时,小明将球击回、球在第一象限的运动路线可以看作是二次函数( , 为常数)图象的一部分,其中(米)是球的高度,(米)是球和原点的水平距离.当网球所在点的横坐标为 , 纵坐标大于等于时,的取值范围为(直接写出结果).
(1)、求与的函数关系式;(2)、网球被击出后经过多长时间达到最大高度?最大高度是多少?(3)、当为秒时,小明将球击回、球在第一象限的运动路线可以看作是二次函数( , 为常数)图象的一部分,其中(米)是球的高度,(米)是球和原点的水平距离.当网球所在点的横坐标为 , 纵坐标大于等于时,的取值范围为(直接写出结果). -
14、【定义新运算】
对正实数 , , 定义运算“”,满足 .
例如:当时, .
(1)、当时,请计算:;【探究运算律】
对正实数 , , 运算“”是否满足交换律?
,
,
.
运算“”满足交换律 .
(2)、对正实数 , , , 运算“”是否满足结合律?请说明理由;(3)、【应用新运算】如图,正方形是由四个全等的直角三角形和中间的小正方形拼成, , , 且 . 若正方形与正方形的面积分别为26和16,则的值为 .
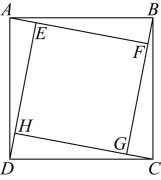
-
15、如图,在中,为的中点,为延长线上一点,连接 , , 过点作交的延长线于点 , 连接 .
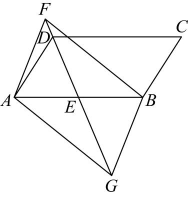 (1)、求证:;(2)、已知 ▲ (从以下两个条件中选择一个作为已知,填写序号),请判断四边形的形状,并证明你的结论.
(1)、求证:;(2)、已知 ▲ (从以下两个条件中选择一个作为已知,填写序号),请判断四边形的形状,并证明你的结论.条件①:;
条件②: .
-
16、某公司成功研发了一款新型产品,接到了首批订单,产品数量为2100件.公司有甲、乙两个生产车间,甲车间每天生产的数量是乙车间的1.5倍.先由甲、乙两个车间共同完成1500件,剩余产品再由乙车间单独完成,前后共用10天完成这批订单.(1)、求甲、乙两个车间每天分别能生产多少件产品;(2)、首批订单完成后,公司将继续生产30天该产品,每天只能安排一个车间生产,如果安排甲车间生产的天数不多于乙车间的2倍,要使这30天的生产总量最大,那么应如何安排甲、乙两个车间的生产天数?
-
17、学校综合实践小组测量博学楼的高度.如图,点 , , , , 在同一平面内,点 , , 在同一水平线上,一组成员从19米高的厚德楼顶部测得博学楼的顶部的俯角为 , 另一组成员沿方向从厚德楼底部点向博学楼走15米到达点,在点测得博学楼顶部的仰角为 , 求博学楼的高度.(参考数据: , , , , , )
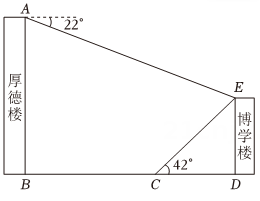
-
18、某校举行科技节,科技小组为了解学生使用智能软件的情况开展了统计活动.
【收集数据】
科技小组设计了如下调查问卷,在全校随机抽取部分学生进行调查,收集得到“问题1”和“问题2”的数据.(被调查学生两个问题全部按要求作答并提交)
调查问卷
问题1:你使用智能软件的主要目的是( ).(单选)
A.学习管理
B.健康
C.时间管理
D.其他
问题2:你每周使用智能软件的时间是____分钟.
【整理和表示数据】
第一步:将“问题1”的数据进行整理后,绘制成如下的人数统计表;
第二步:将“问题2”中每周使用智能软件的时间(分钟)整理分成4组:① , ② , ③ , ④ , 并绘制成如下的频数直方图.
学生使用智能软件主要目的的人数统计表
目的
人数累计
人数
A
正正正正正正
30
B
正正丅
12
C
正正正
15
D
3
学生每周使用智能软件时间的频数直方图
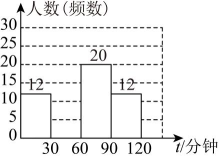 (1)、若将“问题1”的数据绘制成扇形统计图,则目的“B”对应的扇形圆心角的度数为°;(2)、补全频数直方图;(3)、【分析数据,解答问题】
(1)、若将“问题1”的数据绘制成扇形统计图,则目的“B”对应的扇形圆心角的度数为°;(2)、补全频数直方图;(3)、【分析数据,解答问题】已知“”这组的数据是:60,60,62,62,63,65,65,65,70,70,75,75,75,75,75,80,80,80,80,85.被调查的全部学生每周使用智能软件时间的中位数为分钟;
(4)、全校共有1200名学生,请你估计使用智能软件主要用于“学习管理”的人数. -
19、京剧以其独特的艺术魅力和深厚的文化底蕴闻名于世,京剧的角色有生、旦、净、丑等.现有4张不透明卡片,正面分别印有“生”、“旦”、“净”、“丑”四种角色的卡通人物,卡片除正面图案外其余都相同.将这4张卡片背面朝上洗匀,先随机抽取一张,再从剩下的3张中随机抽取一张.利用画树状图或列表的方法表示所有可能出现的结果,并求抽取到的两张卡片中有“生”的概率.
-
20、(1)、计算:;(2)、解不等式组:并写出它的整数解.