相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、如图,在△ABC 中,AB=AC,∠A=30°,射线CP 从射线 CA 开始绕点C逆时针旋转角 与射线AB相交于点 D,将△ACD 沿射线 CP 翻折至△A'CD 处,射线 CA'与射线 AB 相交于点E.若△A'DE 是等腰三角形,则∠α的度数为

-
2、 综合与实践
某次“综合与实践”活动课的主题为:研究矩形背景下的一类折叠问题,折痕为过矩形的其中一个顶点,在矩形 ABCD 中,AB = AD,E是AD 上一点(不与点 D重合),将△CDE沿CE 折叠,点 D 的对应点D'落在矩形内或矩形的边上.
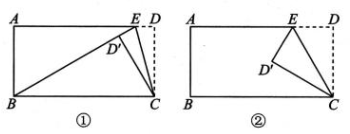 (1)、【特殊位置研究】
(1)、【特殊位置研究】如图①,若点 D'恰好落在线段 BE上,试求∠DCE 的度数;
(2)、【一般路径探索】如图②,已知AB=4,连结AD',试求 AD'的最小值;
(3)、【图形拓展深化】在(2)的条件下,连结 AD', BD',若△ABD'是等腰三角形,试求 DE 的长.
-
3、 如图,▱ABCD 的对角线AC,BD 相交于点O,AB⊥AC,AB=3,∠ACB=30°,点P 从点A 出发,沿AD以1个单位/秒的速度向终点 D 运动,连结 PO并延长交 BC 于点Q.设点 P 的运动时间为t秒.
 (1)、BQ=(用含t的代数式表示);当t=时,四边形 ABQP 是平行四边形.(2)、在点 P 的运动过程中,当t为何值时,△APO是直角三角形?(3)、在点 P 的运动过程中,当t 为何值时,△APO是等腰三角形?
(1)、BQ=(用含t的代数式表示);当t=时,四边形 ABQP 是平行四边形.(2)、在点 P 的运动过程中,当t为何值时,△APO是直角三角形?(3)、在点 P 的运动过程中,当t 为何值时,△APO是等腰三角形? -
4、综合与实践
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验,让我们一起动手来折一折、转一转,体会活动带给我们的乐趣.
折一折:将正方形纸片 ABCD 折叠,使边AB,AD 都落在对角线AC 上,展开得折痕AE,AF,连结EF,如图①.
 (1)、∠EAF=°,写出图中两个等腰三角形:(不添加辅助线和字母);转一转:将图①中的∠EAF 绕点 A 旋转,使它的两边分别交边 BC,CD 于点 P,Q,连结PQ,如图②.(2)、线段 BP,PQ,DQ 之间的数量关系为;(3)、连结正方形 ABCD 的对角线 BD,若图②中的∠PAQ的边AP,AQ分别交对角线BD于点M,N,如图③,求 的值.
(1)、∠EAF=°,写出图中两个等腰三角形:(不添加辅助线和字母);转一转:将图①中的∠EAF 绕点 A 旋转,使它的两边分别交边 BC,CD 于点 P,Q,连结PQ,如图②.(2)、线段 BP,PQ,DQ 之间的数量关系为;(3)、连结正方形 ABCD 的对角线 BD,若图②中的∠PAQ的边AP,AQ分别交对角线BD于点M,N,如图③,求 的值. -
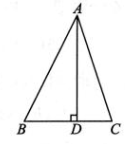
5、 如图,在△ABC 中,∠BAC=45°,AD⊥BC,垂足为 D.若BD=6,CD=4,求高线AD的长.
-
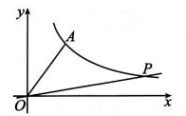
6、如图,已知反比例函数 的图象经过点A(3,4),在该图象上找一点 P,使∠POA=45°,则点 P 的坐标为 .
-
7、如图,在平面直角坐标系中,一次函数 y =2x-2 的图象分别交x轴、y轴于点A,B,直线 BC与x 轴正半轴交于点C.若∠ABC=45°,则直线 BC的函数表达式是( )
 A、y=3x-2 B、 C、 D、
A、y=3x-2 B、 C、 D、 -
8、 如图,在矩形ABCD 中,AB=14,E 是BC边上一点,且 BE=6,连结 AE,AC.若∠CAE=45°,则CE的长为 ( )
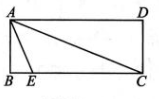 A、20 B、29 C、 D、
A、20 B、29 C、 D、 -
9、题目:“如图 ,∠B=45°,BC=2,在射线 BM上取一点A,设AC=d,若对于d的一个数值,只能作出唯一一个△ABC,求d的取值范围.”对于其答案,甲答:d≥2,乙答:d=1.6,丙答: 则正确的是( )
 A、只有甲答得对 B、甲、丙的答案合在一起才完整 C、甲、乙的答案合在一起才完整 D、三人的答案合在一起才完整
A、只有甲答得对 B、甲、丙的答案合在一起才完整 C、甲、乙的答案合在一起才完整 D、三人的答案合在一起才完整 -
10、如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D 是AC上一点,CE⊥BD交直线 BD 于点E,且∠AEB=45°.若BE=7,AE=3 , F为BC的中点,连结EF,则EF的长为 ( )
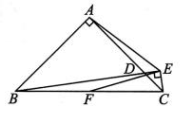 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,在△ABC中,分别过点 B,A 作 BD⊥AC于点 D,AE⊥BC于点 E,BD,AE交于点 F.若∠BAC=45°,AD=5,CD=2,则线段 BF的长度为 ( )
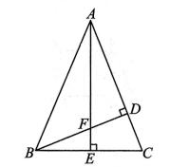 A、2 B、 C、3 D、
A、2 B、 C、3 D、 -
12、
 (1)、如图①,已知 OC 是∠AOB 的平分线,P是OC上任意一点,点D,E分别在边 OA,OB 上,连 结 PD,PE,∠AOB +∠DPE=180°.若∠AOB=60°,OD+OE= , 则OP的长为;(2)、如图②,在▱ABCD 中,∠ABC=60°,BE平分∠ABC交AD 于点E,连结CE,将CE 绕点 E 旋转,当点 C 的对应点 F 落在边AB 上时,若 求四边形BCEF的面积.
(1)、如图①,已知 OC 是∠AOB 的平分线,P是OC上任意一点,点D,E分别在边 OA,OB 上,连 结 PD,PE,∠AOB +∠DPE=180°.若∠AOB=60°,OD+OE= , 则OP的长为;(2)、如图②,在▱ABCD 中,∠ABC=60°,BE平分∠ABC交AD 于点E,连结CE,将CE 绕点 E 旋转,当点 C 的对应点 F 落在边AB 上时,若 求四边形BCEF的面积. -
13、 在△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点 D.
 (1)、如图①,F 为 BC 上一点,连结 AF交BD于点E.若AB=BF,求证:BD垂直平分AF;(2)、如图②,CE⊥BD,垂足 E 在 BD 的延长线上,试判断线段CE,BD 之间的数量关系,并说明理由;(3)、如图③,F 为 BC 上一点,∠EFC= ∠ABC,CE⊥EF,垂足为E,EF与AC 交于点M.直接写出线段CE,FM之间的数量关系.
(1)、如图①,F 为 BC 上一点,连结 AF交BD于点E.若AB=BF,求证:BD垂直平分AF;(2)、如图②,CE⊥BD,垂足 E 在 BD 的延长线上,试判断线段CE,BD 之间的数量关系,并说明理由;(3)、如图③,F 为 BC 上一点,∠EFC= ∠ABC,CE⊥EF,垂足为E,EF与AC 交于点M.直接写出线段CE,FM之间的数量关系. -
14、 如图,四边形 ABCD为平行四边形,∠BAD的平分线AF交CD 于点E,交 BC的延长线于点 F,连结 BE.若 BE⊥AF,EF= , 则AB的长为.

-
15、如图,AE,BE,CE分别平分∠BAC,∠ABC,∠ACB,ED⊥BC于点D,ED=3,△ABC的面积为 36,则△ABC的周长为 ( )
 A、48 B、36 C、24 D、12
A、48 B、36 C、24 D、12 -
16、如图,在△ABC中,AD平分∠BAC,E 是BC的中点,BD⊥AD 于点D.若AC=7,AB=4,则DE的长为 ( )
 A、1 B、2 C、 D、
A、1 B、2 C、 D、 -
17、 【阅读材料】
问题
如图,AB,CD 相交于点O,O 是 AB 的中点,AC∥BD,求证:O是CD 的中点.

问题分析
由条件易证△AOC≌△BOD,从而得到OC=OD,即O是CD 的中点.
方法提取
构造“平行8字形”全等三角形模型是证明线段相等的一种常用方法.
请运用上述阅读材料中获取的经验和方法解决下列问题.
【基础应用】
已知在△ABC中,. 点 E 在边 AB 上,点F 在边 BC的延长线上,连结EF交AC 于点 D.
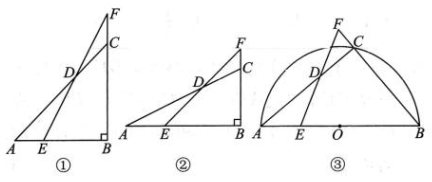 (1)、如图①,若AB=BC,AE=CF,求证:D是EF的中点;(2)、如图②,若AB=2BC,AE=2CF,探究CD 与 BE 之间的数量关系;(3)、【灵活应用】
(1)、如图①,若AB=BC,AE=CF,求证:D是EF的中点;(2)、如图②,若AB=2BC,AE=2CF,探究CD 与 BE 之间的数量关系;(3)、【灵活应用】如图③,AB是半圆O的直径,C是半圆上一点,E 是AB 上一点,点 F 在 BC 的延长线上, 当点C从点B运动到点A,点D运动的路径长为 , CF 扫过的面积为.
-
18、【问题呈现】小明在数学兴趣小组活动时遇到一个几何问题:如图①,在等边三角形ABC中,AB=3,点M,N分别在边 AC,BC上,且 AM=CN,试探究线段MN长度的最小值.
【问题分析】小明通过构造平行四边形,将双动点问题转化为单动点问题,再通过定角发现这个动点的运动路径,进而解决上述几何问题.
【问题解决】如图②,过点C,M分别作MN,BC的平行线,并交于点 P,作射线 AP.

在【问题呈现】的条件下,回答下列问题:
(1)、求证:AM=MP;(2)、∠CAP 的大小为度,线段 MN长度的最小值为.(3)、【方法应用】某种简易房屋在整体运输前需用钢丝绳进行加固处理,如图③.小明收集了该房屋的相关数据,并画出了示意图,如图④,△ABC是等腰三角形,四边形 BCDE 是矩形,AB=AC=CD=2米,∠ACB=30°.MN是一条两端点位置和长度均可调节的钢丝绳,点 M在AC 上,点 N 在 DE 上.在调整钢丝绳端点位置时,其长度也随之改变,但需始终保持AM=DN.钢丝绳 MN长度的最小值为米. -
19、小明在求代数式 的最小值时,采用如下方法:如图,在平面直角坐标系中,设M(x,0)为x轴上的一个动点,选取点 A(0,1)和B(4,2),根据两点之间的距离公式,得 通过构造,将求代数式的最小值转化为求AM+BM的最小值.由此小明求出 的最小值为.

-
20、如图,在 Rt△ABC 中,∠ACB=90°,AB=2,若 D 为直线 AC左侧一点,当△ABC∽△CAD时,BC+CD的最大值为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、