广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期：2018-03-06 类型：期末考试
一、选择题
-
1. 下列大学的校徽图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 要使分式 有意义，则x的取值范围是（ ）A、x≠1 B、x>1 C、x<1 D、x≠-13. 以下各组线段为边，能组成三角形的是（ ）A、2cm，4cm，6cm B、8cm，6cm，4cm C、14cm，6cm，7cm D、2cm，3cm，6cm4. 计算x2y2(-xy3)2的结果是（ ）
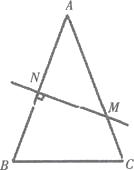
A、x5y10 B、x4y8 C、-x5y8 D、x6y125. 如图，AB=BD，AC=CD，则全等三角形共有（ ）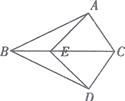
A、1对 B、2对 C、3对 D、4对6. 下列计算中正确的是（ ）A、a2+b3_-2a5 B、a4·a=a4 C、a2·a4=a8 D、(-a2)3=-a67. 一个三角形的两边长分别为3cm和7cm，则此三角形第三边长可能是（ ）A、3cm B、4 cm C、7 cm D、11cm8. 因式分解：2a(x-y)+3b(y-x)正确的是（ ）
A、(x-y)(2a-3b) B、(x+y)(2a-3b) C、(y-x)(2a+3b) D、(x+y)(2a+3b)9. 下列计算中，正确的个数有（ ）①3x3·(-2x2)=-6x5 ②4a3b÷(-2a2b)=-2a
③(a3)2=a5 ④(-a)3÷(-a)=-a2
A、1个 B、2个 C、3个 D、4个10. 施工队要铺设一段长2000米的管道，因在中考期间需要停两天，实际每天施工需要比计划多50米，才能按时完成任务．求原计划每天施工多少米．设原计划每天施工x米．则根据题意所列方程正确的是（ ）
A、 - =2 B、 - =2 C、 - =2 D、 - =2二、填空题
-
11. 化简： = ．
12. 若点A(3，-2)与点B关于Y轴对称，则点B的坐标为 ．
13. 若x2+mx+9是一个完全平方式，则m的值是 ．
14. 一个四边形，截一刀后得到的新多边形的内角和最多为 ．15. 若3x=15，3y=5，则3x-y= ．
16. 将一副直角三角板如下图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．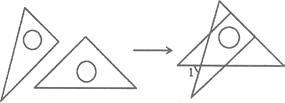
三、解答题
-
17. 化简：
18. 先将分式(1+ )÷ 进行化简，然后请你给x选择一个合适的值，求原式的值．
19. 某班举行文艺晚会，桌子摆成两直条(如图中的AO，BO)，AO桌面上摆满了桔子。BO桌面上摆满了糖果，坐在C处的学生小明先拿桔子再拿糖果，然后回到空座位D上．请你帮助他设计一条行走路线，使其所走的总路程最短?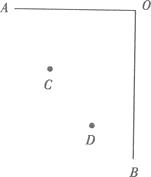
四、解答题
-
20. 解分式方程： +1=21. 张老师和李老师住在同一个小区，离学校3000米，某天早晨，张老师和李老师分别于7点10分、7点15分离家骑自行车上班，刚好在校门口遇上，已知李老师骑车的速度是张老师的1.2倍，求他们各自骑自行车的速度分别是多少米/分?
22. 如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．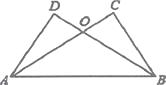
求证：
(1)、BC=AD；
(2)、△OAB是等腰三角形．
五、解答题
-
23. 在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF
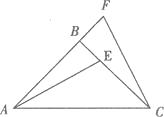(1)、求证：Rt△ABE≌Rt△CBF；(2)、若∠CAE=30。 ， 求∠ACF的度数．
