相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、2024年东港市某中学要建一长方形停车场,其中一面靠墙,其他三面用护栏围起,已知长方形停车场的长为米,宽比长少米.
 (1)、用 , 表示长方形停车场的宽.(2)、求护栏的总长度.(3)、若 , , 每米护栏造价70元,求建此停车场所需的费用.
(1)、用 , 表示长方形停车场的宽.(2)、求护栏的总长度.(3)、若 , , 每米护栏造价70元,求建此停车场所需的费用. -
2、如图是一组有规律的图案,它们是由边长相同的小正方形组成的,其中部分小正方形涂有阴影,依此规律,第个图案中有个阴影小正方形(用含有的代数式表示).

-
3、甲、乙两个足球队连续打对抗赛,规定胜一场得分,平一场得分,负一场得分,共赛场,甲队保持不败,得分,甲队胜场.
-
4、下列四个几何体中,是圆柱的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、如图,数轴上被墨水遮盖的数可能为( )
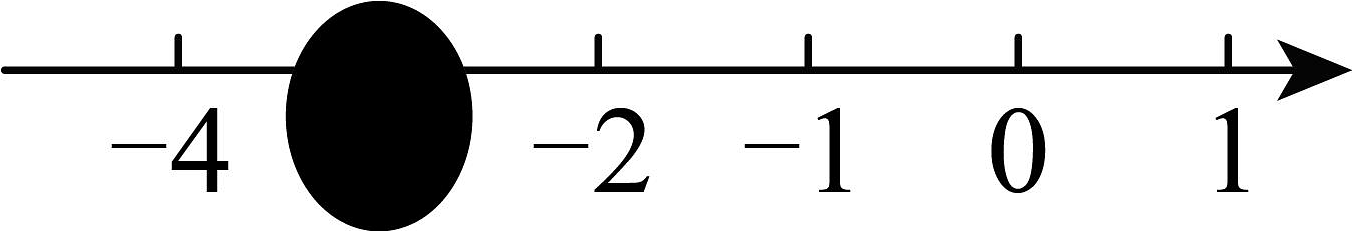 A、 B、 C、 D、
A、 B、 C、 D、 -
6、下列图形中,属于立体图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
7、比-3℃低7℃的温度是( )A、4℃ B、-4℃ C、10℃ D、=10℃
-
8、用代数式表示“m的3倍与n的差的平方”,正确的是( )A、 B、 C、 D、
-
9、如图,为的直径,过圆上一点D作的切线交的延长线于点C,过点O作交于点E,连接 .
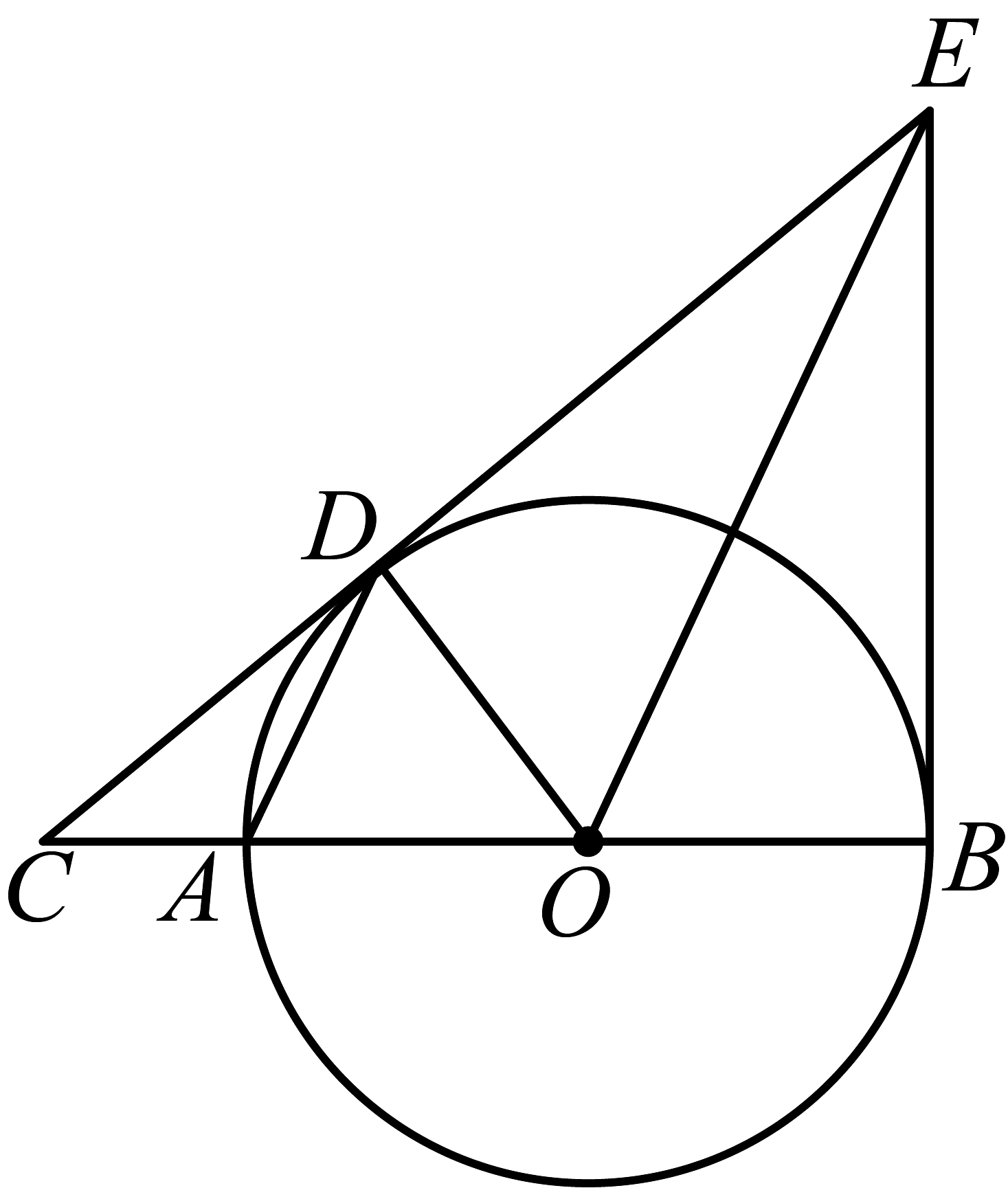 (1)、求证:直线是的切线;(2)、若 , , 求的半径及的长.
(1)、求证:直线是的切线;(2)、若 , , 求的半径及的长. -
10、解下列方程:(1)、(2)、
-
11、若抛物线向左平移1个单位长度,向下平移2个单位长度,则所得的抛物线的解析式是 .
-
12、如图,将绕点逆时针旋转得到 , 若点在线段的延长线上, , 则旋转角的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,一个底部呈球形的烧瓶,球的半径 , 瓶内液体的最大深度 , 则截面圆中弦的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图所示,A是上一点,且 , , , 则与的位置关系是( )
 A、相离 B、相切 C、相交 D、相割
A、相离 B、相切 C、相交 D、相割 -
15、对于二次函数的图象,下列说法正确的是( )A、开口向上 B、对称轴是直线 C、当时,y随x的增大而增大 D、顶点坐标为
-
16、已知抛物线的顶点为D,与轴交于A,B两点(A在B左边),与y轴交于点C
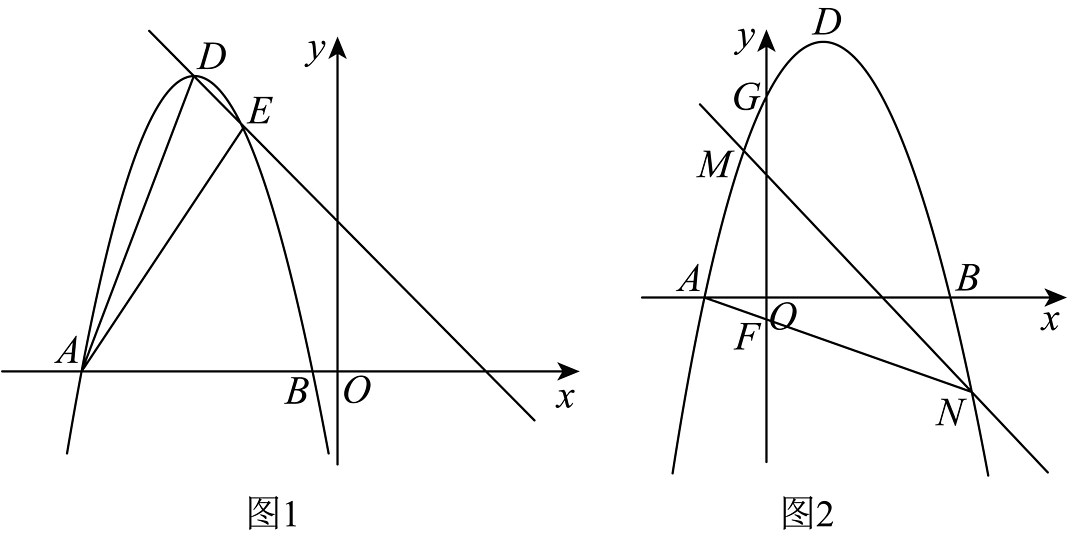 (1)、若点A坐标为 , 点C坐标为求其解析式;(2)、如图(1),已知抛物线的顶点D在直线:上滑动,且与直线交于另一点E,若的面积为 , 求此时点A的坐标;(3)、如图(2),在(1)的条件下,直线交抛物线于M,N两个不同的点,直线分别交y轴于点G、F,求与满足的数量关系.
(1)、若点A坐标为 , 点C坐标为求其解析式;(2)、如图(1),已知抛物线的顶点D在直线:上滑动,且与直线交于另一点E,若的面积为 , 求此时点A的坐标;(3)、如图(2),在(1)的条件下,直线交抛物线于M,N两个不同的点,直线分别交y轴于点G、F,求与满足的数量关系. -
17、如图,在平面内将绕点逆时针旋转至 , 使 , 如果 , 那么旋转角度.

-
18、不透明袋子中有红球10个,黄球20个,还有一些蓝球,这些球除颜色外无其他差别,从袋子里随机摸出一个恰好是黄球的概率为 , 则蓝球有( )A、30个 B、60个 C、40个 D、20个
-
19、点关于原点对称的点的坐标是( )A、 B、 C、 D、
-
20、计算:(1)、;(2)、 .