相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、如图,已知等边中, , 点E、F分别为边上的两动点,且 , 连接 , 将的周长记为 . 那么与存在怎样的关系呢?
【问题探究】
(1)先将问题特殊化如图(2),当E点为中点时,直接写出与的等量关系 ;
(2)再探究一般情况如图(1),当E点为边上任意一点时,证明(1)中的结论仍然成立;
【问题拓展】
(3)如图(3),延长交于点G,若 , 直接写出的长度

-
2、某超市销售一种成本为20元/件的商品,若某个月的第x天(x为整数)的售价与销量的相关信息如下表所示:
第x天
售价(元/件)
日销售量(件)
设销售该商品的日销售利润为y元.
(1)、直接写出y与x的函数关系式;(2)、问销售该商品第几天时,日销售利润最大?最大日销售利润为多少元?(3)、如果超市每销售一件商品,就捐赠m元给希望工程,若仅在第15天销售利润额达到最大值,求m的取值范围. -
3、如图网格是由边长为个单位长度的小正方形组成,每个小正方形的顶点叫做格点,点A,B,C,D,P都是格点,请仅用无刻度的直尺完成下列作图,作图过程用虚线表示,作图结果用实线表示,
 (1)、如图1,画出关于点P中心对称的;(2)、如图2, , 交于点E,将线段平移至线段 , (点B对应点为E);(3)、在图3中,将绕点C顺时针旋转 , 其中旋转角 , 画出旋转后的 .
(1)、如图1,画出关于点P中心对称的;(2)、如图2, , 交于点E,将线段平移至线段 , (点B对应点为E);(3)、在图3中,将绕点C顺时针旋转 , 其中旋转角 , 画出旋转后的 . -
4、如图,是的内接三角形,点D是弧的中点,连接 , , .
 (1)、如图1,若 , 求的度数;(2)、如图2,若 , , 求 .
(1)、如图1,若 , 求的度数;(2)、如图2,若 , , 求 . -
5、已知抛物线中的 , 满足下表:
…
0
1
2
…
…
0
…
(1)、求抛物线的解析式;(2)、若 , 则自变量x的取值范围为 (直接写出结果)(3)、当时,抛物线与直线有交点,则的取值范围为 (直接写出结果) -
6、如图,在中, , 将绕着点A逆时针旋转得到 , 连接 , 求的长.

-
7、如图,在中,与的平分线交于点O,直线分别经过点、C,且 . 若直线关于对称的直线为 , 直线关于对称的直线 , 直线交于点 , 则的最大值为 .

-
8、抛物线交轴于点和 , 交轴于点 , 顶点为点 , 将其向左平移一个单位长度后图象关于轴对称.下列四个命题,其中真命题的序号是;
①;
②对于任意实数 , 总有;
③抛物线上有两点和 , 若 , 且 , 则;
④点关于抛物线对称轴的对称点为 , 点分别在轴和轴上,当时,四边形周长的最小值为 .
-
9、《九章算术》中记载:“今有户不知高、广,竿不知长短,横之不出四尺,从之不出二尺,邪之适出.”译文:今有门,不知其高、宽;有竿,不知其长短.横放,竿比门宽出4尺;竖放,竿比门高出2尺;斜放,竿与门的对角线长恰好相等,则门的对角线长为尺.
-
10、关于的方程的两实数根互为倒数,则两根之和为 .
-
11、点关于原点对称的点的坐标为 .
-
12、如图,是等边三角形外一点,连接 , , . 若 , , , 则三角形的面积为( )
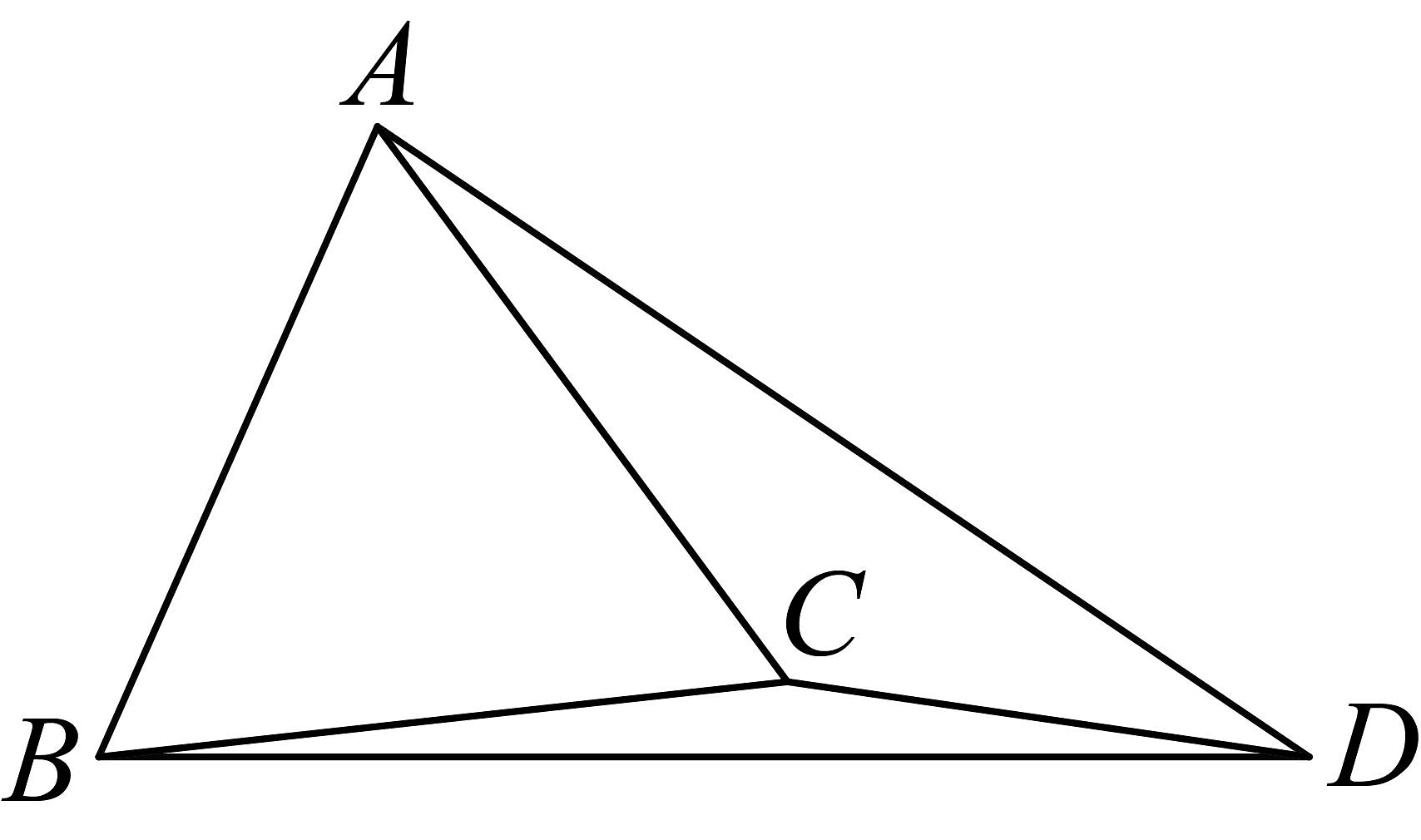 A、 B、 C、 D、
A、 B、 C、 D、 -
13、若函数的图象在的范围内与x轴没有公共点,则a的取值范围是( )A、 B、 C、 D、
-
14、如图,若是的直径,是的弦, , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、二次函数的顶点坐标是( )A、 B、 C、 D、
-
16、把方程化为的形式,则的值是( )A、7 B、3 C、 D、6
-
17、下列图形既是轴对称又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、一元二次方程的根的情况是( )A、无实数根 B、有两个相等实数根 C、有两不相等实数根 D、无法判断
-
19、一元二次方程的一次项系数、常数项分别为( ).A、 B、2,1 C、 D、3,1
-
20、拋物线向左平移8个单位,再向下平移9个单位后,所得抛物线的表达式是( )A、 B、 C、 D、