相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、已知与x成正比例,且时,(1)、求y与x之间的函数关系式;(2)、若点在该函数的图象上,求a的值.
-
2、如图,在中,是边上的高,平分 , 求的度数.

-
3、平面直角坐标系中,三角形的三个顶点的位置如图所示,点的坐标是 , 现将三角形平移,使点变换为点 , 点分别是的对应点.
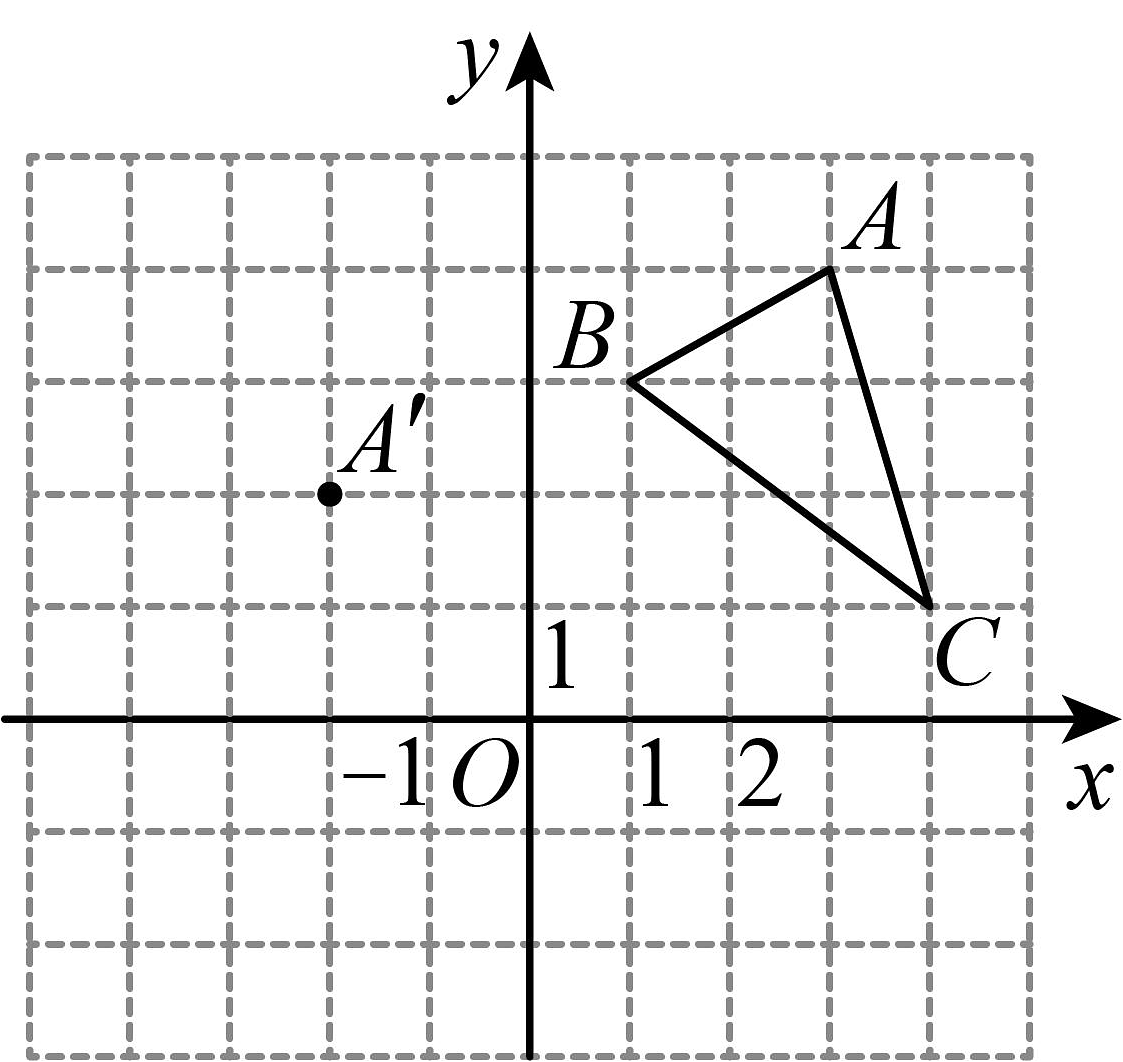 (1)、请画出平移后的三角形(不写画法),并直接写出点 的坐标:( )、( )(2)、若三角形 内部一点的坐标为 , 则点的对应点的坐标是( )
(1)、请画出平移后的三角形(不写画法),并直接写出点 的坐标:( )、( )(2)、若三角形 内部一点的坐标为 , 则点的对应点的坐标是( ) -
4、如图1,将一条长方形纸带沿折叠,设度.
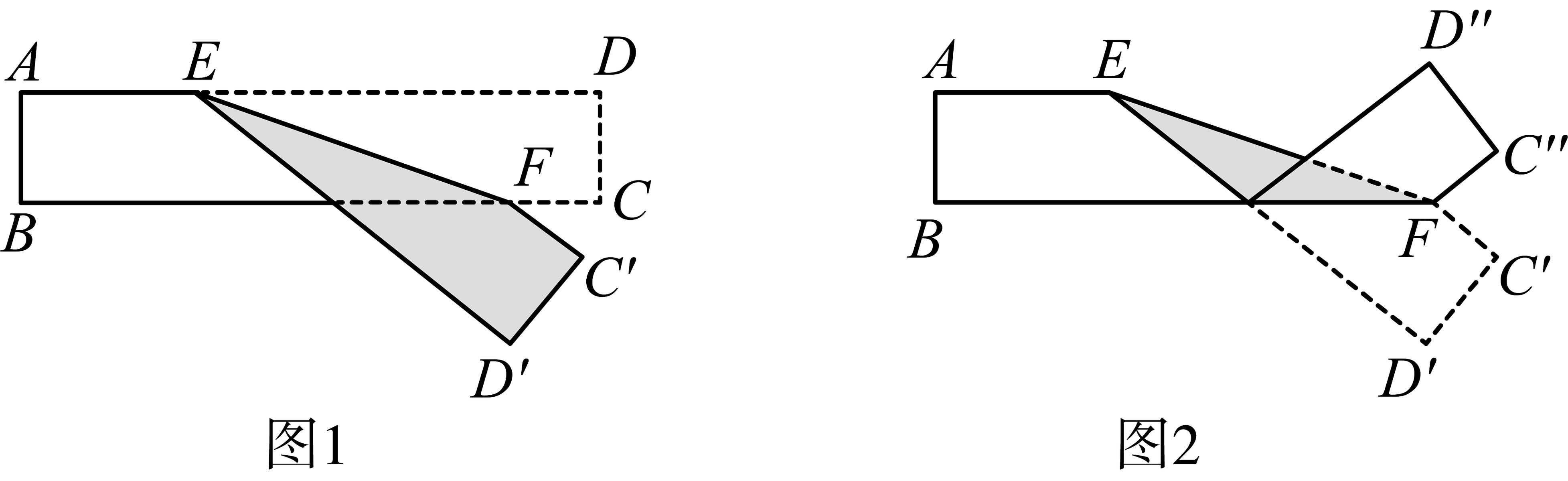
(1)若 , 则度;
(2)将图1纸带继续沿折叠成图2,则度.(用含的代数式表示)
-
5、某水果店销售某种水果,销售额y(元)与一次销售量与之间的函数关系如图所示.若王叔叔从该水果店一次性购买该种水果,需要付款元.

-
6、命题“有两个角相等的三角形是等腰三角形”的逆命题是(用“如果……那么……”的形式表示).
-
7、若直线向下平移3个单位长度后经过点 , 则m的值为 .
-
8、平面直角坐标系中,点到x轴的距离是 .
-
9、定义:平面直角坐标系中,若点A到x轴、y轴的距离和为1,则称点A为“和一点”.例如:点到x轴、y轴距离和为1,则点B是“和一点”,点也是“和一点”.一次函数的图象l经过点 , 且图象l上存在“和一点”,则k的取值范围为( )A、 B、 C、 D、
-
10、在下列条件中:①;②;③;④中,能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个
-
11、如图,在中,是边上的中线,E是的中点,连接 , 若的面积为 , 则阴影部分的面积是( )
 A、 B、 C、 D、条件不足,无法求出
A、 B、 C、 D、条件不足,无法求出 -
12、已知一次函数的图象经过三个点 , 则的大小关系( )A、 B、 C、 D、
-
13、已知一次函数的图象如图所示,则点所在的象限为( )
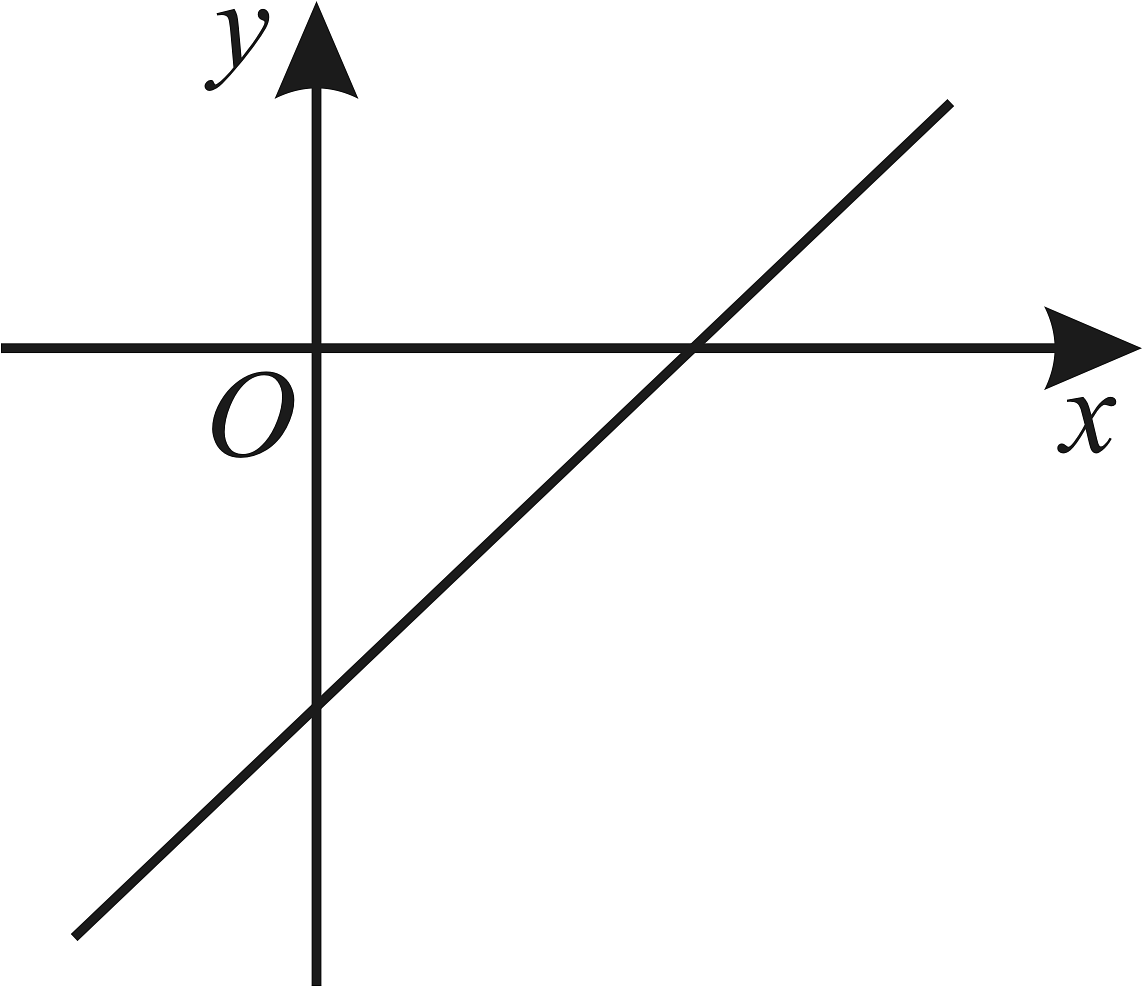 A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限 -
14、将点先沿x轴向左平移3个单位长度,再沿y轴向上平移2个单位长度后得到点 , 则的坐标为( )A、 B、 C、 D、
-
15、下列长度的三条线段,能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
16、已知:如图, , , , 则不正确的结论( )
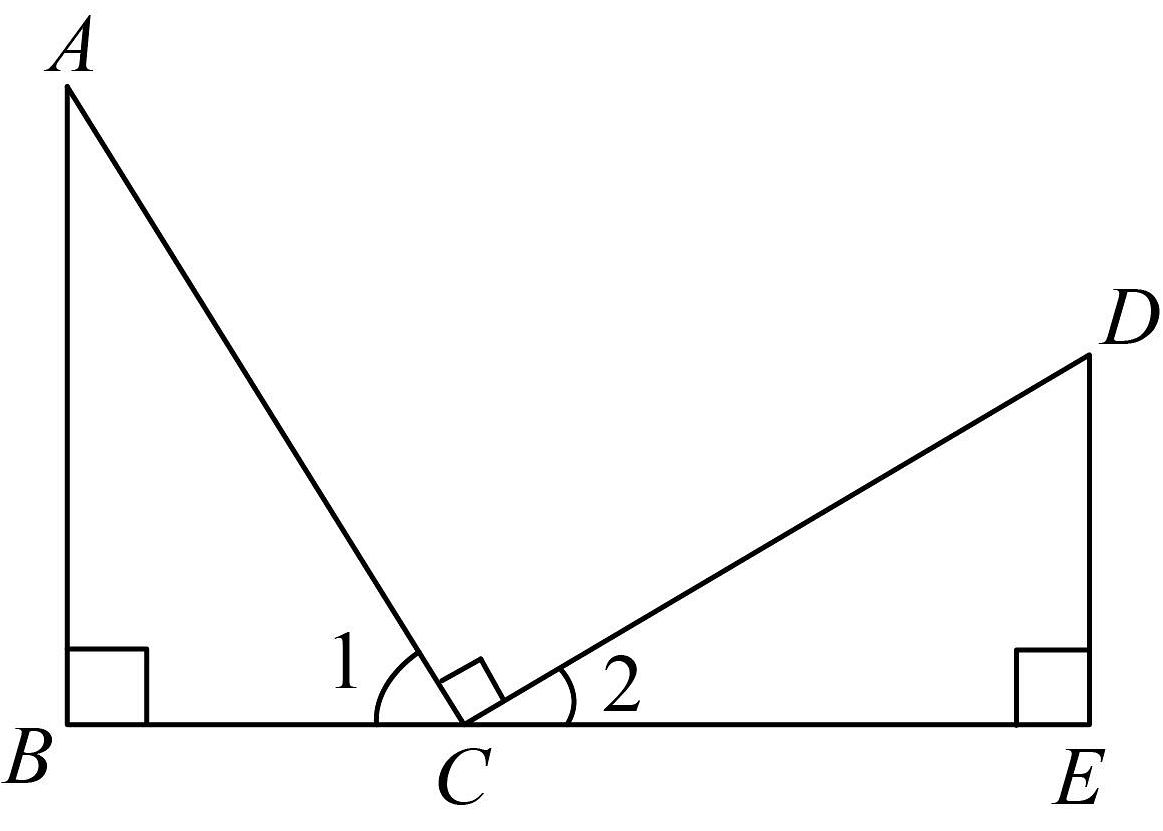 A、与互为余角 B、 C、 D、
A、与互为余角 B、 C、 D、 -
17、如图,中, , , 平分交于点 , 平分交于点 . 求证: .

-
18、某商店用3000元购进一批玩具,很快售完;第二次购进时,每件的进价提高了 , 同样用3000元购进的数量比第一次少了10件.(1)、求第一次每件的进价;(2)、若两次购进的玩具的售价均为80元/件,且全部售完,求两次的总利润.
-
19、如图,在中, , 于点D,过点C作 , , 连接并延长,交于点 .
 (1)、求的度数;(2)、求证:;(3)、求证: .
(1)、求的度数;(2)、求证:;(3)、求证: . -
20、已知关于的分式方程:(1)、当时,求此方程的解;(2)、当为何值时,此方程无解;