相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、如图,数轴上点分别表示有理数 , 若三个数的乘积为正数,这三个数的和与其中一个数相等,则b0.(选填“>”“<”或“=”)

-
2、﹣|﹣|的相反数是 .
-
3、小新玩“24 点”游戏,游戏规则是对数进行加、减、乘、除混合运算(每张卡片只能用一次,可以加括号)使得运算结果是 24 或-24.小新已经抽到前3 张卡片上的数字分别是
 , 若再从下列 4 张中抽出 1 张,则其中不能与前 3 张算出“24 点”的是( ) A、
, 若再从下列 4 张中抽出 1 张,则其中不能与前 3 张算出“24 点”的是( ) A、 B、
B、 C、
C、 D、
D、
-
4、三个有理数在数轴上表示的位置如图所示,则化简的结果是( )
 A、 B、 C、 D、0
A、 B、 C、 D、0 -
5、已知是最小的正整数,是最大的负整数,a、b互为相反数,x、y互为倒数,则的值是( )A、 B、 C、0 D、1
-
6、下列合并同类项正确的是( )A、 B、 C、 D、
-
7、下列式子书写正确的是( )A、 B、 C、 D、
-
8、正六边形的内角和是( )A、 B、 C、 D、
-
9、如图,和都是等边三角形,且点在一条直线上,连接和 , 交、于点 . 和相交于点 , 连接 .
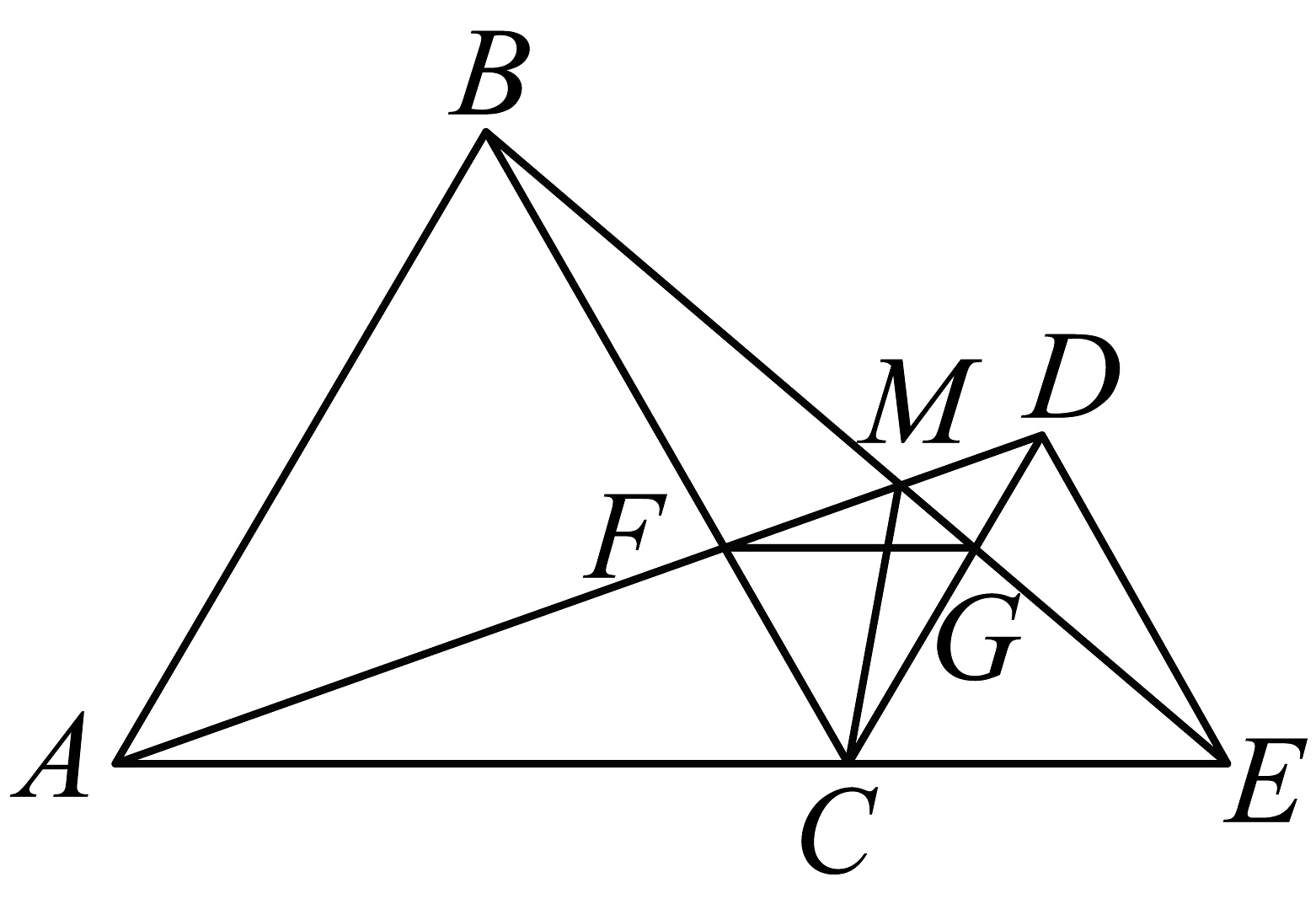 (1)、求证: .(2)、连接 , 请判断的形状,并说明理由.(3)、求证:平分
(1)、求证: .(2)、连接 , 请判断的形状,并说明理由.(3)、求证:平分 -
10、如图,在中, , , 的垂直平分线交于点 , 交于点 , 的垂直平分线交于点 , 交于点 , 连接 , , 求:
 (1)、的度数(2)、的周长
(1)、的度数(2)、的周长 -
11、已知:如图, , , .
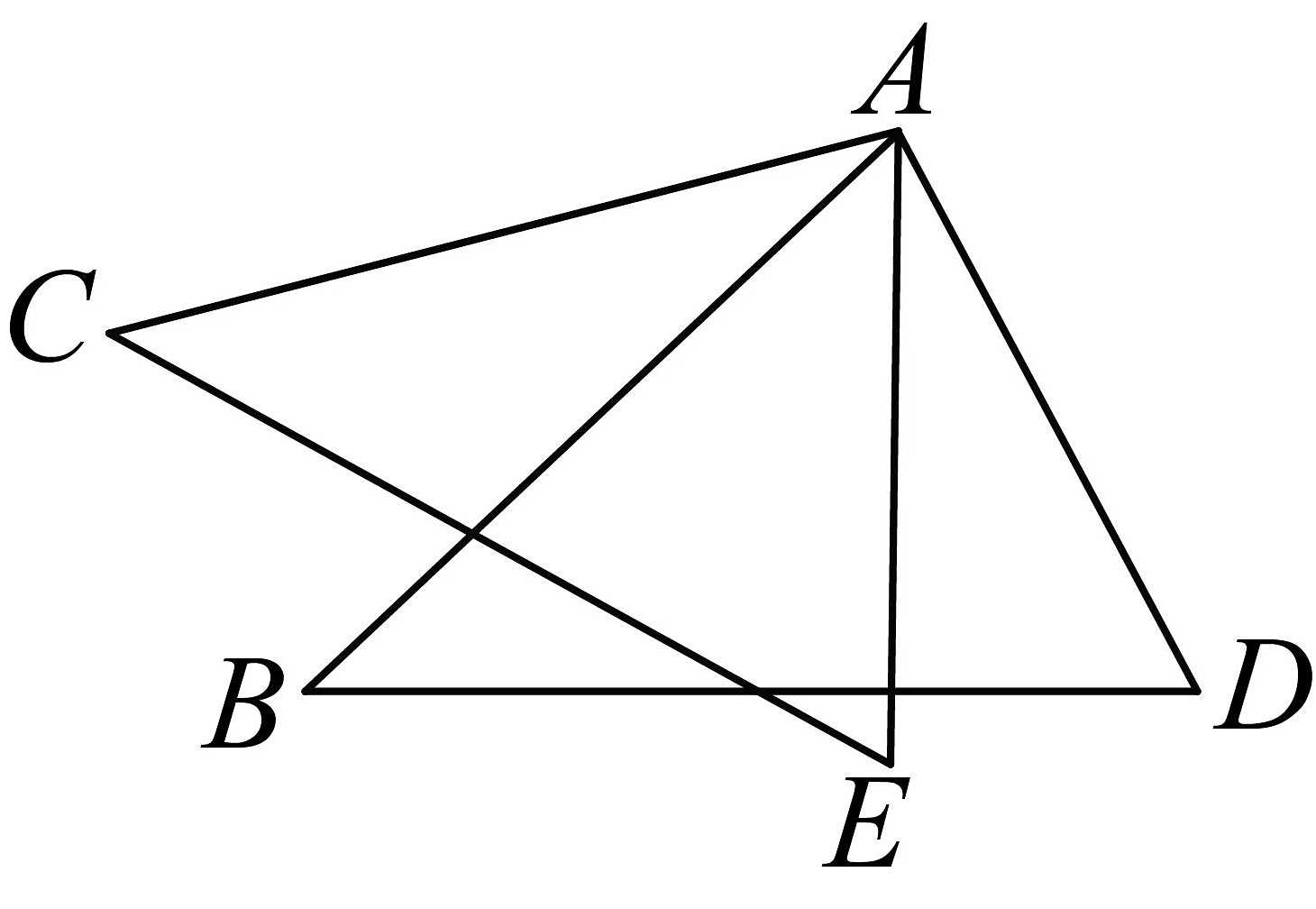
求证: .
-
12、如图,点B、F、C、E在一条直线上, , , . 求证: , .

-
13、若一个多边形内角和与外角和的比为9∶2,则这个多边形的边数是 .
-
14、在中, , 则
-
15、如图, .

-
16、如图,中, , , 垂直平分 , 则的周长是

-
17、如图,△ABC≌△DEC,点B的对应点E在线段AB上,若AB∥CD,∠DCA=40°,则∠B的度数是( )
 A、60° B、65° C、70° D、75°
A、60° B、65° C、70° D、75° -
18、一个多边形的内角和是 , 则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形
-
19、下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
20、在平面直角坐标系中,任意点到定点的距离等于到直线的距离,记点P的轨迹为抛物线 ,
 (1)、直接写出抛物线的解析式 ;(2)、将抛物线向右平移1个单位长度,再绕点旋转得到抛物线 , 抛物线与x轴交于A,B两点(A左B右),与y轴交于C点,R为抛物线上的动点,如图1,若以A、B、R、C为顶点的四边形为梯形,求点R的坐标;(3)、如图2,过点分别作直线:交(2)中的抛物线于点E,F,直线: ≠0)交抛物线于点G、H,点M、N分别为的中点,若直线与直线平行,求证:为定值,并求出该定值.
(1)、直接写出抛物线的解析式 ;(2)、将抛物线向右平移1个单位长度,再绕点旋转得到抛物线 , 抛物线与x轴交于A,B两点(A左B右),与y轴交于C点,R为抛物线上的动点,如图1,若以A、B、R、C为顶点的四边形为梯形,求点R的坐标;(3)、如图2,过点分别作直线:交(2)中的抛物线于点E,F,直线: ≠0)交抛物线于点G、H,点M、N分别为的中点,若直线与直线平行,求证:为定值,并求出该定值.