相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、解方程:(1)、;(2)、;(3)、;(4)、 .
-
2、如图,中,点D和点E分别是边 , 上的点,且 , , 若 , 则的面积为 .
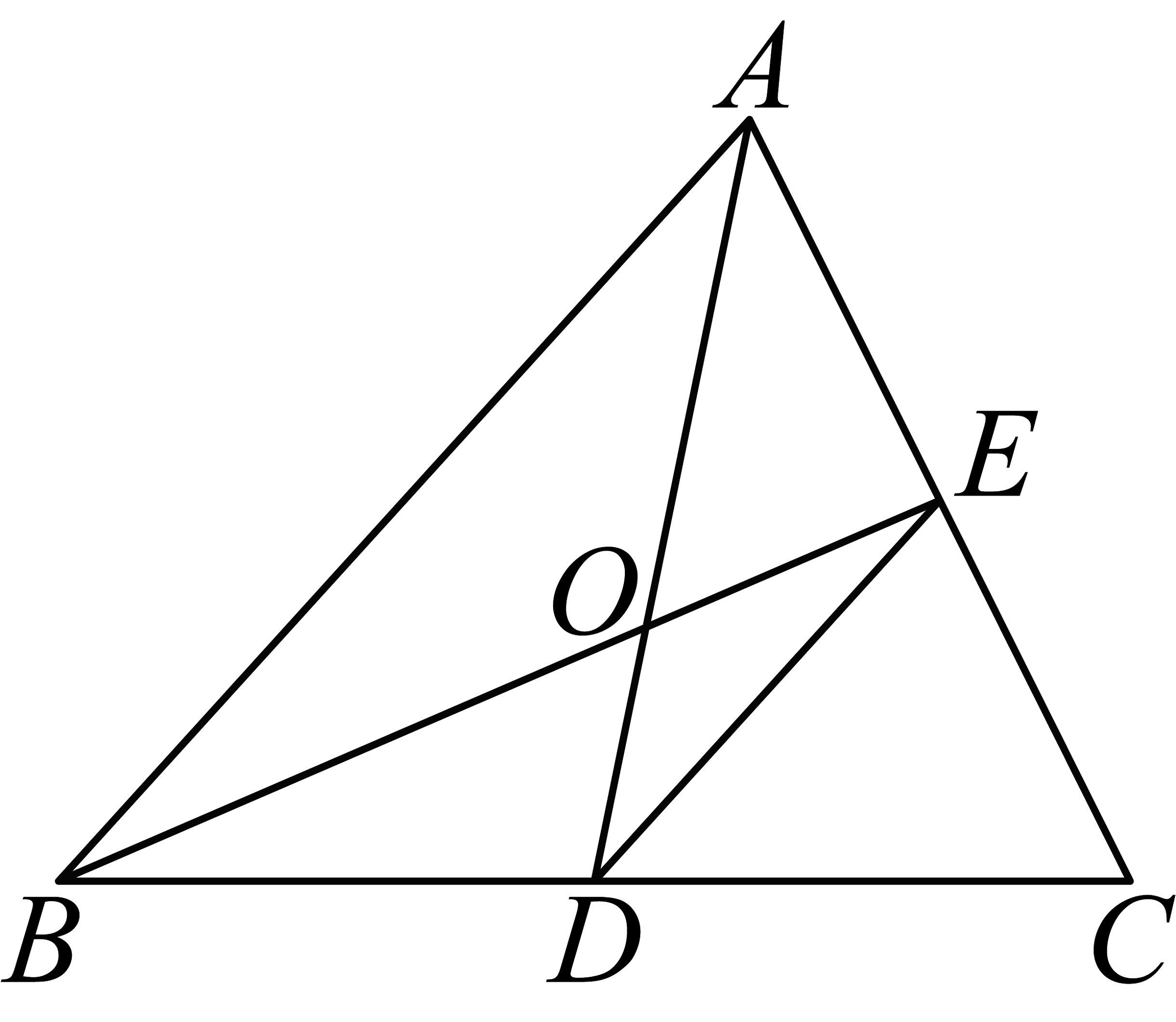
-
3、如图,在矩形中,点F在上,点E在上,把这个矩形沿折叠后,使点D恰好落在边上的点G处.若矩形面积为且 , , 则折痕的长为 .

-
4、如图所示,九(6)班数学兴趣小组利用标杆测量建筑物的高度,已知标杆高为 , 测得 , , 则建筑物的高是 .

-
5、若m是一元二次方程2x2+3x﹣1=0的一个根,则4m2+6m﹣2021= .
-
6、已知点C是线段的黄金分割点,且 , 若 , 则 .
-
7、如图,正方形中, , 点E在边上, , 将沿对折至 , 延长交边于点C,连接 , , 给出以下结论:;;; , 其中所有正确结论的个数是
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
8、某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
 A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是4
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是4 -
9、如图,平行四边形的周长为 , 、相交于点O,交于E,则的周长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、下列性质中正方形具有而菱形没有的是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、一条对角线平分一组对角
-
11、如图,在数轴上点A表示的有理数为–6,点B表示的有理数为6,点P从点A出发以每秒3个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒3个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒)
 (1)、求t=1时点P表示的有理数;(2)、求点P与点B重合时的t值;(3)、在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离;(用含t的代数式表示)(4)、当点P表示的有理数与原点的距离是3个单位长度时,直接写出所有满足条件的t值.
(1)、求t=1时点P表示的有理数;(2)、求点P与点B重合时的t值;(3)、在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离;(用含t的代数式表示)(4)、当点P表示的有理数与原点的距离是3个单位长度时,直接写出所有满足条件的t值. -
12、阅读材料:我们知道, , 类似地,我们把看成一个整体,则 . “整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.(1)、尝试应用:
把看成一个整体,合并的结果是 .
(2)、已知 , 求的值;(3)、拓展探索:已知 , , , 求的值.
-
13、已知: , .(1)、求和的值;(2)、若 , 求的值.
-
14、计算:(1)、(2)、
-
15、细菌是靠分裂进行生殖的,也就是1个细菌分裂成2个细菌,分裂完的细菌长大以后又能进行分裂.例如,图中所示为某种细菌分裂的电镜照片,显示这种细菌每20分钟就能分裂一次.1个这种细菌经过3个小时可以分裂成个细菌.
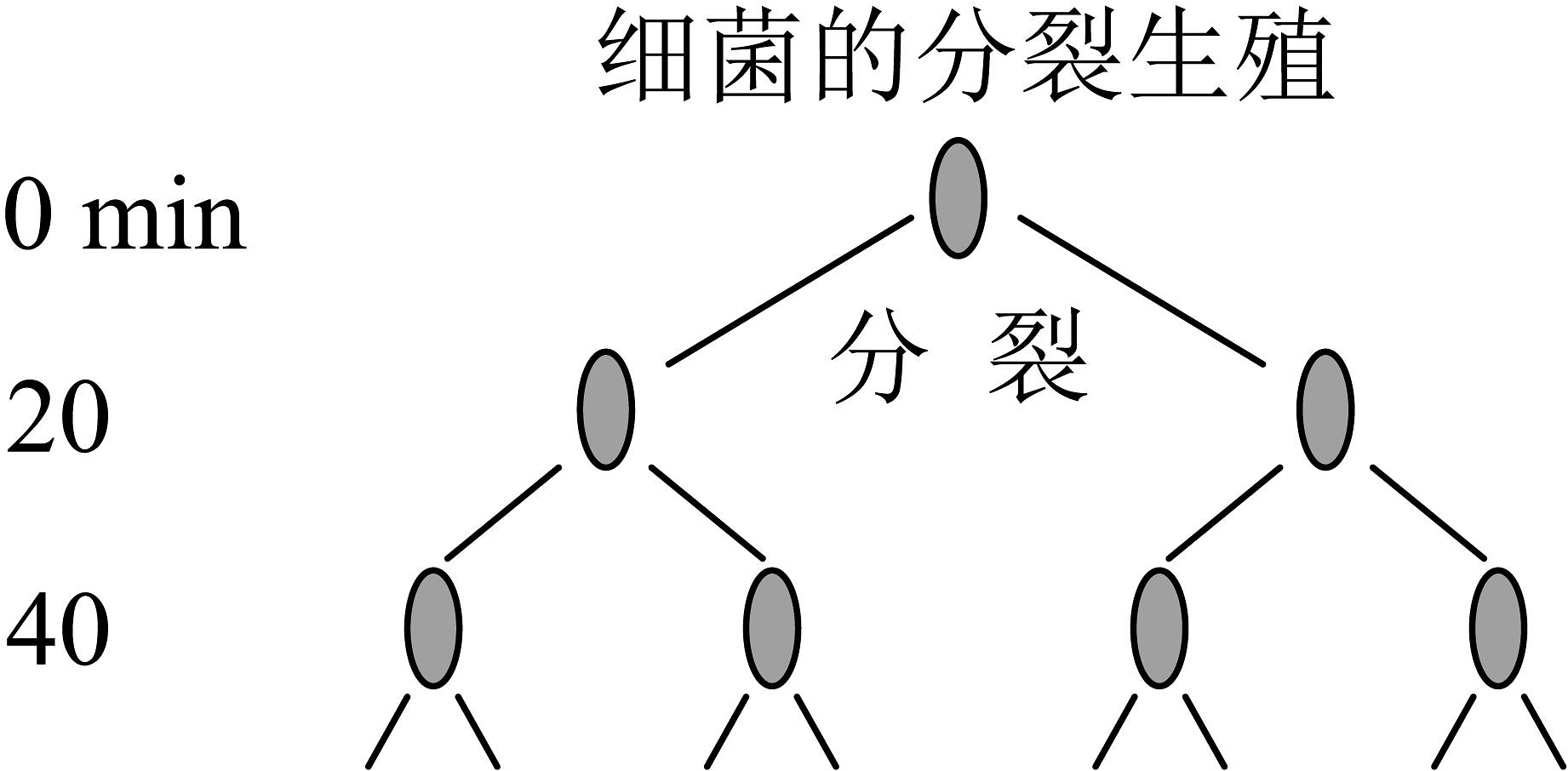
-
16、同学们都熟悉“幻方”游戏,现将“幻方”游戏稍作改进变成“幻圆”游戏,将 , , , , , , , 分别填入图中的圆圈内,使横、竖以及内外两圈上的个数字之和都相等,则的值为( )
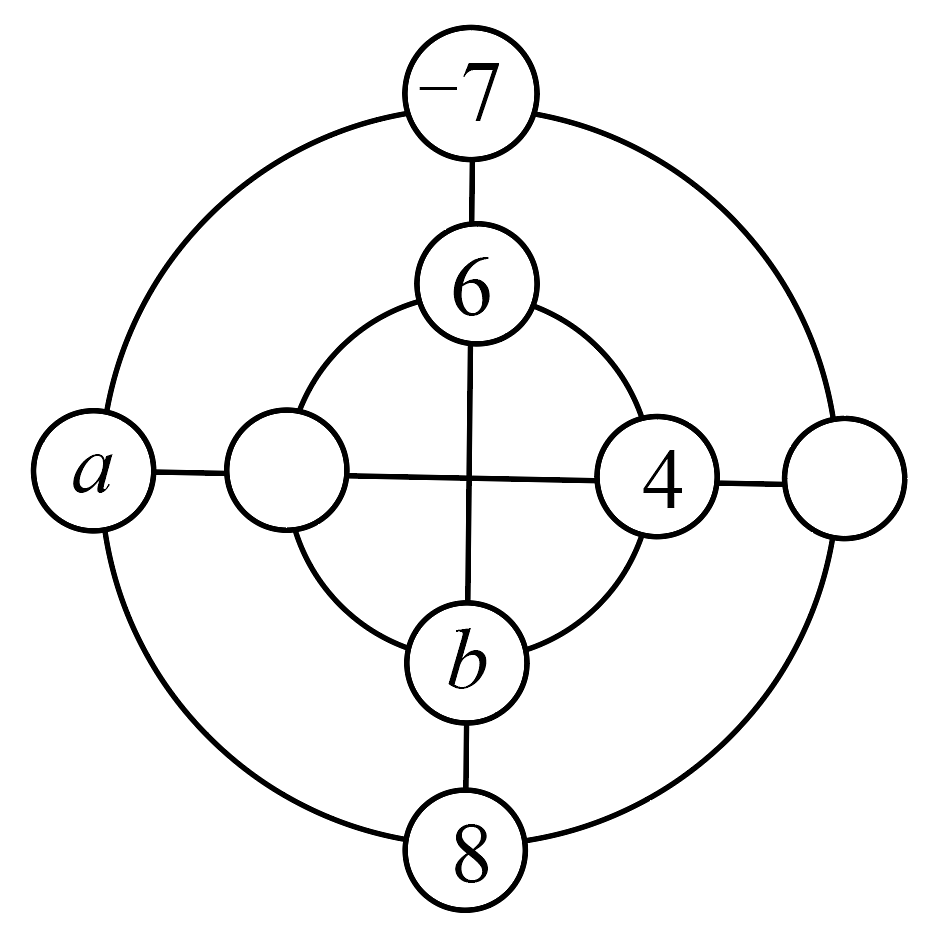 A、 B、 C、或 D、或
A、 B、 C、或 D、或 -
17、年春节前,一轮雨雪降温席卷黔北地区,某地一周最低气温如下表,其中最低气温出现在( )
日期
周日
周一
周二
周三
周四
周五
周六
气温()
A、周一 B、周二 C、周五 D、周六 -
18、年月日时分.“嫦娥六号”着陆器在月球背面预定着陆区域成功着陆.月球与地球之间的距离约为千米,将用科学记数法表示为( )A、 B、 C、 D、
-
19、如图,在平面直角坐标系中,O为坐标原点.三角形ABC的边BC在石轴上,点B的坐标是(-5,0),点A在y轴的正半轴上,点C在x轴的正半轴上,它们的坐标分别为A(0,m)、C(m-1,0),且OA+OC=7,动点P从点B出发,以每秒2个单位的速度,沿射线BO运动.设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连结PA,当P沿射线BO匀速运动时,是否存在某一时刻,使三角形POA的面积是三角形ABC面积的?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.

-
20、阅读下列一段文字,然后回答下列问题.已知在平面内两点、 , 其两点间的距离同时,当两点所在的直线在坐标轴或平行于坐标轴时,两点间距离公式可简化为或 .(1)、已知、 , 试求A、B两点间的距离;(2)、已知A、B在平行于y轴的直线上,点A的纵坐标为6,点B的纵坐标为 , 试求A、B两点间的距离.(3)、已知一个三角形各顶点坐标为、、 , 请判定此三角形的形状,并说明理由.(4)、已知一个三角形各顶点坐标为、、 , 请判定此三角形的形状,并说明理由.