相关试卷

1、某市民用电费的价格是0.538元/千瓦时。设用电量为x千瓦时，应付电费为y元，则y关于x的函数表达式是。当x=40时，函数值是，它的实际意义是。若某用户的用电量为65千瓦时，则该用户应付电费为元。

查看解析
2、骑自行车30分钟，热量消耗W(焦)与体重x(千克)之间的函数关系如图所示。

(1)、请说出体重为30千克和50千克时，热量消耗W(焦)的值。

(2)、当 W=336焦时，自变量x的值约为多少?这个值的实际意义是什么?

查看解析
3、某市居民生活用水的价格是2.9元/立方米。设某户居民这个月的用水量为n立方米，应付水费为m元。在这个问题中，m关于n的函数表达式是。当n=15时，函数值是，这一函数值的实际意义是。

查看解析
4、北仑港某一天潮汐高度随时间变化如图所示。
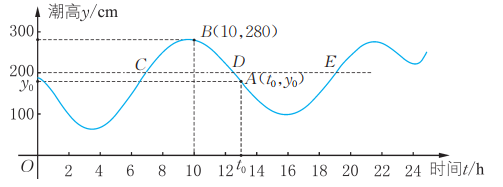
请观察图象，解答下列各题：

(1)、潮高y(cm)是时间t(h)的函数吗? 为什么?

(2)、求当t=10时的函数值，并说明函数值的实际意义。

(3)、一天内，有几次潮高为200cm?

查看解析
5、如图是传说中的一张藏宝图，藏宝人生前通过建立直角坐标系(以南北方向为纵轴，东西方向为横轴)画出这幅藏宝图。现在我们只知道图上两块大石头的坐标为A(1，2)，B(8，9)，而藏宝地的坐标为(5，7)。在地图上找到宝藏的位置，并表示出来。

查看解析
6、如图，在梯形ABCD中，AB∥CD，BC⊥AB，AB=5，BC=4，CD=3。在原图中建立适当的直角坐标系，并写出各顶点的坐标。

查看解析
7、某风景区中古塔、飞瀑、笔峰、望夫石四个景点的位置依次在一个边长为4km的正方形的四个顶点上(如图)。试选取适当的比例，建立适当的坐标系，确定四个顶点的坐标，并在直角坐标系中标出它们的位置。

查看解析
8、如图，在△ABC中，AC=BC=2cm，∠C=Rt∠。分别按下列条件建立直角坐标系，并确定△ABC各顶点的坐标。

(1)、使AB的中点为原点，AB边在x轴上。

(2)、使点C为原点，边AB的中垂线为y轴。

查看解析
9、已知某镇的镇政府、镇中心小学、镇文化礼堂的位置如图。用线段连结这三个地点，恰好构成一个等边三角形，且边长为2k m。试选取适当的比例，建立直角坐标系，在直角坐标系中画出这三个地点的位置，并标出坐标。

查看解析
10、已知长方形ABCD的长为2，宽为1。以AB所在的直线为x轴，AB的中点为原点，建立直角坐标系，如图。求长方形各个顶点的坐标。

查看解析
11、一个四边形的形状和尺寸如图所示。建立适当的直角坐标系，在坐标系中作出这个四边形，并标出各顶点的坐标。

查看解析
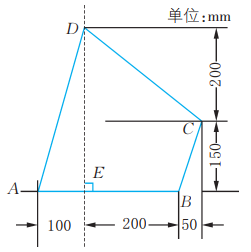
12、对于正方形ABCD，建立如图的直角坐标系。写出A，B，C，D各顶点的坐标。如果把x轴往下平移2个单位长度，那么A，B，C，D各顶点坐标在新坐标系中将怎样变化?

查看解析
13、如图是画在方格纸上的我国著名的水泊梁山的旅游景点简图。

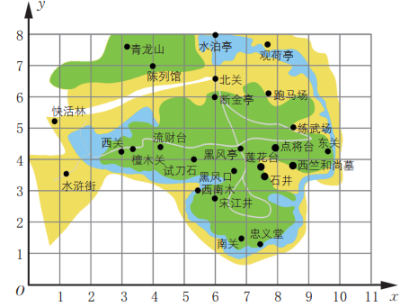(1)、分别写出忠义堂、黑风亭、快活林、练武场的坐标(精确到0.1)。

(2)、点(6，8)，(6.6，3.6)，(7.9，4.4)所表示的地点分别是什么?

查看解析
14、已知点A(2，15)，B( $\sqrt{5}$ ， 3)，C(-5，2)， $D (- 0.5, \sqrt{7}) 。$ 。判断这些点中，哪些在阴影区域内，哪些不在阴影区域内。

查看解析
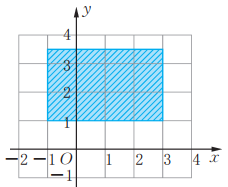
15、根据图中各点的位置填表。
点
坐标
所在象限或坐标轴
A

B

C

D

E

F

G

O

查看解析
16、指出图中点A，B，C，D，E，F，G分别在哪一个象限内，并写出各点的坐标。

查看解析
17、在如图所示的平面直角坐标系内画出下面这些点：M(-1，0)，N(2，2)，P(1.5，-1.5)，Q(4，-4)。

查看解析
18、如图。

(1)、写出图中六边形各个顶点的坐标。它们各在哪个象限内或坐标轴上?哪些点的横坐标相同?哪些点的纵坐标相同?

(2)、作出点G(-2，-1)，H(-3，5)，M(0，3)，N(5，-2)，并判断这些点中哪些在六边形内，哪些在六边形外。

查看解析
19、

(1)、如图，写出直角坐标系内点M，N，L，O，P的坐标。

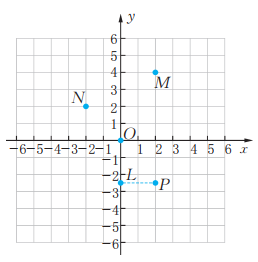(2)、在直角坐标系内画点A(2，4)，B(5，2)，C(-3.5，0)，D(-3.5，-2)。

查看解析
20、通过报刊、互联网等途径查找资料，写一段涉及多个量的短文，找出其中的变量和常量，并说明你的理由。

查看解析

上一页 270 271 272 273 274 下一页跳转

点	坐标	所在象限或坐标轴
A
B
C
D
E
F
G
O