相关试卷
- 2017-2018学年人教版数学七年级下册同步训练： 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练：19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练： 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练： 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练：19.2.3《一次函数与方程、不等式》
-
1、某批服装的进价为每件200元，商店标价每件300元出售。现商店准备将这批服装降价出售，但要保证毛利润率不低于5%。问：售价最低可按标价的几折?
-
2、写出两个解集为x>8的不等式。
-
3、 解不等式0.5x-3>-14-2.5x，把解集表示在数轴上，并求出满足不等式的最小负整数和最小正整数。
-
4、解下列不等式，并把解集表示在数轴上。(1)、(2)、 3x-1≥2x+4；(3)、 5x-2>11x+3。
-
5、 填空：(1)、 不等式3x>1的解集是 ， 不等式-x>3的解集是；(2)、 不等式x+1≥3的解集是 ， 不等式2<x-1的解集是；(3)、一个不等式的解集在数轴上表示如图，则这个不等式的解集是。
-
6、解不等式 把解集表示在数轴上，并求出满足不等式的正整数解。
-
7、下列不等式的解法正确吗?如果不正确，请改正。(1)、 - 2x<-4。
解：两边都除以－2，得x＜2。(2)、x+1>2x-3。解：移项，得4＞x，即x＞4。 -
8、解下列不等式，并把解集表示在数轴上。(1)、 1-x>2；(2)、(3)、 6x-1>9x-4。
-
9、解不等式7x-2≤9x+3，在数轴上表示解集，并求出不等式的负整数解。
-
10、解下列不等式，并在数轴上表示解集。(1)、 4x<10；(2)、
-
11、某城市12个月平均最高气温t(℃)与月份的函数关系如图。
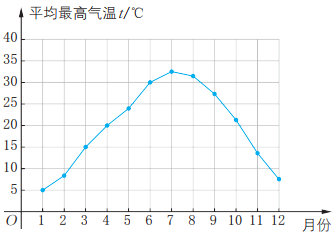(1)、求该城市1月，7月的平均最高气温。(2)、分析该城市1月到12月的气温变化情况，并说明哪个月最冷、哪个月最热。 -
12、 如图，设正方形的面积为y(cm2)，边长为x(cm)。
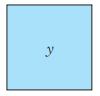(1)、求y关于x的函数表达式，并求自变量x的取值范围。(2)、 分别求当x=5，10时，函数y的值。 -
13、专家建议，每人每天的食盐摄入量以不超过5g为宜。为控制食盐摄入，某单位向员工发放一个小盐勺(容量为1g)。设家庭人数为x，家庭每天应摄入食盐勺数的最大值为y。(1)、写出y与x的函数关系式和自变量x的取值范围。(2)、当x=3时，y的值是多少?说明此时函数值的实际意义。
-
14、一列行驶中的火车的速度为每小时160千米，用t(时)表示行驶的时间，s(千米)表示行驶的路程。其中常量是 ， 变量是 ， s关于t的函数表达式是。当t=2.5时，函数s的值是 ， 它的实际意义是。
-
15、解一元一次不等式组
-
16、解一元一次不等式组
-
17、下图是某水库的库容曲线图，其中x表示水库的平均水深(米)，V表示水库的库容(万立方米)。根据图象回答下面的问题。
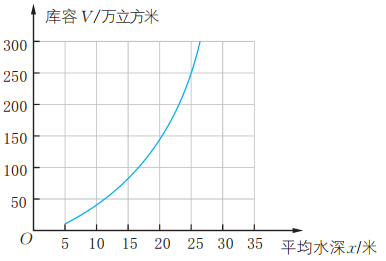(1)、这个函数反映了哪两个变量之间的关系?(2)、 填表：x/米
5
10
15
20
25
V/万立方米
(3)、当平均水深取5m至25m之间的一个确定的值时，相应的库容V确定吗?(4)、库容V可以看成平均水深x的函数吗?(5)、求当x=18时的函数值，并说明它的实际意义。 -
18、某小区临时停车收费规则如下：半小时内(含半小时)收费5元；超过半小时，每小时收费10元(不足1小时按1小时计)；每天不超过40元。如果停车时间为x(h)，停车费为y(元)。(1)、y是关于x的函数吗?为什么?(2)、分别求当x=0.5，1，3.4，6时的函数值，并说明它们的实际意义。
-
19、已知△ABC的底边BC上的高线长是6cm。当BC的长改变时，三角形的面积也将改变。(1)、 若△ABC的底边BC的长为x(cm)，则△ABC的面积y(cm2)可表示为。(2)、当底边BC的长x从12cm变化到3cm时，三角形的面积y从cm2变化到cm2。
-
20、求下列函数当x=4时的函数值。(1)、(2)、