相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、已知:如图,AB∥CD,∠A=∠C。求证:AD=BC。

-
2、阅读下面一段文字:
泰勒斯(Thales,约前624~前547)是古希腊哲学家。相传“两个角及其夹边对应相等的两个三角形全等”就是由泰勒斯首先提出的。泰勒斯利用这个判定三角形全等的依据求出了岸上一点到海中一艘船的距离。

如图,A是观测点,船P在A的正前方。过A作AP的垂线l,在垂线l上截取任意长AB,O是AB的中点。观测者从点B沿垂直于AB的BK方向走,直到点K和船P、点O在一条直线上,那么BK的长度即为船离岸的距离。
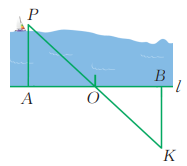
请给出证明。
-
3、已知:如图, 。求证: .
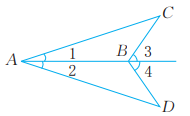
-
4、根据所给条件,下列各题中的两个三角形一定全等吗?若不一定,请举出反例;若一定,说明理由。(1)、 △ABC和△MNP中,∠A=∠M,AB=MN;(2)、△RST和△XYZ中,∠R=∠X,∠S=∠Y,∠T=∠Z。
-
5、如图,在. 和 中,点B,E,C,F在同一条直线上。下面给出四个论断:
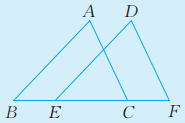
①; ②
③∠ABC=∠DEF; ④BE=CF。
任选三个作为已知条件,余下一个作为结论,可得到几个命题?其中真命题有几个?分别给出证明。
-
6、 已知:如图,AD平分. 求证:
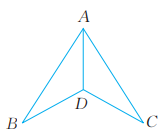
-
7、 已知:如图,点D,E分别在AC,AB上, 求证:AE=AD。
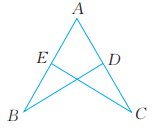
-
8、已知:如图,AC与DB相交于点P,∠1=∠2,∠ABC=∠DCB。求证:AP=DP,BP=CP。
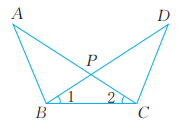
-
9、已知:如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',BC=B'C'。求证:△ABC≌△A'B'C'。

-
10、一块三角形玻璃被摔成三片(如图)。如果只带上其中的一片,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃,那么你知道应带哪一片碎玻璃吗?请说明理由。

-
11、 如图,已知四边形ABDC的面积为14,AD平分∠BAC,AB+AC=7。求点D到AB的距离。
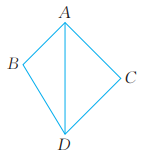
-
12、 如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=2CD。若点D到AB的距离DE为5.6cm,求BC的长。

-
13、 已知:如图,AB平分∠CAD,∠C=∠D=90°。求证:BC=BD。
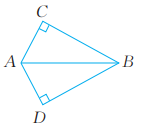
-
14、证明:三角形的两条角平分线的交点到各边的距离相等。
-
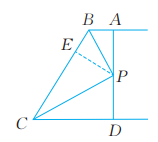
15、已知:如图,AB∥CD,PB,PC分别平分∠ABC,∠DCB,AD过点P,且与AB垂直。求证:PA=PD。
-
16、任意作一个角,记为∠BAC,P是∠BAC的平分线上的一点,PB⊥AB于点B,PC⊥AC于点C。比较PB和PC的大小,并证明你的结论。

-
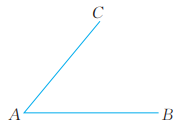
17、已知∠BAC(图),用直尺和圆规作 的平分线AD。
-
18、从报刊、图书、网络等搜集一些能用一元一次不等式解决的问题,分析其中的数量关系,建立不等式模型加以解决。
-
19、两根木棒的长分别是5cm和7cm。要选择第三根木棒,将它们首尾相接钉成一个三角形。若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种?
-
20、小聪用100元钱购买笔记本和黑色中性笔共30件。已知每本笔记本5元,每支黑色中性笔2元。问:小聪最多能买多少本笔记本?