相关试卷
- 2017-2018学年人教版数学七年级下册同步训练： 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练：19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练： 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练： 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练：19.2.3《一次函数与方程、不等式》
-
1、如图，已知△ABC和直线m。以直线m为对称轴，求作以点A，B，C的对称点A'，B'，C'为顶点的△A'B'C'。
-
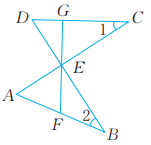
2、 已知：如图，BD⊥AC，E为垂足，△ABE的中线FE的延长线交CD于点G，∠1=∠2。求证：△CGE是直角三角形。
-
3、 已知：如图，A，B，D在同一条直线上，∠A=∠D=90°，AC=BD，∠1=∠2。求证：△BEC是等腰直角三角形。
-
4、 如图，AB∥CD，AC平分∠BAD，BD平分∠ADC，AC和BD交于点E。写出图中所有的直角三角形(不要求证明)。
-
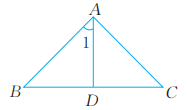
5、 如图，在△ABC中，AB=AC，AD⊥BC于点D，∠1=∠C。求∠B，∠C，∠BAC的度数。
-
6、根据下列条件判断△ABC是不是直角三角形，并说明理由。(1)、 ∠B=50°，∠C=40°；(2)、 ∠B=∠C=45°；(3)、 ∠A，∠B，∠C的度数比为5：3：2。
-
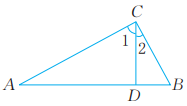
7、 已知：如图，在△ABC中，D是AB上一点，∠1=∠B，∠A=∠2。求证：△ABC是直角三角形。
-
8、在如图的方格纸上画三个互不全等的直角三角形，使其顶点都在格点上，并用符号“Rt△”和字母将它们表示出来。
-
9、已知：如图，在△ABC中，CD是AB边上的中线，
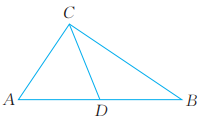
求证：△ABC是直角三角形。
-
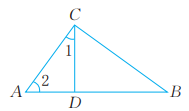
10、根据下列条件判断△ABC是不是直角三角形，并说明理由。(1)、 有一个外角为90°；(2)、 ∠A=36°，∠B=54°；(3)、 如图，∠1与∠2互余，∠B=∠1。
-
11、 已知：如图，AB=AD，AC=AE，∠BAC=∠DAE=90°。求证：
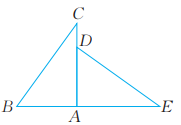(1)、∠C=∠E。(2)、 ED⊥BC。 -
12、 已知：如图，AB∥DE，AB=DE，点B，E，C，F在一条直线上，且BE=CF。求证：AC∥DF。
-
13、 已知：如图，AC=BD，∠CAB=∠DBA。求证：
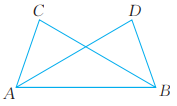(1)、 △ABC≌△BAD。(2)、 BC=AD，∠C=∠D。 -
14、已知：如图， 。求证：
-
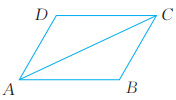
15、如图，已知线段a，c和 ， 用直尺和圆规作 使
-
16、为了测量池塘两端A，B间的距离，小红在地面上选择了点O，D，C，使 且点A，O，C和点B，O，D分别都在一条直线上。 小红认为只要量出点D，C间的距离，就能知道点A，B间的距离。你认为正确吗?请说明理由。
-
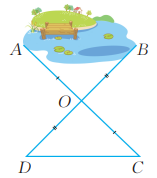
17、 已知：如图，AB=AC，点D，E分别在AC，AB上，且AD=AE。
求证：BD=CE(填空)。
证明：在和 ▲ 中，
因为 ，
所以 ▲ ≌ ▲ ( )，
所以BD=CE ( ) 。
-
18、已知：如图，AB=DB，BC=BE，∠1=∠2。求证：∠C=∠E。
-
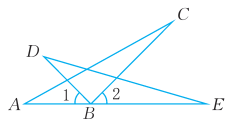
19、如图，把两根钢条AA'，BB'的中点钉在一起，可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
-
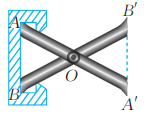
20、已知：如图，AC与BD相交于点O，且OA=OC，OB=OD。
求证：△AOB≌△COD。