相关试卷

1、等腰三角形ABC的周长为10，底边BC长为y，腰AB长为x。

(1)、求y关于x的函数表达式。

(2)、写出自变量x的取值范围。

(3)、当腰长AB=3时，底边BC的长为多少?

查看解析
2、老王和小张在同一家公司工作。老王每月的工资比小张高，但不到他的两倍。新一年开始时，公司给他们同时加薪10%，问：加薪后老王的工资仍不到小张的两倍吗?如果每人各加薪500元呢?请说明理由。

查看解析
3、若x<y，且(a-3)x>(a-3)y，求a的取值范围。

查看解析
4、若x>y，比较2-3x与2-3y的大小，并说明理由。

查看解析
5、某品牌计算机键盘的单价在60元至70元之间(包括60元和70元)，买3个这样的键盘需要多少钱(用适当的不等式表示)?

查看解析
6、按下列条件，写出仍能成立的不等式：

(1)、 $\sqrt{7} > \sqrt{5} ，$ 两边都减去 $\sqrt{5} ，$ 得；

(2)、 $x + \frac{1}{2} < 0 ，$ 两边都加上 $(- \frac{1}{2}) ，$ 得；

(3)、 $\frac{9 m}{7} > \frac{4 n}{3} ，$ 两边都乘21，得；

(4)、 - 0.9<-0.3，两边都除以(-0.3)，得；

(5)、 $- \frac{8}{7} x \leq 1 ，$ 两边都乘 $(- \frac{7}{8}) ，$ 得。

查看解析
7、选择适当的不等号填空：

(1)、若a>b，则ba；

(2)、若a>b，且b>c，则ac。

查看解析
8、比较等式与不等式的基本性质，它们有什么异同点?
例如，等式是否有与不等式的基本性质1类似的传递性?不等式是否有与等式的基本性质类似的移项法则?你可以用列表的方式进行对比。
(请与你的同伴交流)
表
等式
不等式
a=b，b=c⇒
a<b，b<c⇒

…
…

查看解析
9、选择适当的不等号填空：

(1)、若 $a - b > 0 ，$ ，则ab；

(2)、若 $a > - b ，$ 则 $a + b_0 ；$

(3)、若 $- a < b ，$ 则 $a_- b ；$

(4)、若 $- a > - b ，$ 则 $2 - a_2 - b ；$

(5)、若 $a > 0 ，$ 且 $(1 - b) a < 0 ，$ ，则b1；

(6)、若 $a < b ， b < 2 a - 1$ ，则a2a-1。

查看解析
10、填空：

(1)、若x+1>0，两边都加上-1，得(依据：)；

(2)、若 $2 x > - 6 ，$ ，两边都除以2，得(依据：)；

(3)、若 $- \frac{1}{3} x \leq \frac{1}{2} ，$ 两边都乘 $- 3$ ，得(依据：)。

查看解析
11、已知a<0，试比较2a与a的大小。

查看解析
12、选择适当的不等号填空：

(1)、因为01，所以aa+1(不等式的基本性质2)；

(2)、因为 ${(a - 1)}^{2}$ 0，所以 ${(a - 1)}^{2} - 2$ -2(不等式的基本性质2)。

查看解析
13、已知：如图，AD是BC的垂直平分线，DE⊥AB于点E， $D F ⟂ A C$ 于点F。求证：DE=DF。

查看解析
14、已知：如图，AD垂直平分BC，D为垂足。DM⊥AC，DN⊥AB，M，N分别为垂足。求证：DM=DN。

查看解析
15、有一段关于古代藏宝图的记载(如图)：“从赤石向一棵杉树笔直走去，恰好在其连线中点处向右转90°前进，到达唐伽山山脚的一个洞穴，宝物就在洞穴中。”怎样根据这段记载找到藏宝洞穴的位置?在图上标出藏宝洞穴的位置。

查看解析
16、已知：如图，直线l和直线m分别是线段AB和线段AC的垂直平分线，O为交点。求证：点O到点A，B，C的距离相等。

查看解析
17、如图，在△ABC中，AB，AC的垂直平分线分别交BC于点D，E。已知△ADE的周长为12cm，求边BC的长。

查看解析
18、如图，已知△ABC，用直尺和圆规作中线CD。

查看解析
19、如图，已知直线l和直线外一点A。用直尺和圆规作过点A的直线l的垂线。

查看解析
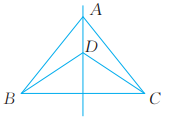
20、已知：如图，直线AD是线段BC的垂直平分线，连结AB，AC，DB，DC。求证：△ABD≌△ACD。

查看解析

上一页 262 263 264 265 266 下一页跳转

等式	不等式
a=b，b=c⇒	a<b，b<c⇒




…	…