相关试卷

1、对于函数y=-2x+5，当-1<x<2时，<y<。

查看解析
2、某公司每月生产A，B两种型号的口罩共20万只，且所有口罩当月全部售出。两种型号口罩的成本、售价如下表。
口罩型号
每只成本/元
每只售价/元
A
1
1.5
B
3
6

(1)、设该公司每月生产A型口罩x万只，月毛利润为y万元，试写出y关于x的函数表达式。

(2)、该公司计划5月投入口罩生产的成本不超过28万元，且B型口罩每只售价降低2元，问：应该怎样安排A，B两种型号口罩的产量，使得当月销售毛利润最大?并求出最大毛利润。

查看解析
3、已知一次函数y= kx+b(k<0)的系数k，b满足3k+b=0，点>(-1，y₁)，(4，y₂)在这个函数的图象上，试比较y₁ ， 0，y₂三个数的大小。

查看解析
4、对于下列两个函数，设当x=x₁时，y=y₁；当 $x = x_{2}$ 时， $y = y_{2} 。$ 用“>”或“<”填空。
对于函数y=2x，若. $x_{2} > x_{1} ，$ ，则y₂y₁；
对于函数y=-x+3，若x₂x₁ ，则 $y_{2} < y_{1}$

查看解析
5、把一张顶角为 $3 6^{\circ}$ 的等腰三角形纸片剪两刀，分成三张小纸片，使每张小纸片都是等腰三角形。你能办到吗?请画示意图说明剪法。

查看解析
6、风力发电机风轮的三个叶片的长度相等，每两个叶片(中心线)所成的角为120°。如果用线段把每两个叶片的外端连结起来，那么所得的三角形是等边三角形吗?请说明理由。

查看解析
7、如图，BD是等腰三角形ABC的底边AC上的高线，DE∥BC，交AB于点E。判断△BDE是不是等腰三角形，并证明你的判断。

查看解析
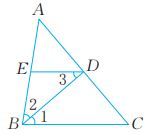
8、如图，在△ABC中，AB=AC，∠1=∠2。△ABD与△ACD全等吗?证明你的判断。

查看解析
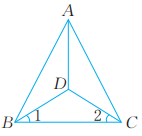
9、如图，AD平分△ABC的外角∠EAC，AD∥BC。△ABC是等腰三角形吗?证明你的判断。

查看解析
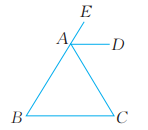
10、如图，上午8时，一艘船从A处出发，以15海里/时的速度向正北方向航行，9时45分到达B处。从A处测得灯塔C在北偏西 $2 6^{\circ}$ 方向，从B处测得灯塔C在北偏西52°方向。求B处到灯塔C的距离。

查看解析
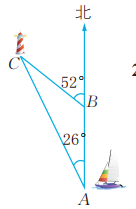
11、如图，有甲、乙两个三角形。甲三角形的内角分别为 $1 0^{\circ} ， 2 0^{\circ} ， 15 0^{\circ} ；$ 乙三角形的内角分别为 $8 0^{\circ} ， 2 5^{\circ} ， 7 5^{\circ} 。$ 。你能把三角形甲、乙分别分成两个等腰三角形吗?画一画，并标出各角的度数。
进一步探究：如果一个三角形能被分成两个等腰三角形，那么这个三角形的三个内角具有怎样的特征?

查看解析
12、已知：如图，在△ABC中，D，E分别是AB，AC上的点，DE∥BC，∠1=∠2。求证：△ABC是等腰三角形。

查看解析
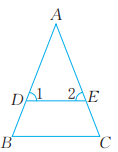
13、已知一个三角形的两个角的度数分别为43°，94°，这个三角形是不是等腰三角形?请说明理由。

查看解析
14、一次数学实践活动的内容是测量河宽，如图，即测量点A，B之间的距离。同学们想出了许多方法，其中小聪的方法是：从点A出发，沿着与直线AB成60°角的AC方向前进至C，在C处测得 $∠ C = 3 0^{\circ} 。$ 量出AC的长，它就是河的宽度(即点A，B之间的距离)。这个方法正确吗?请说明理由。

查看解析
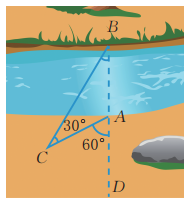
15、已知一条钢筋长100cm，把它折弯成长方形(或正方形)框，其一条边长记为x(cm)，围成的面积记为S(cm²)。

(1)、求S关于x的函数表达式和自变量x的取值范围。

(2)、分别求当x=20，25，28时，函数S的值。

查看解析
16、设y(cm²)表示周长比12cm小x(cm)的正方形面积，求：

(1)、y关于x的函数表达式和自变量x的取值范围。

(2)、当x=8时函数y的值。

查看解析
17、如果1cm³的钢的质量是7.8g，求一个立方体钢块的质量y(g)关于棱长x(cm)的函数表达式。

查看解析
18、一小汽车的油箱可装汽油50升，油箱中有汽油10升。现在再加汽油x(升)。已知每升汽油8.75元，求加油的费用y(元)关于x(升)的函数表达式，并求自变量x的取值范围。

查看解析
19、已知直角三角形两锐角的度数分别为x，y，则y与x的函数关系是。

查看解析
20、求下列函数自变量的取值范围(使函数式有意义)：

(1)、 $y = \frac{1}{x - 1} ；$

(2)、 $y = x - 1 。$

查看解析

上一页 261 262 263 264 265 下一页跳转

口罩型号	每只成本/元	每只售价/元
A	1	1.5
B	3	6