相关试卷
- 2017-2018学年人教版数学七年级下册同步训练： 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练：19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练： 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练： 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练： 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练：19.2.3《一次函数与方程、不等式》
-
1、如图，在5×5的方格纸中，每个小正方形的边长都为1，点A，B位于格点处.
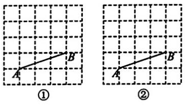(1)、分别在图①②中画出两个不全等的格点三角形ABC，使其内部(不含边)均有2个格点；(2)、任选一个你所画的格点三角形ABC，判断其是不是等腰三角形，并说明理由. -
2、高铁站候车厅的饮水机(图①)有温水、开水两个按钮，图②为其示意图.小明先接温水后再接开水，接满700mL的水杯，期间不计热损失.
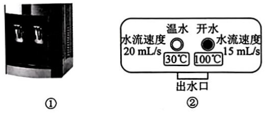
物理知识：开水和温水混合时会发生热传递，开水放出的热量等于温水吸收的热量，可转化为：开水体积×开水降低的温度=温水体积×温水升高的温度.
生活经验：饮水最佳温度是35~38 ℃(包括35 ℃与38 ℃)，这一温度最接近人体体温.
利用上述信息解决下列问题：
(1)、若小明先接温水26s，求他再接开水的时间.(2)、设小明接温水的时间为xs，接满水后水杯中水的温度为y℃.①若y=50，求x的值；
②求y关于x 的函数关系式，并写出达到最佳水温时x的取值范围.
-
3、为普及人工智能，某校组织七、八年级举行人工智能知识竞赛(满分10分，竞赛成绩均为整数，9分及以上为优秀).在两个年级中各随机抽取20名学生，相关数据整理如下：
七、八年级抽取学生的竞赛成绩统计表
平均数(分)
中位数(分)
众数(分)
七年级
7.4
a
7
八年级
7.4
8
b
八年级抽取学生的竞赛成绩统计表
成绩(分)
4
6
7
8
9
10
人数
2
4
3
6
3
2
根据以上信息，解答下列问题：
(1)、求a，b的值；(2)、已知该校七、八年级共有800名学生，估计本次竞赛成绩达到优秀的人数；(3)、你认为哪个年级学生对“人工智能”知识掌握的总体水平较好?请说明理由. -
4、已知：如图，在△ABC中，AD⊥BC于点D，E为AC上一点，BE与AD交于点F，且BF=AC，DF=DC.
(1)、求证：△BDF≌△ADC；(2)、若AC=5，DF=3，求AF的长. -
5、如图，在边长为1的小正方形组成的网格中建立直角坐标系，小正方形的顶点为格点，△ABC与△EFG的顶点都在格点上.
(1)、作△A1B1C1 ， 使△A1B1C1与△ABC关于原点O成中心对称；(2)、已知△ABC与△EFG关于点P成中心对称，请在图中画出点P的位置，并写出点P的坐标. -
6、先化简，再求值： 其中小明的解答过程如下，请指出其中错误步骤的序号，并写出正确的解答过程.
解：原式=
=a-2+4②
=a+2.③
当a=时，原式=
-
7、小南用一把可调节大小的活动扳手拧一枚正六边形螺丝帽(如图①)，其横截面示意图如图②所示.已知活动扳手的钳口AB∥CD，正六边形螺丝帽的两个顶点E，H分别在AB，CD上，EF=10mm，∠BEF=15°.
(1)、连结EH，求∠EHC的度数；(2)、在图②的基础上，调节活动扳手钳口大小，使得EF在直线AB上，HI在直线CD上(如图③)，请问AB和CD之间的距离减少了多少.(结果精确到1mm，参考数据： -
8、在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后按原路返回.设汽车从甲地出发x(h)时，汽车离甲地的路程为y(km)，y与x之间的函数关系如图所示.根据图象信息，解答下列问题：
(1)、这辆汽车的往、返速度是否相同?请说明理由；(2)、求当这辆汽车从甲地出发几小时时，离乙地的路程为60km. -
9、为了解A，B两款扫地机器人在一次充满电后运行的最长时间，有关人员分别随机调查了 A，B两款扫地机器人各10台，记录下它们运行的最长时间(单位：分)，并对数据进行整理、描述和分析(运行最长时间用x表示，共分为四组：不合格：x<90，合格：90≤x<100，良好：100≤x<110，优秀：x≥110).下面给出了部分信息：
10台 A款扫地机器人一次充满电后运行最长时间的数据分别是112，90，96，101，99，98，101，105，101，97.
10台B款扫地机器人一次充满电后运行最长时间属于良好的数据分别是101，102，104，100，103，102.
两款扫地机器人运行最长时间统计表
平均数
(分)
中位数
(分)
众数
(分)
方差
(分2 )
A
100
100
a
30.2
B
100
b
102
32.8
根据以上信息，解答下列问题：
(1)、求上述图表中a，b，m的值；(2)、根据题中的信息和数据，你认为哪款扫地机器人运行性能更好?请说明理由(写出一条理由即可). -
10、按下列要求完成作图：①仅用无刻度直尺，且不能用直尺中的直角；②保留作图痕迹).
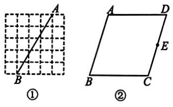(1)、如图①是5×5的正方形网格，点A，B均在格点上，作线段AB的中点G；(2)、如图②，在□ABCD中，E为CD的中点，作边BC的中点F. -
11、观察以下等式：
第1个等式：2×2=2+2，
第2个等式：
第3个等式：
第4个等式：
………
按照以上规律，解决下列问题：
(1)、请直接写出第6个等式；(2)、写出你猜想的第n个等式，并证明. -
12、如图，在平面直角坐标系中，已知A（0，a），B（b，0），其中a，b满足|a-2|+（b-3）2=0．
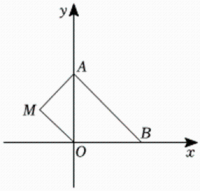(1)、求a，b的值；(2)、如果在第二象限内有一点M（m，1），请用含m的式子表示四边形ABOM的面积． -
13、某服装店用6200元购进A，B两种新式服装，按标价售出后可获得毛利润3300元．这两种服装的进价、标价见下表．
单价（元/件）
A种
B种
进价
200
320
标价
300
500
(1)、这两种服装各购进多少件？(2)、如果A种服装按标价的8折售出、B种服装按标价的7.5折售出，那么这批服装全售完后，服装店比按标价售出收入减少多少元？ -
14、为了解“双减”落实情况，某初中学校随机调查了部分学生每天书面作业平均完成时间，并将调查结果绘制成不完整的频数分布表和频数分布直方图（如图），根据图表信息解答下列问题：
每天书面作业平均完成时间/h
频数
百分比
0＜t≤0.5
15
0.5＜t≤1
35
35%
1＜t≤1.5
40%
1.5＜t≤2
10
n
合计
m
100%
(1)、m= ，n= ．(2)、补全频数分布直方图．(3)、教育部规定初中生每天书面作业完成时间平均不超过90min，该校共有1500名学生，试估计该校学生每天书面作业平均完成时间超出规定的人数． -
15、已知△AOB在平面直角坐标系中的位置如图所示．
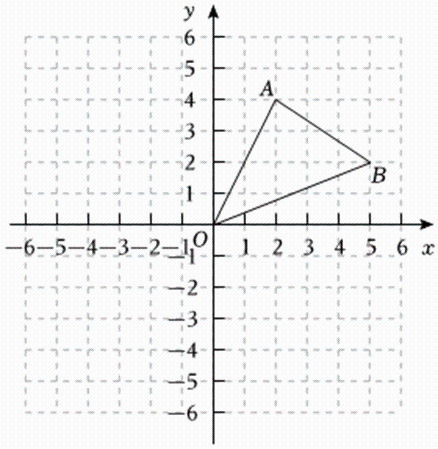(1)、写出A、B两点的坐标；(2)、将△AOB向左平移3个单位长度，向下平移4个单位长度，得到△A1O1B1 ， 画出△A1O1B1 ， 并写出A1 ， B1 ， O1的坐标． -
16、如果关于x的不等式1≤3x-8＜m-1有4个整数解，求m的取值范围．
-
17、计算：
-
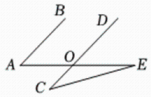
18、如图，AB∥CD，∠C=18°，∠C=∠E，则∠A的度数是 ．
-
19、如图，直线AB与直线CD相交于点O，OE⊥OF，且OA平分∠COE，若∠DOE=50°，则∠BOF的度数为 ．
-
20、围棋，起源于中国，古代称为“弈”，是棋类鼻祖，距今已有4000多年的历史，如图是某围棋棋盘的局部，若棋盘是由边长均为1的小正方形组成的，棋盘上A、B两颗棋子的坐标分别为A（-2，4），B（1，2），则棋子D的坐标为 ．
