相关试卷

1、有三个纸箱，一个箱内装有橘子，一个箱内装有苹果，一个箱内混装了一些橘子和苹果.三个箱子外面分别贴有“橘子”“苹果”“混合水果”的标签，可是工作人员不慎将所有标签都贴错了.请你只检查一个箱子即确定各箱子内的水果品种.

查看解析
2、如图，直线a， b被直线 OA， OB所截. 已知. $∠ 1 = 12 0^{\circ}, ∠ 2 = 6 0^{\circ}, ∠ 3 = 7 0^{\circ},$ 你还能求出哪些角的度数?

查看解析
3、如图，直线a，b被直线c所截.

(1)、如果a∥b，你能得到哪些角之间的等量关系?

(2)、写出能够证明a∥b的条件(能写几个就写几个).

查看解析
4、小丽发现： $\sqrt{2} + \sqrt{3}$ 是无理数， $\sqrt{3} + \sqrt{5}$ 是无理数， $\sqrt{5} + \sqrt{7}$ 是无理数.于是她猜想：两个无理数的和一定还是无理数.你认为她的猜想正确吗?为什么?

查看解析
5、小华将n=0，1，2分别代入代数式 $n^{4} - 6 n^{3} + 11 n^{2} - 6 n,$ 结果发现这个代数式的值都是0.于是他猜想：对于所有的自然数，代数式 $n^{4} - 6 n^{3} + 11 n^{2} - 6 n$ 的值都是0.你认为小华的猜想正确吗?为什么?

查看解析
6、已知：如图， AB∥CD， PM和QN分别是 $∠ B P E 和 ∠ D Q E$ 内的两条射线，且∠BPM=∠DQN.
求证： PM∥QN.

查看解析
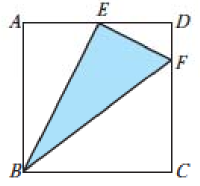
7、将正方形的四个顶点用线段连接，什么样的连法最短?研究发现，并非对角线最短，而是如图所示的连法最短(即用线段 AE，DE，EF，BF，CF把四个顶点连接起来 ).已知图中. $∠ D A E = ∠ A D E = 3 0^{\circ}, ∠ A E F = ∠ B F E = 12 0^{\circ},$ 请证明 $A B | | E F$ .

查看解析
8、已知：如图，点O在直线AB上，射线OC平分∠AOD，且OC⊥OE.
求证： ∠DOE=∠BOE.

查看解析
9、如果只给你一根长绳子，那么你如何利用它得到一个直角?

查看解析

10、美国哥伦比亚大学收藏有一块古巴比伦时代的泥板，其中有4列15行数字.经研究，这块泥板第二列、第三列的数字实际上相当于下表第二列、第三列的数字，而且每一行的第二列数字、第三列数字与下表中同一行的第一列数字都存在着同一种关系.你知道这些数字间的关系吗?借助计算器进行探索.

第一列	第二列	第三列
120	119	169
3 456	3 367	4 825
4 800	4 601	6 649
13 500	12 709	18 541
72	65	97
360	319	481
2 700	2 291	3 541
960	799	1 249
600	481	769
6 480	4961	8 161
60	45	75
2 400	1679	2 929
240	161	289
2 700	1771	3 229
90	56	106

查看解析

11、如图，哪些三角形是直角三角形，哪些不是?说说你的理由.

查看解析
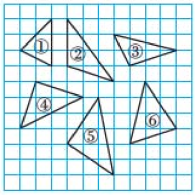
12、如果将直角三角形的三条边长同时扩大相同的倍数，那么得到的三角形还是直角三角形吗?你还能提出什么问题?

查看解析
13、如果三条线段a，b，c 满足 $a^{2} = c^{2} - b^{2},$ 那么这三条线段组成的三角形是直角三角形吗?为什么?

查看解析
14、如图，在正方形 ABCD 中， AB=4， AE=2，DF=1，图中有几个直角三角形?你是如何判断的?

查看解析
15、下列几组数能否作为直角三角形的三边长?说说你的理由.

(1)、9， 12， 15；

(2)、12， 18， 22；

(3)、12， 35， 36；

(4)、15， 36， 39.

查看解析
16、一个零件的形状如图1所示，按规定这个零件中∠A和 $∠ D B C$ 都应为直角.工人师傅量得这个零件各边尺寸如图2所示(单位：cm)，这个零件符合要求吗?

查看解析
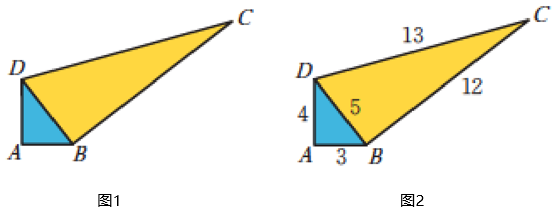
17、改革开放后我国发生了翻天覆地的变化，你认为可以从哪些角度反映改革开放取得的成就?小组合作，选择其中一个或几个角度开展统计活动，撰写活动报告.

查看解析
18、某银行网点为了解客户的等待时间(从进入银行网点到开始办理业务的时间间隔)，随机调查了20名客户，所得数据(单位：min)如下：
23 30 35 42 37 24 21 1 14 12
34 22 13 34 8 22 31 24 17 33
根据以上数据，设法用多种方式描述该银行网点顾客的等待情况，并给该银行网点提一条改进建议.

查看解析
19、利用统计图或统计量获取数据信息，你有哪些经验?请在班级内分享.

查看解析
20、2024年，盛李豪在与队友黄雨婷合作获得巴黎奥运会及中国代表团的首枚金牌后，又以252.2环的成绩获得男子10米气步枪金牌并打破奥运会记录.在决赛阶段他和瑞典选手林德格伦各轮次的成绩(单位：环)见下表：
选手
轮次
总计
1
2
3
4
5
6
7
8
9
盛李豪
53.4
52.4
20.7
21.7
21.6
20.4
20.3
20.6
21.1
252.2
林德格伦
52.5
52.1
21.0
20.8
21.2
21.1
20.6
21.2
20.9
251.4
试评价两位运动员在决赛中的表现.（前2轮各打5枪，第3~9轮每轮打2枪.）

查看解析

上一页 470 471 472 473 474 下一页跳转

选手	轮次									总计
选手	1	2	3	4	5	6	7	8	9	总计
盛李豪	53.4	52.4	20.7	21.7	21.6	20.4	20.3	20.6	21.1	252.2
林德格伦	52.5	52.1	21.0	20.8	21.2	21.1	20.6	21.2	20.9	251.4