相关试卷

1、一天下午，某出租车以希望小学为出发点在东西方向营运，行车情况依先后次序记录如下（向东为正方向，单位： $km$ ）：
$+ 9$ ， $+ 3$ ， $- 5$ ， $+ 4$ ， $- 8$ ， $+ 16$ ， $- 3$ ， $- 12$ ．

(1)、将最后一名乘客送到目的地，出租车在出发点位置的东边还是西边？离出发点多远？

(2)、若出租车在行驶过程中，每千米耗油 $0.08$ 升，出租车一下午共耗油多少升？

查看解析
2、小明同学在学习完有理数的运算后，对运算产生了浓厚的兴趣，她借助有理数的运算，定义了一种新运算“ $\oplus$ ”，运算规则为： $a \oplus b = a \times b + 2$ ．如： $2 \oplus 6 = 2 \times 6 + 2$

(1)、求 $2 \oplus 4$ 的值；

(2)、求 $(- 3) \oplus (2 \oplus \frac{1}{2})$ 的值．

查看解析
3、已知 $a 、 b$ 互为相反数， $x 、 y$ 互为倒数， $m$ 是最大的负整数，求 $6 (a + b) + |m| - 3 x y$ 的值．

查看解析
4、在数轴上表示下列各数，并用“<”把这些数连接起来．
$- 3$ ；3.5； $- (- 2 \frac{1}{2})$ ； $|- 1|$ ．

查看解析
5、计算：

(1)、 $6 + (- 4) - 2 + 3$

(2)、 $(\frac{1}{2} - \frac{2}{3} + \frac{5}{6}) \times (- 24)$

查看解析
6、如果电梯上升5米，记作+5米，那么下降8米可记作米．

查看解析
7、根据流程图中的运算程序，当输入数据 $x = - 1$ 时，输出结果 $y$ 为（）

A、9 B、 $- 9$ C、25 D、 $- 25$

查看解析
8、如图，将刻度尺放在数轴上，让 $3 cm$ 和 $5 cm$ 刻度线分别与数轴上表示2和4的两点重合对齐，则数轴上与 $0 cm$ 刻度线对齐的点表示的数为（）

A、 $- 1$ B、0 C、1 D、2

查看解析
9、一个两位数，十位上的数字是 $b$ ，个位上的数字是 $a$ ，这个两位数是（）

A、 $a + b$ B、 $10 (a + b)$ C、 $10 a + b$ D、 $10 b + a$

查看解析
10、在 $3.14$ ， 2024， $- \frac{22}{7}$ ， $π$ 四个数中有理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看解析
11、南岸区是一个充满生机和活力的市区，它古老而又年轻，区域内人口约为1200000人．则1200000用科学记数法可表示为（　　）

A、 $120 \times 10^{4}$ B、 $12 \times 10^{5}$ C、 $1.2 \times 10^{6}$ D、 $0.12 \times 10^{7}$

查看解析
12、如图，在直角三角形ABC中，∠C=90°，∠B=60°，AB=8cm，E、F分别为边AC、AB的中点．
（1）求∠A的度数；
（2）求EF和AE的长．

查看解析
13、已知直线 $y_{1} = m x + 3 n - 1$ 与直线 $y_{2} = (m - 1) x - 2 n + 2$ ．

(1)、如果 $m = - 1, n = 1$ ，当x取何值时， $y_{1} > y_{2}$ ？

(2)、如果两条直线相交于点A，A点的横坐标x满足 $- 1 < x < 13$ ，求整数n的值．

查看解析
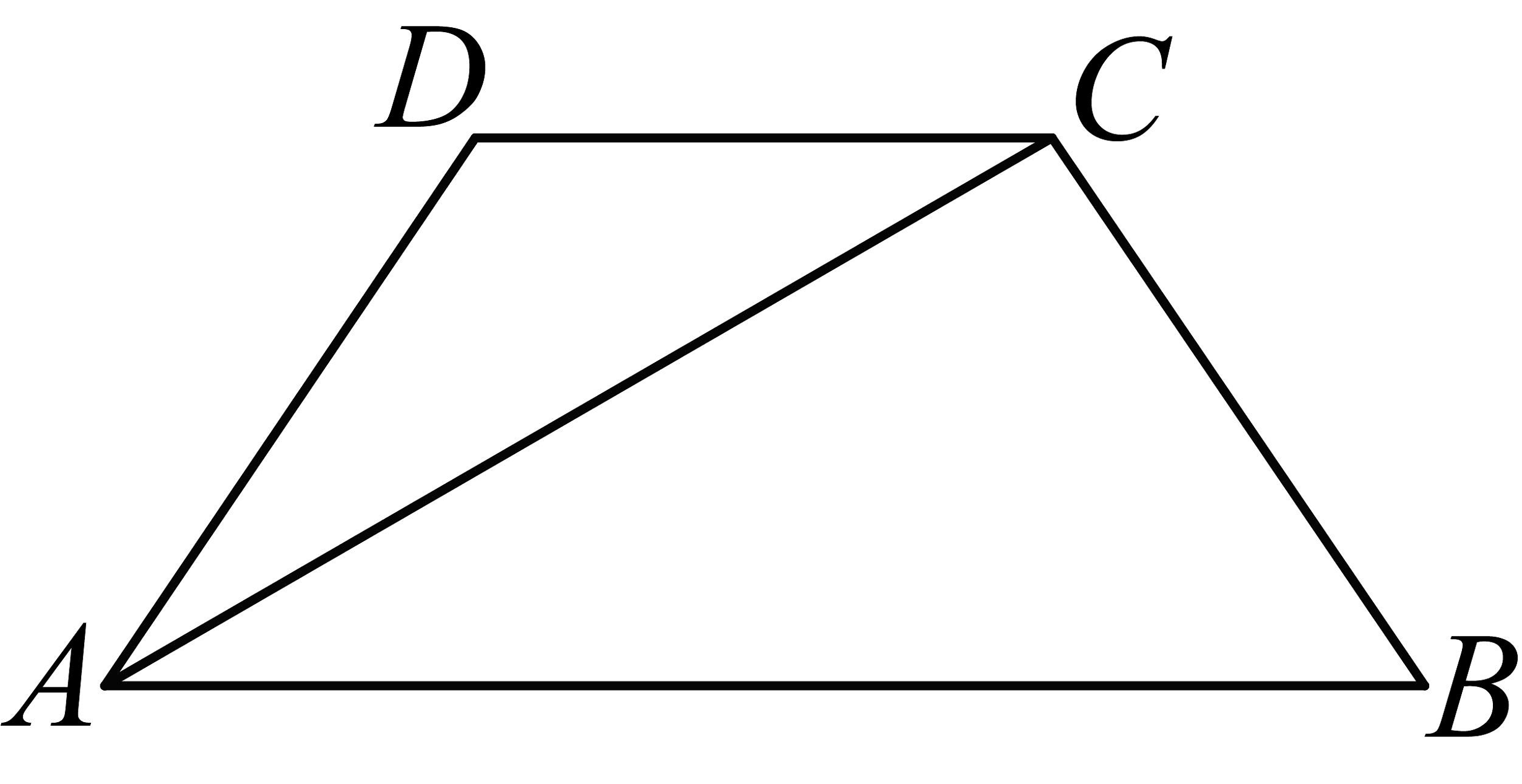
14、如图，在ABCD中，AB∥CD，AD＝BC，∠B＝60°，AC平分∠DAB．
(1)求∠ACB的度数；
(2)如果AD＝1，请直接写出向量 $\overset{⃑}{D C}$ 和向量 $\overset{⃑}{B C} + \overset{⃑}{C D} + \overset{⃑}{D A}$ 的模．

查看解析
15、在三角形 $A B C$ 中，点 $D, E, F$ 分别是 $B C, A B, A C$ 的中点， $A H ⊥ B C$ 于点 $H$ ，若 $∠ D E F = 50^{\circ}$ ，则 $∠ C F H =$ .

查看解析
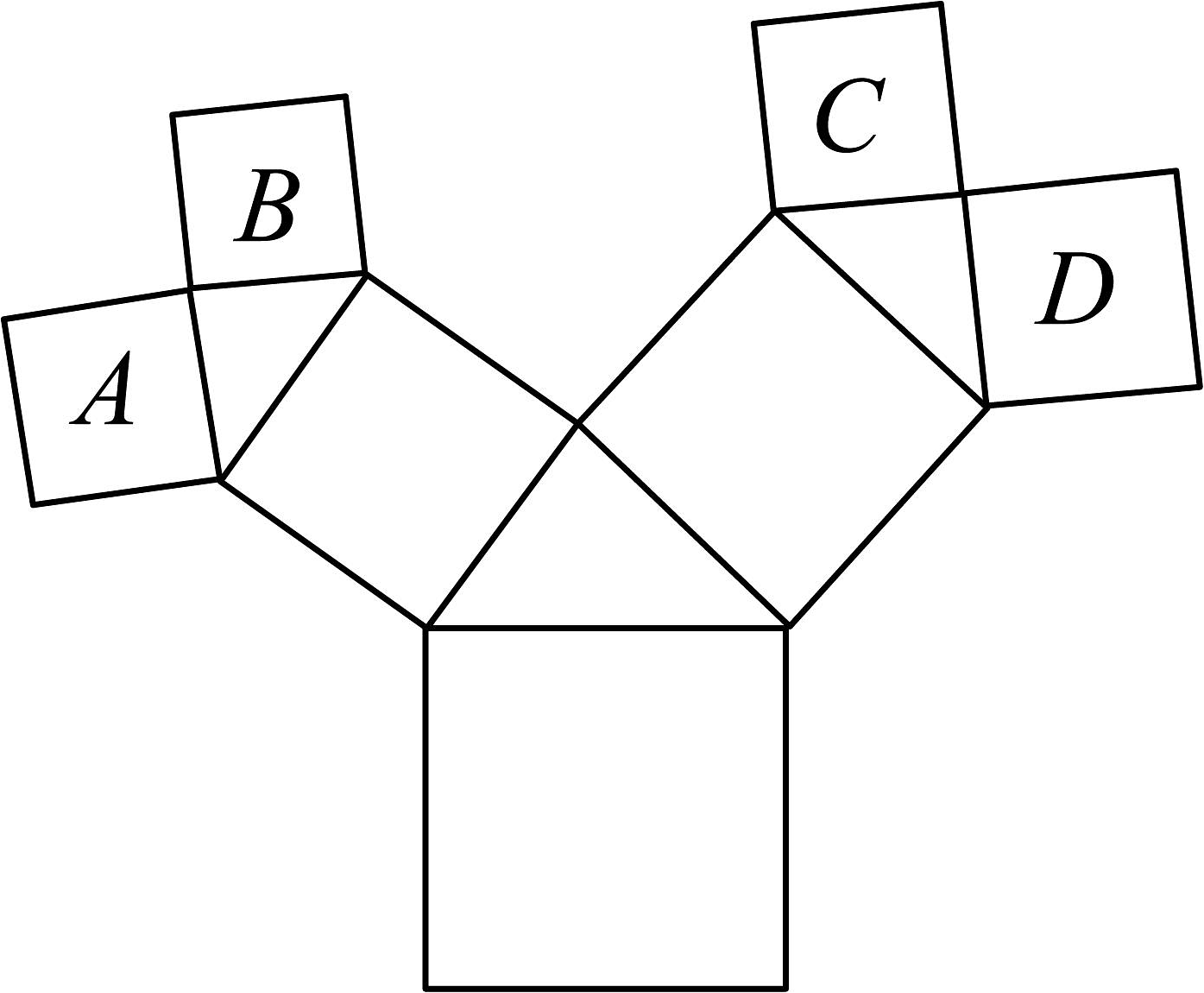
16、如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的面积为49，则正方形A、B、C、D的面积之和为．

查看解析
17、计算：
（1） $\sqrt{8} - | \sqrt{2} - 2 | + \sqrt{{(- 2)}^{2}}$ ；
（2） $\frac{3 - \sqrt{3}}{\sqrt{3}} + (3 + \sqrt{3}) (3 - \sqrt{3})$

查看解析
18、某校团委积极响应南充市“书香天府万卷南充”全民阅读活动，号召全校学生积极捐献图书共建“书香校园”．八（1）班40名同学都捐献了图书，全班40名同学共捐图书320册．班长统计了全班捐书情况如表：
册数
4
5
6
7
8
50
人数
6
8
15
2
（1）分别求出该班级捐献7册图书和8册图书的人数；
（2）请算出捐书册数的平均数、中位数和众数，并判断其中哪些统计量不能反映该班同学捐书册数的一般状况，说明理由

查看解析
19、一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：
点 $P (x_{0}, y_{0})$ 到直线 $A x + B y + C = 0$ 的距离 $(d)$ 公式是： $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$
如：求：点 $P (1,1)$ 到直线 $2 x + 6 y - 9 = 0$ 的距离．
解：由点到直线的距离公式，得 $d = \frac{| 2 \times 1 + 6 \times 1 - 9 |}{\sqrt{2^{2} + 6^{2}}} = \frac{1}{\sqrt{40}} = \frac{\sqrt{10}}{20}$
根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．
则两条平行线 $l_{1}$ ： $2 x + 3 y = 8$ 和 $l_{2}$ ： $2 x + 3 y + 18 = 0$ 间的距离是．

查看解析
20、若函数 $y = \frac{1}{x - 1}$ 有意义，则（）

A、 $x > 1$ B、 $x < 1$ C、 $x = 1$ D、 $x \neq 1$

查看解析

上一页 413 414 415 416 417 下一页跳转

册数	4	5	6	7	8	50
人数	6	8	15			2