相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
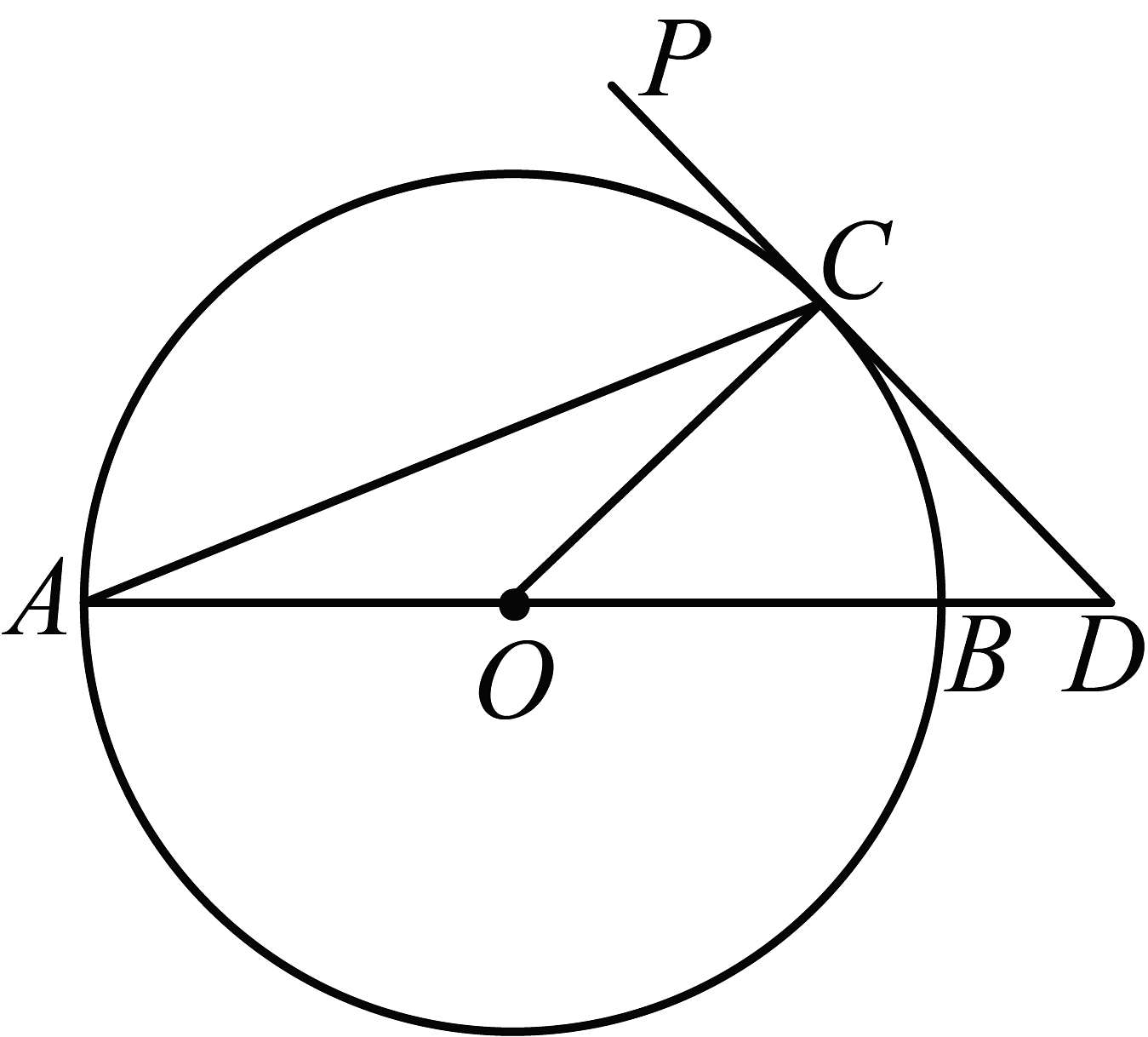
(1)求∠D的度数;
(2)若CD=2,求BD的长.
-
2、如图,A,P,B,C是直径为8的上的四点,且满足 .
 (1)、求证:是等边三角形;(2)、求圆心O到的距离 .
(1)、求证:是等边三角形;(2)、求圆心O到的距离 . -
3、如图,PA、PB是⊙O的两条切线,切点分别为A、B,若直径AC=12cm,∠P=60°.求弦AB的长.
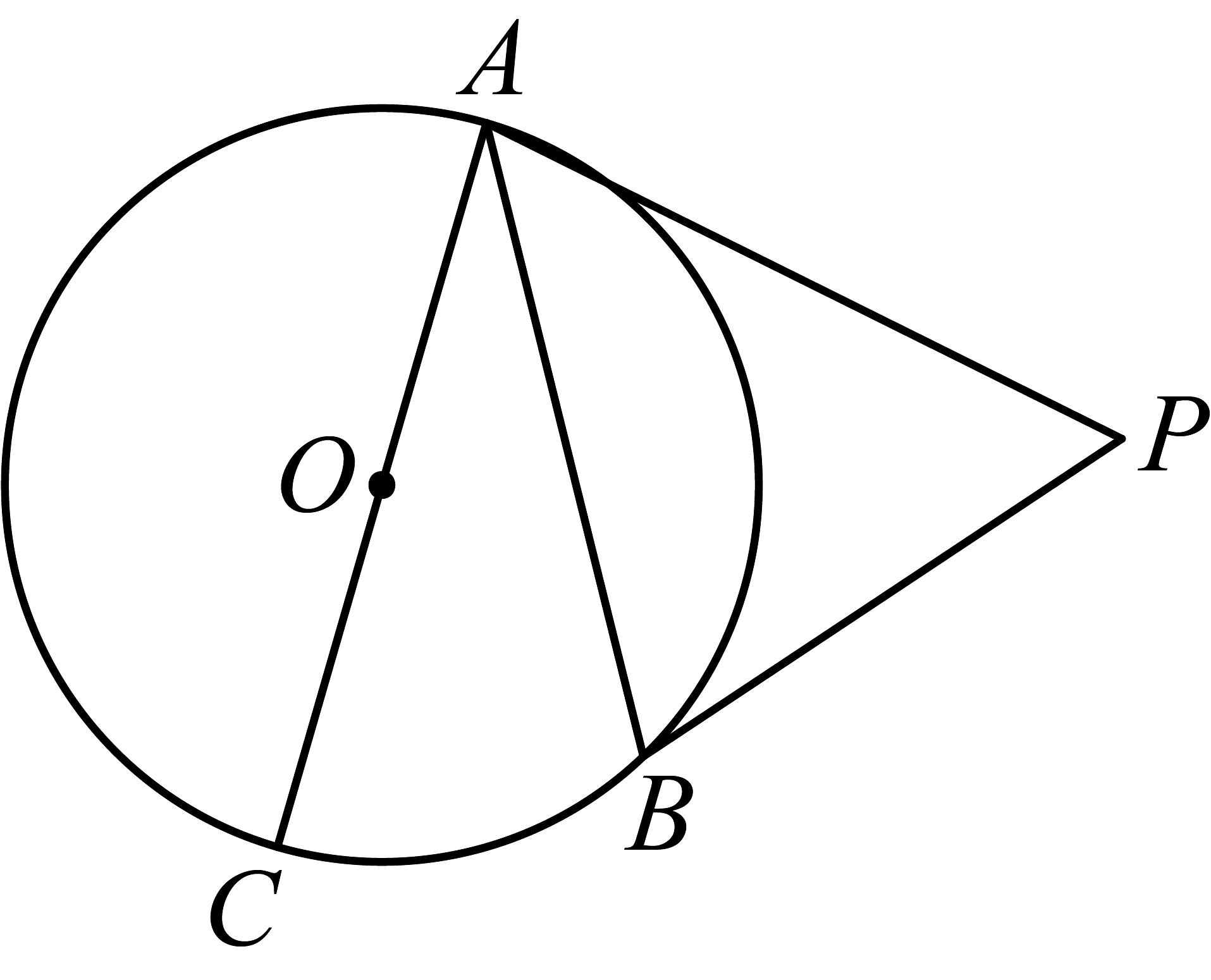
-
4、如图,某公园的石拱桥的桥拱是圆弧形(弓形),其跨度AB=24m,拱的半径R=13m,求拱高CD.
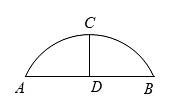
-
5、将二次函数的图象向上平移a个单位长度,当抛物线与两坐标轴有且只有2个公共点时,a的值为 .
-
6、如图,为美化校园环境,某校计划在一块长为60m,宽为40m的矩形空地上,修建一个矩形花圃,并将花圃四周余下的空地建成同样宽的通道.若通道所占面积是整个矩形空地面积的 , 则此时通道的宽为 .

-
7、如图,在中,弦与交于点M, , 则的度数是 .
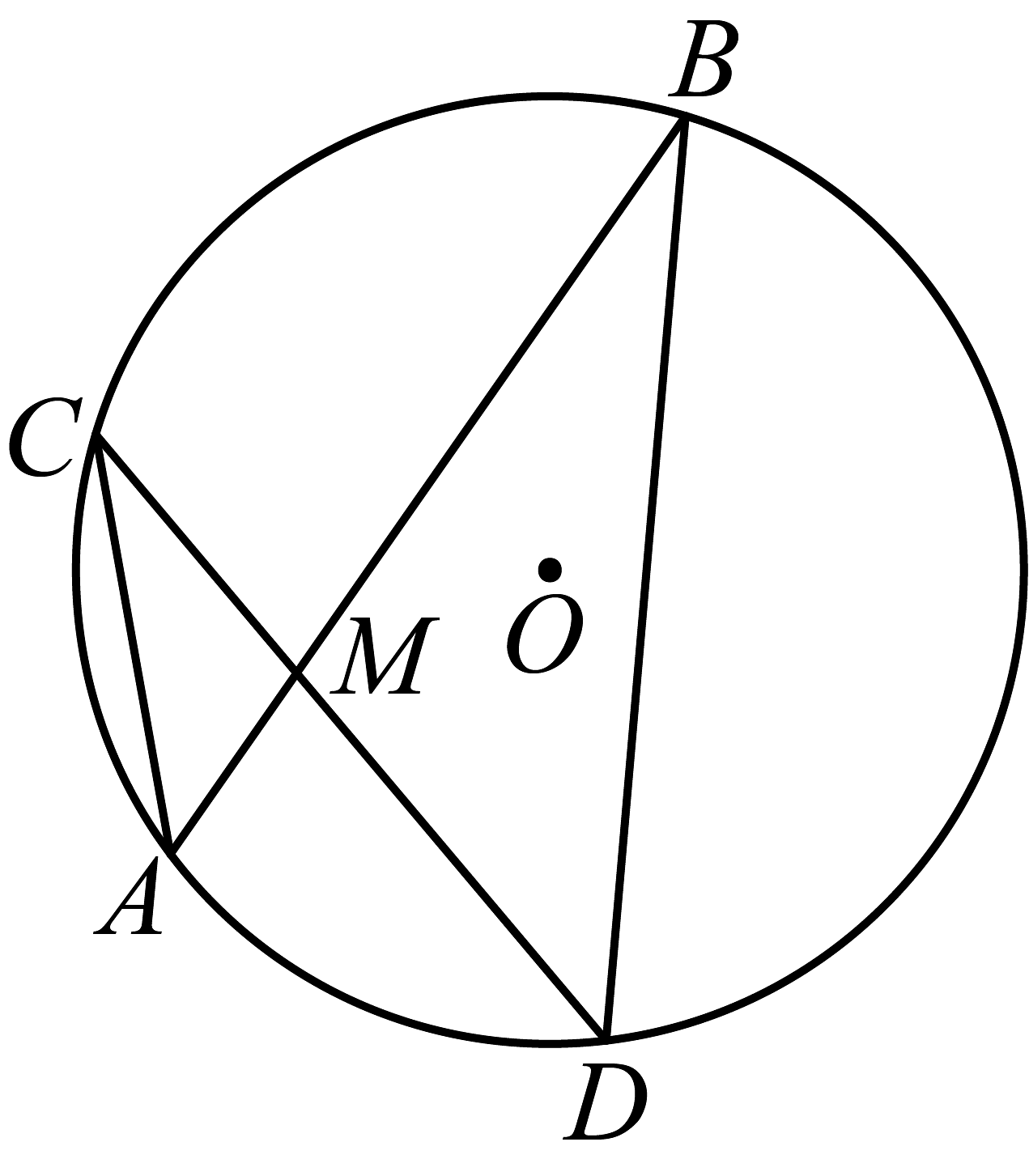
-
8、如图,在中,已知 , 将绕点A按逆时针方向旋转后得到 , 则图中阴影部分的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、如图,在平面直角坐标系中,点A在x轴负半轴上,点B在y轴正半轴上,经过四点, , , 则圆心点D的坐标是( )
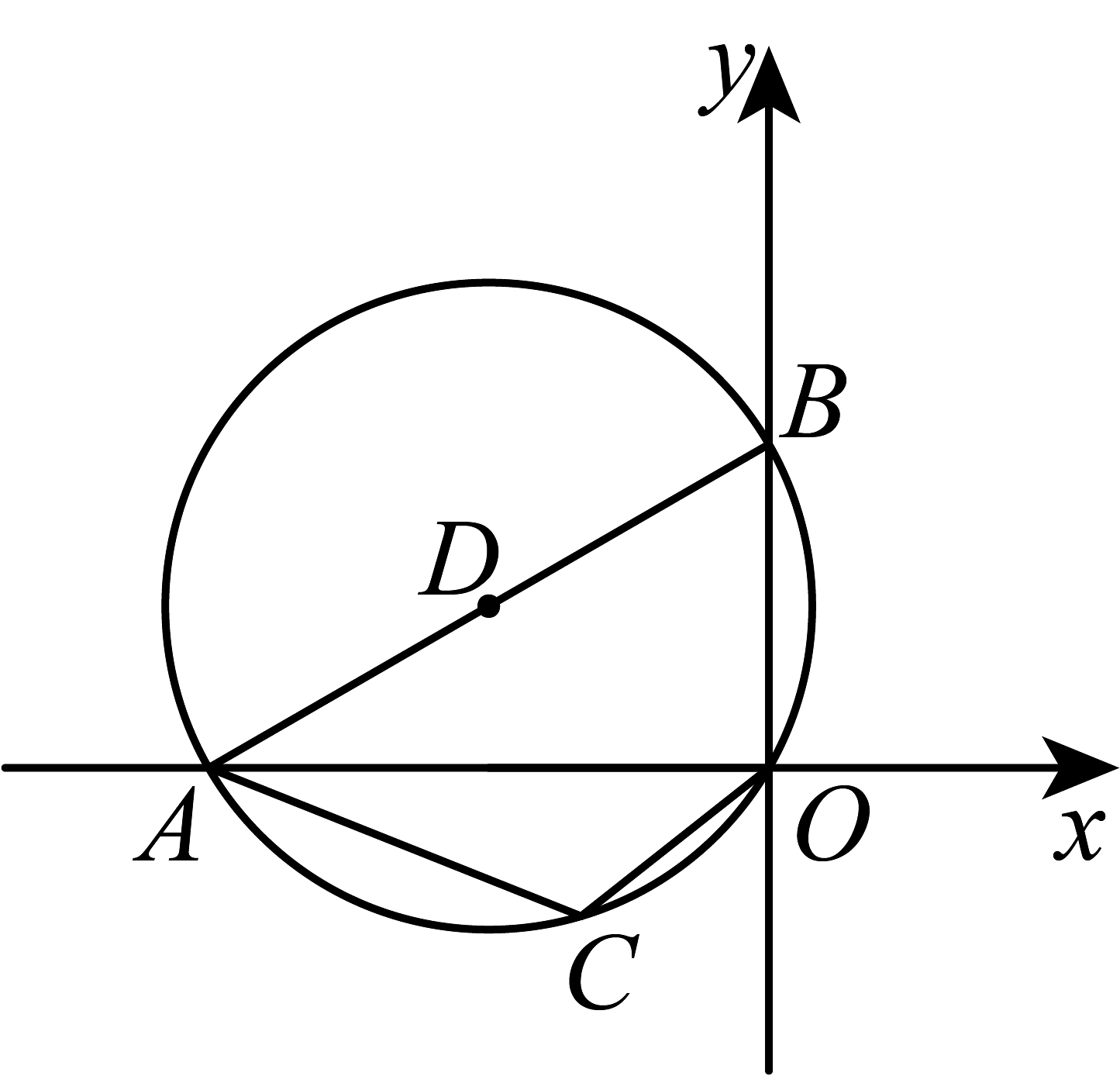 A、 B、 C、 D、
A、 B、 C、 D、 -
10、如图所示,矩形纸片中, , 把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则的长为( )
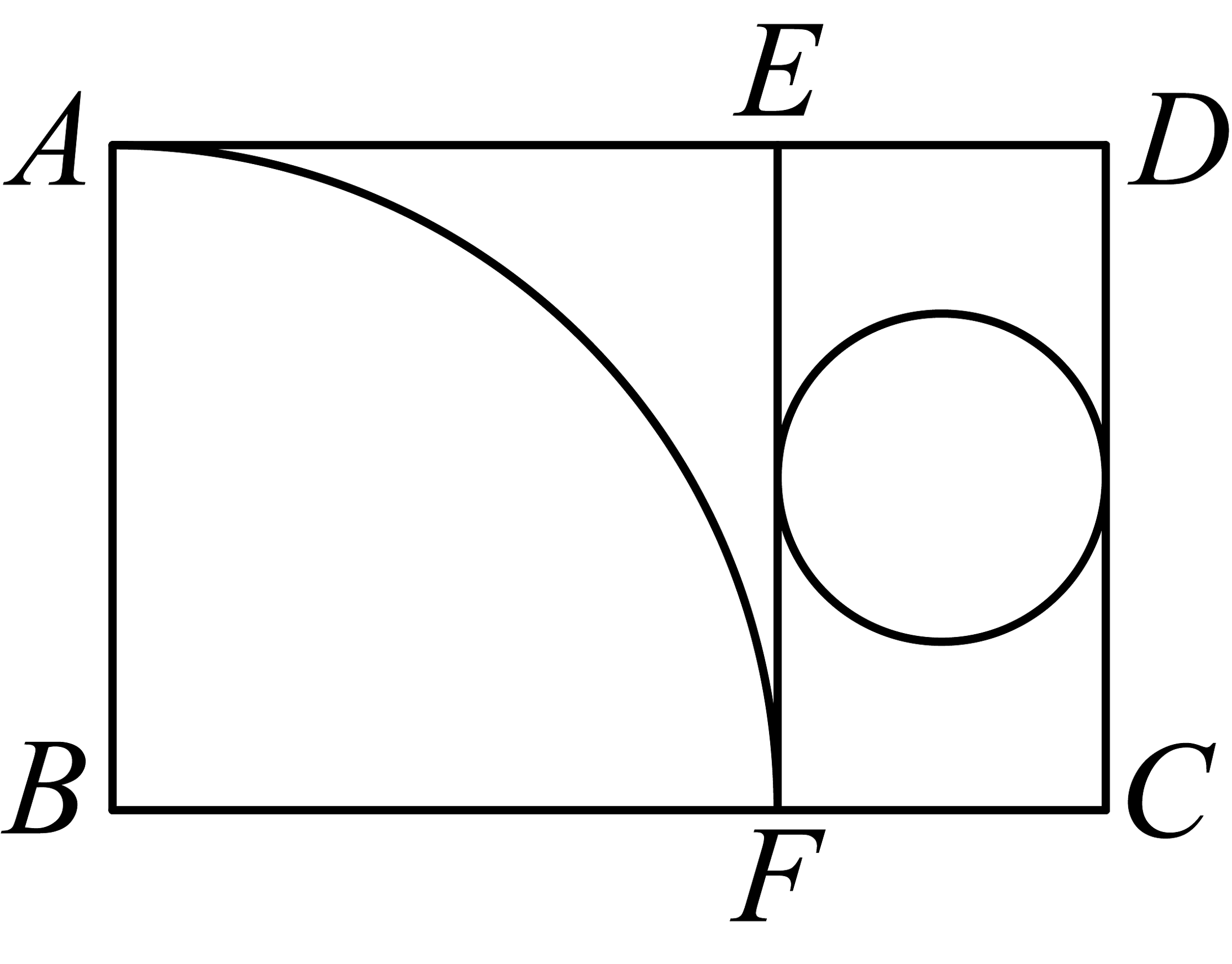 A、 B、 C、 D、
A、 B、 C、 D、 -
11、已知圆的内接正三角形的边心距是1,则这个三角形的边长是( )A、 B、 C、2 D、
-
12、如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
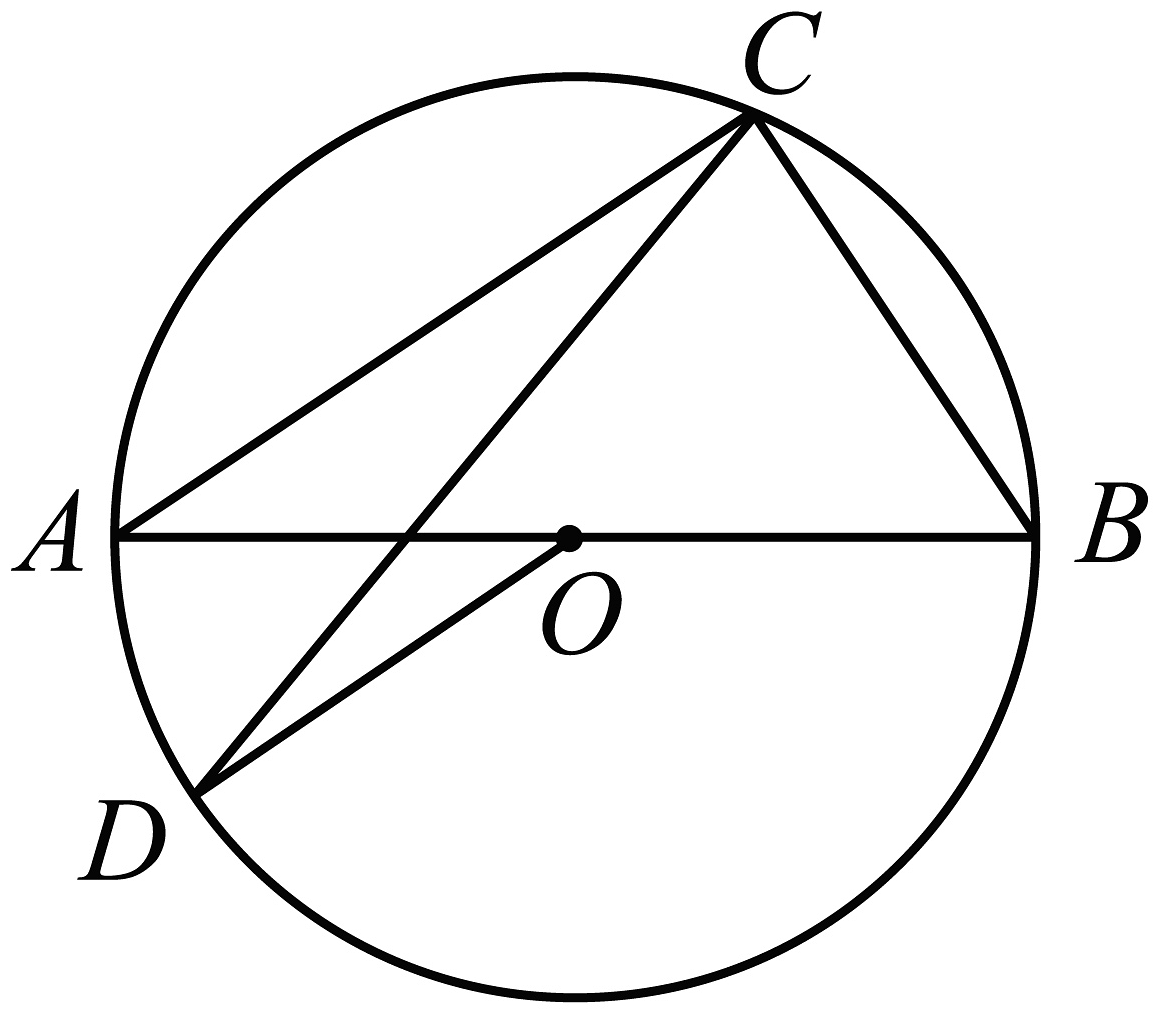 A、20° B、30° C、40° D、70°
A、20° B、30° C、40° D、70° -
13、如图,在中,半径垂直于弦 , 垂足为C, , 则等于( )
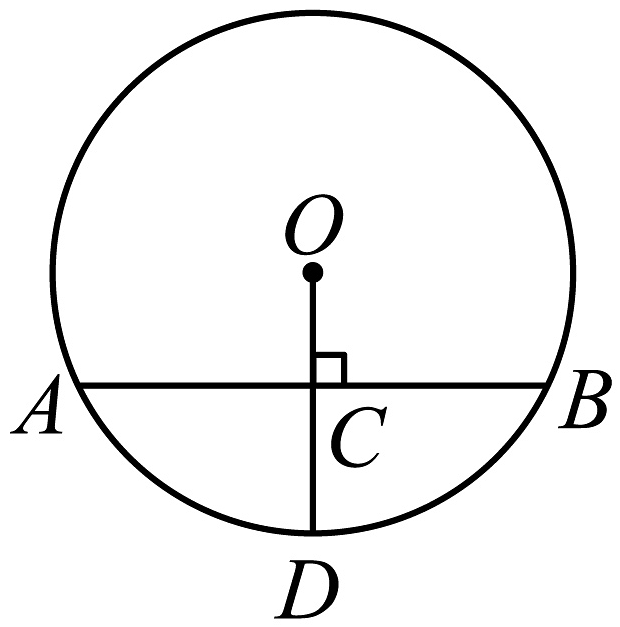 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图,在△ABC中,AB=BC=2,以AB为直径的⊙O与BC相切于点B,则AC的长为( )
 A、 B、 C、2 D、2
A、 B、 C、2 D、2 -
15、如图,A,B,C是上的三点,且 , 则的度数是( )
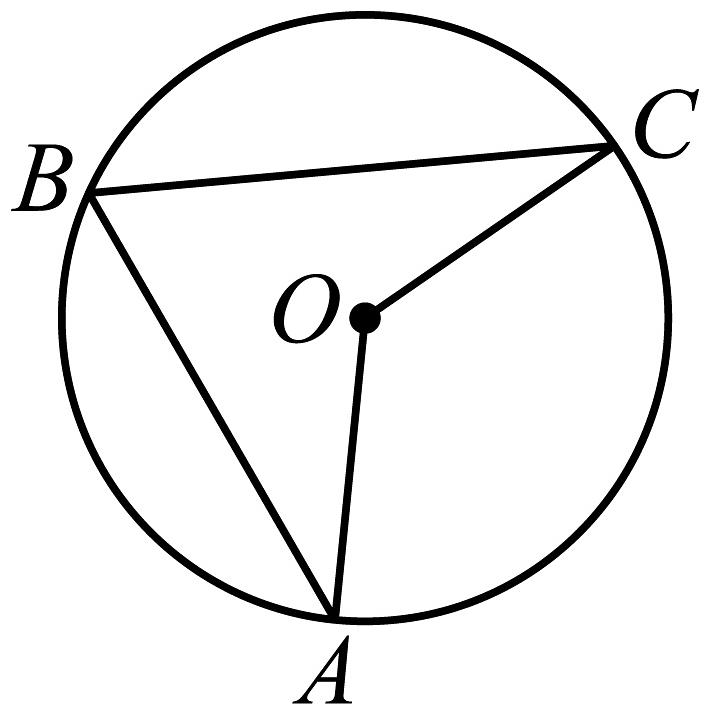 A、 B、 C、 D、或
A、 B、 C、 D、或 -
16、如图,与关于成中心对称,下列结论中不成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、将二次函数的图象向右平移4个单位长度,再向上平移5个单位长度后,所得图象对应的函数解析式是( )A、 B、 C、 D、
-
18、下列方程是一元二次方程的是( )A、 B、 C、 D、
-
19、综合与实践:【问题情境】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系.数学活动课上,王老师出示了一个问题:点、在数轴上分别表示有理数、 , 则在数轴上、两点之间的距离为 . 如:表示为3与1两数在数轴上所对应的两点之间的距离;表示为3与两数在数轴上所对应的两点之间的距离.

利用数形结合思想回答下列问题:
(1)数轴上表示2和7两点之间的距离是______;数轴上表示2和的两点之间的距离是______;
【解决问题】:
(2)数轴上表示和的两点之间的距离表示为______.
(3)试用数轴探究:当时的值为______.
【实践探究】利用绝对值的几何意义,结合数轴,探究:
(4)利用数轴求出的最小值为______,并写出此时可取的整数值为______.
-
20、【阅读材料】“整体思想”是中学数学解题中的一种重要的思想方法,运用“整体思想”的方法在求代数值中非常重要,有这样一道题:
代数式:的值为9,则代数式的值为.
小明在做作业时采用的方法如下:
由题意得 , 则有 .
所以
.
所以代数式的值为9.
【方法运用】
(1)、若 , 则______.(2)、若代数式的值为15,求代数式的值.