相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、把下列多项式分解因式:(1)、;(2)、 .
-
2、已知 , 则的值为 .
-
3、小明是一个电脑爱好者,他设计了一个程序,其流程图如下,当输入的值是64时,输出的值是 .

-
4、若 , 则代数式的值是 .
-
5、观察下列算式: , , , …,它具有一定的规律性,若把第个算式的结果记为 , 则的值是( )A、 B、 C、 D、
-
6、如果是一个完全平方式,那么的值为( )A、8 B、 C、或8 D、或5
-
7、若关于的代数式的展开式不含的二次项,则的值为( )A、2 B、 C、 D、
-
8、已知 , , 则的值等于( )A、 B、 C、1 D、2
-
9、观察下图,用等式表示图中图形面积的运算正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、下列计算正确的是( )A、 B、 C、 D、
-
11、观察下列各式:
;;;;….
(1)、用你发现的规律填写下列式子的结果:;(2)、用你发现的规律计算: . -
12、用“”定义新运算:对于任意有理数 , 当时,都有;当时,都有 .(1)、求的值;(2)、定义一种运算,就要研究它的运算律:
①求和的值;
②这个计算结果说明了这个运算满足 律.
-
13、有理数在数轴上的位置如图所示:
 (1)、请在数轴上标出;(2)、比较的大小(用“”将它们连接起来).
(1)、请在数轴上标出;(2)、比较的大小(用“”将它们连接起来). -
14、计算:(1)、;(2)、;(3)、 .
-
15、如图所示的是一个简单的数值运算程序.当输入的值为4时,输出的值为 .

-
16、绝对值大于3且小于5的所有整数的和是 .
-
17、下列用四舍五入法分别取近似数,其中错误的是( )A、0.1(精确到0.1) B、0.05(精确到百分位) C、8.12亿(精确到百分位) D、(精确到十万位)
-
18、下列各式中计算正确的是( )A、 B、 C、 D、
-
19、有理数a,b在数轴上的对应点的位置如图所示,在中,正数有( )
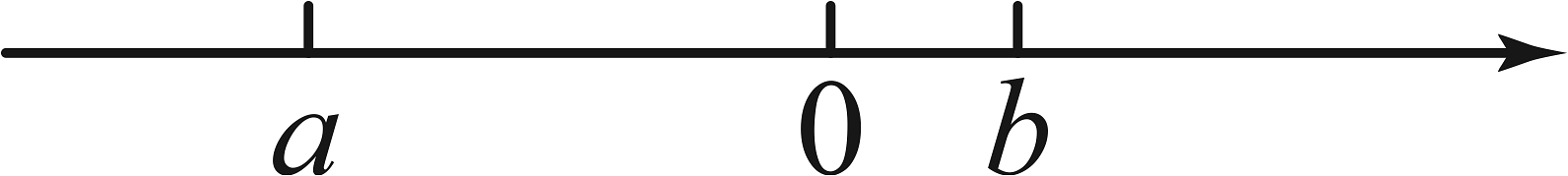 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
20、下列式子一定成立的是( )A、 B、 C、 D、