相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、使式子有意义的条件是 .
-
2、关于的分式方程有增根,则它的增根是( )A、 B、 C、或 D、
-
3、计算的结果是( )A、1 B、 C、 D、
-
4、下列变形不正确的是( )A、 B、 C、 D、
-
5、下列各命题中,假命题的个数为( )
①相等的角形是对顶角;②两个角相等的三角形是等边三角形;③三角形的内角和是;④两直线平行,内错角相等.
A、1 B、2 C、3 D、4 -
6、如图1,在中, , , 点D在边上运动,沿着折叠得到 , 直线与直线相交于点.
 (1)、如图2,若 , , 求的长度;(2)、当为等腰直角三角形时,求的值;(3)、若 , 为钝角三角形,直接写出长度的取值范围.
(1)、如图2,若 , , 求的长度;(2)、当为等腰直角三角形时,求的值;(3)、若 , 为钝角三角形,直接写出长度的取值范围. -
7、某校八年级同学测量池塘两端A,B的距离,测量方案如下表:
课题
测量池塘两端A,B的距离
测量工具
皮尺,标杆
测量方案示意图

测量步骤及数据
(1)利用标杆确定A,M,F在同一直线上,量得 , 然后找到了点N,且 , ;
(2)测得 , 再在的延长线方向确定点E,测得;
(3)在的延长线方向确定点D,使得;
(4)确定点C、点A和点E三点共线,测得;(5)测得 .
任务一
请你根据上述测量方案及数据,求出的长;
任务二
请你证明 .
-
8、某商店购进奥运会吉祥物和纪念币两种纪念品,若购进吉祥物10个、纪念币5个,需要100元;若购进吉祥物5个、纪念币3个,需要55元.(1)、求购进吉祥物,纪念币两种纪念品每件各需多少元?(2)、若该商店计划购进这两种纪念品共50件,且预算不多于400元,则该商店最少购进吉祥物多少件?
-
9、如图,在中, , , 点D是边上动点,(不与点A、点B重合),连接 , 将线段绕点C顺时针旋转至位置,连接 .
 (1)、求的度数;(2)、若 , 当点D在的中点时,求四边形的周长.
(1)、求的度数;(2)、若 , 当点D在的中点时,求四边形的周长. -
10、如图,在中,点E在边上, , 点D在右侧,连接 , , 若 , .
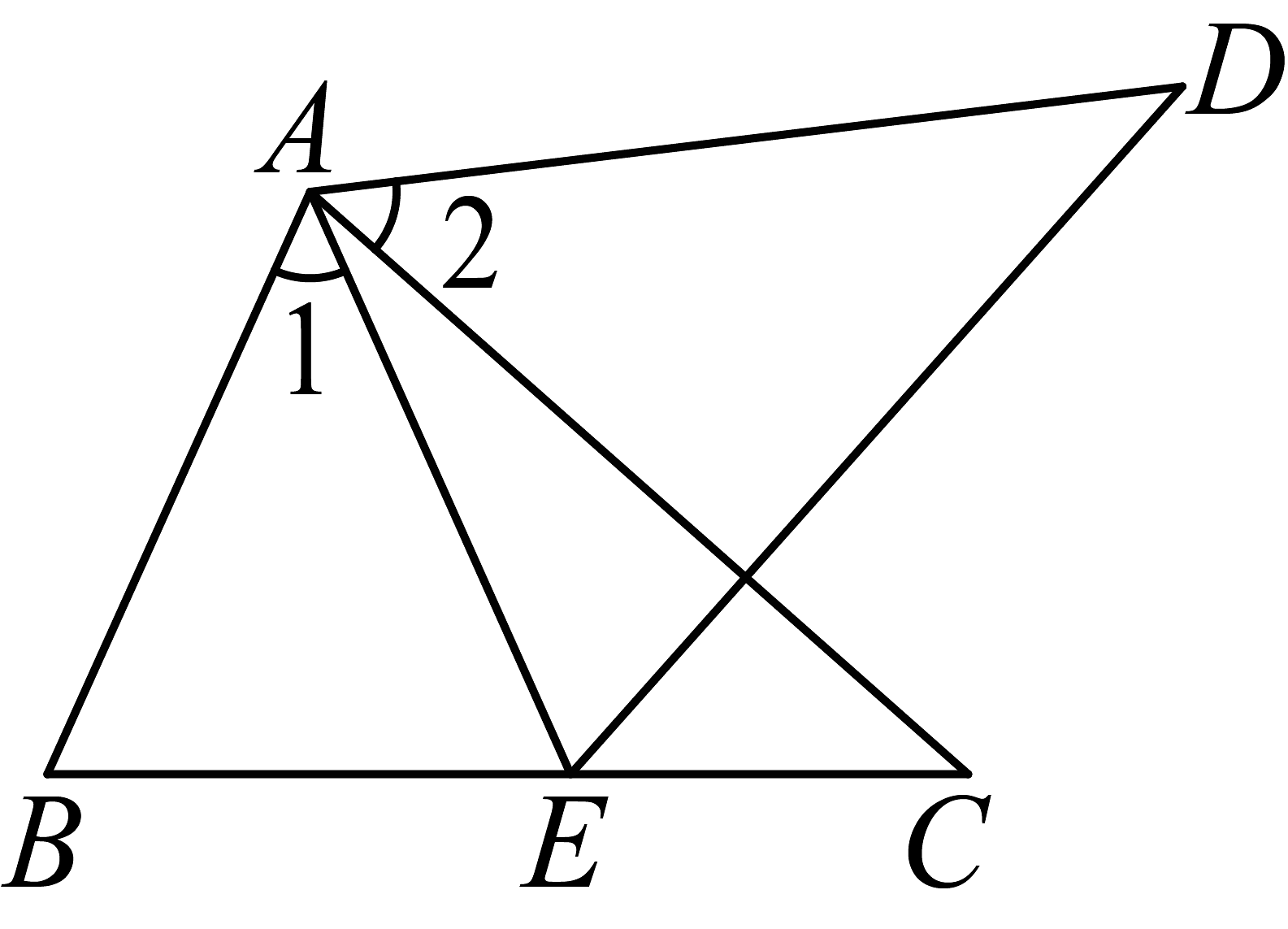
求证: .
-
11、如图,中, , , 的垂直平分线交于点E,交于点D,连接 .
 (1)、求的度数;(2)、若 , 求长.
(1)、求的度数;(2)、若 , 求长. -
12、(1)解不等式: , 并将解集表示在下列数轴上;

(2)解不等式组:
-
13、如图,中, , , , D是线段上一个动点,以为边在外作等边 , 若是的中点,连结 , 当取最小值时,的周长为 .
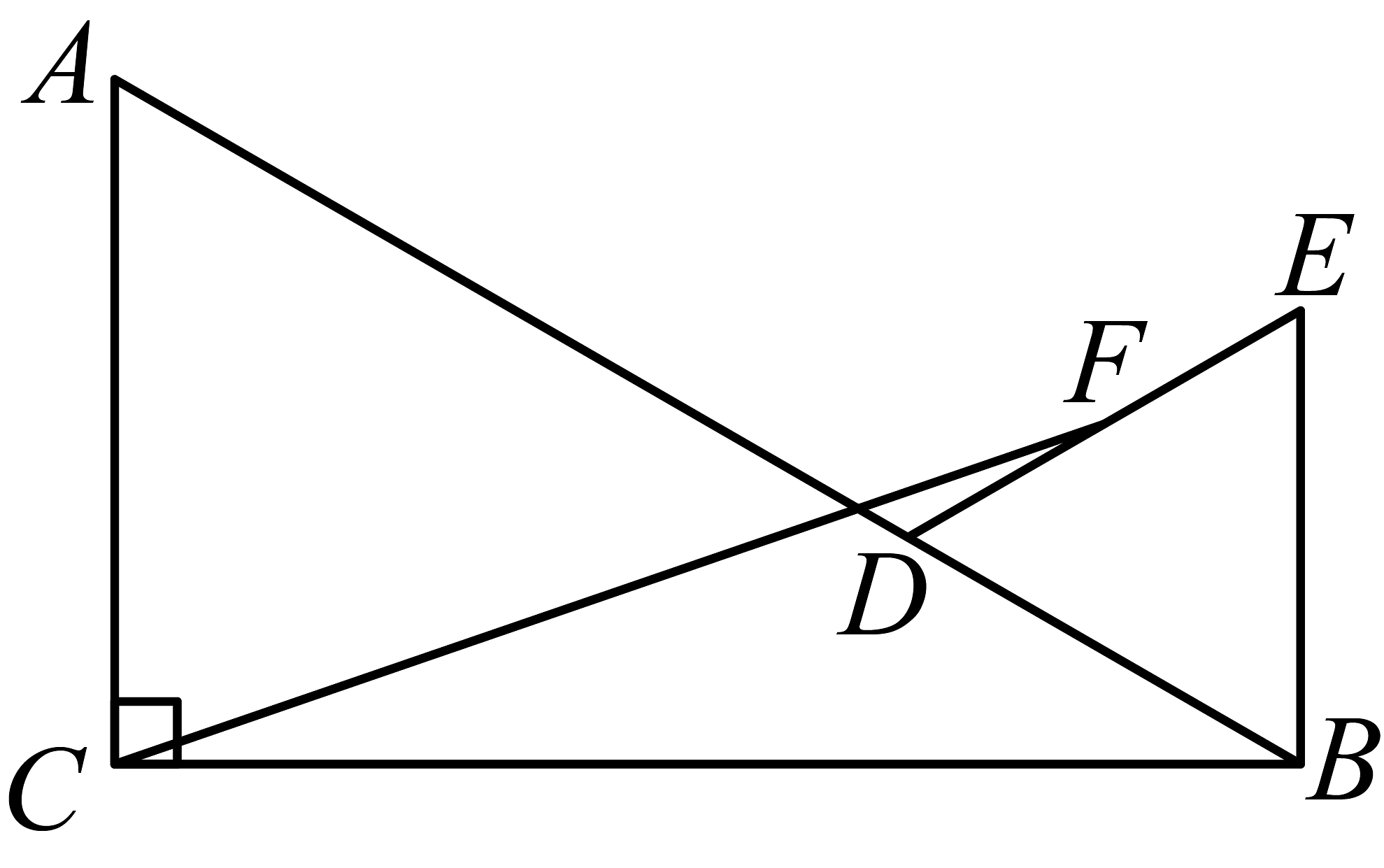
-
14、在边长为和的长方形中作等腰三角形,使得等腰三角形的两个顶点是长方形的顶点,第三个顶点落在长方形的边上,则所画三角形的面积为 .
-
15、美美和小仪到超市购物,且超市正在举办摸彩活动,单次消费金额每满100元可以拿到1张摸彩券.已知美美一次购买5盒饼干拿到3张摸彩券;小仪一次购买5盒饼干与1个蛋糕拿到4张摸彩券.若每盒饼干的售价为x元,每个蛋糕的售价为150元,则x的范围为 .
-
16、如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中 , , 则的值是 .

-
17、将一副三角板如图叠放在一起,则图中的度数为 .

-
18、如图,在中, , 边上的中线 . 过点A作于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、如图是的正方形网格,的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出与成轴对称的格点三角形个数为( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
20、如图, , 动点P满足 , 则的最小值为( )
 A、5 B、 C、 D、
A、5 B、 C、 D、