相关试卷

1、用适当方法解下列方程：

(1)、 $x^{2} + 4 x - 12 = 0$ ；

(2)、 $x + 5 = x^{2} - 25$ ．

查看解析
2、方程 $x^{2} + 4 x - 5 = 0$ 的解是 $x_{1} = 1$ ， $x_{2} = - 5$ ，现在给出另一个方程 ${(2 x - 1)}^{2} + 4 (2 x - 1) - 5 = 0$ ，它的解是．

查看解析
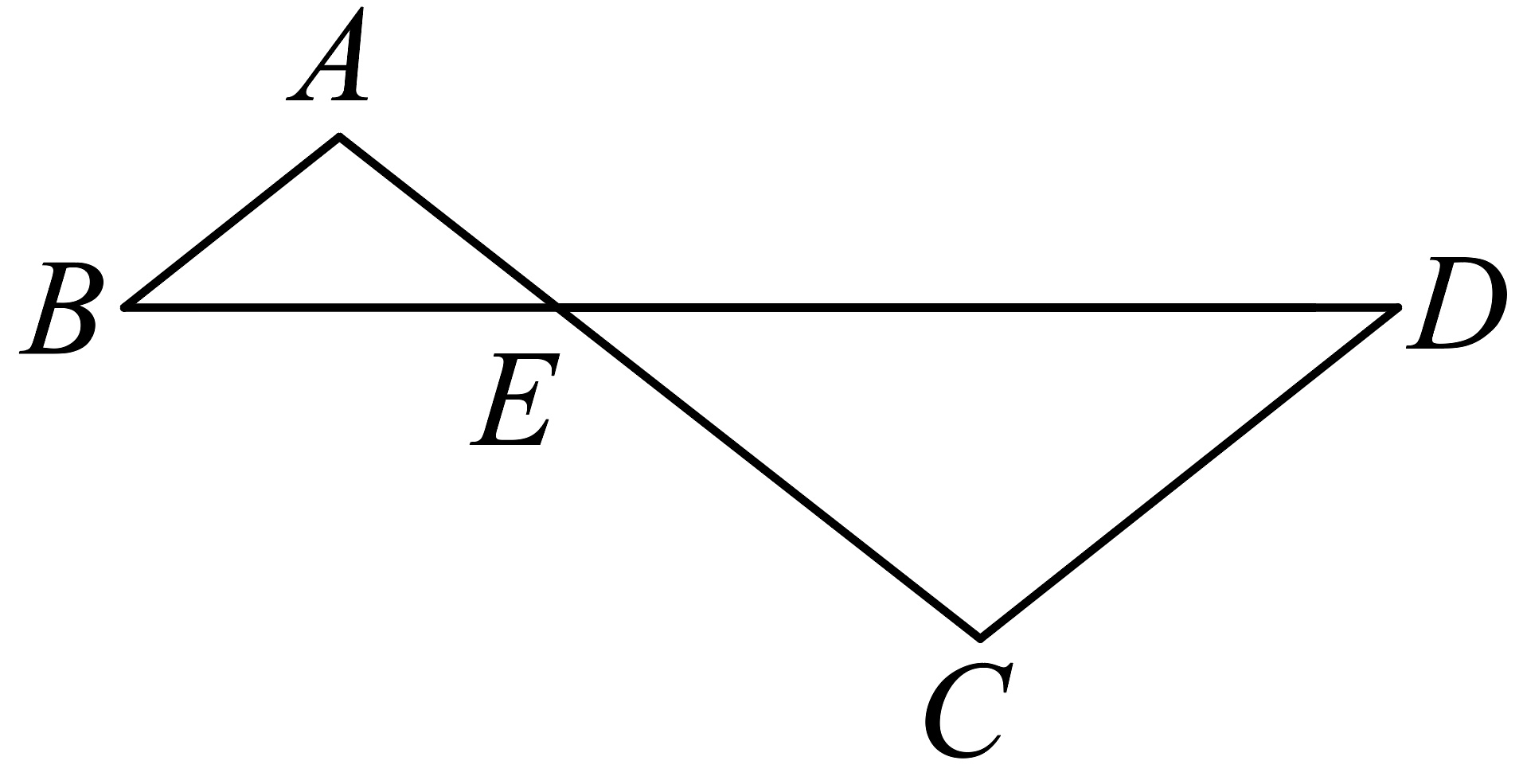
3、如图，AB $∥$ CD，AC，BD相交于点E，AE＝1，EC＝2，DE＝3，则BE的长为．

查看解析
4、在函数 $y = \frac{2024}{x - 5}$ 中，自变量 $x$ 的取值范围是．

查看解析
5、有一名初中生，前两年学习不够努力．进入初三后，在老师和同学的帮助下，逐渐意识到学习的重要性和紧迫性，勤奋苦读，成绩突飞猛进．已知他初二下学期期末考试数学成绩为73分，初三第一次和第二次测试成绩均进步明显，第二次成绩为118分．假定两次增长率相同，设每次平均增长率为 $x$ ，可列方程为（）

A、 $73 + 2 x = 118$ B、 $73 (1 + x^{2}) = 118$ C、 $73 {(1 + x)}^{2} = 118$ D、 $1 + x + x^{2} = 118$

查看解析
6、若 $x = \frac{4 \pm \sqrt{{(- 4)}^{2} - 4 \times 1 \times 3}}{2}$ 是某个一元二次方程的根，则这个方程是（）

A、 $x^{2} + 4 x - 3 = 0$ B、 $x^{2} - 4 x - 3 = 0$ C、 $x^{2} - 4 x + 3 = 0$ D、 $x^{2} + 4 x + 3 = 0$

查看解析
7、已知a、b、c、d是成比例线段，其中 $a = 2 cm$ ， $b = 3 cm$ ， $c = 6 cm$ ，则线段d的长为（）

A、 $3 cm$ B、 $4 cm$ C、 $6 cm$ D、 $9 cm$

查看解析
8、下列函数中，表示 $y$ 是 $x$ 的反比例函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = - \frac{1}{x}$ C、 $y = 2 x$ D、 $y = x + 2$

查看解析
9、一元二次方程 $2 x^{2} - 4 x + 1 = 0$ 的二次项系数为2，则一次项系数是（）

A、1 B、4 C、 $- 4$ D、 $- 1$

查看解析
10、广东省2023年农产品进出口总额居全国首位，其中荔枝鲜果远销欧美．已知某品种荔枝的成本价为每千克20元．品种每天的销量y（千克）与销售价x（元/千克）有如下关系： $y = - 2 x + 80$ ．设该品种荔枝每天的销售利润为W元．

(1)、诸写出利润W与销售价x之间的函数关系式：　　；

(2)、该产品销售价格为每千克多少元时，每天的销售利润最大？最大利润是多少元？

(3)、如果物价部门规定这种产品的销售价不高于每千克28元，要想获得每天150元的销售利润，销售价应定为每千克多少元？

查看解析
11、已知在 $△ A B C$ 中，底边 $B C$ 与对应的高 $A D$ 的长度之和为30．

(1)、设 $B C$ 边长为x，直接写出 $△ A B C$ 的面积S与x的函数关系式　　，其中x的取值范围是　　；

(2)、当 $B C =$ 　　时， $△ A B C$ 的面积达到最大，最大值是　　；

(3)、当底边 $B C$ 与高 $A D$ 的比值为2：1时（如图），其周长是否有最小值？如果有，请求出；如果没有，请说明理由．

查看解析
12、如图，抛物线 $y = - x^{2} + m x$ 与直线 $y = x + b$ 交于点A和点B，直线 $A B$ 与y轴交于点 $C (0, - 2)$ ．

(1)、求直线和抛物线的解析式；

(2)、求点A的坐标，并结合函数图象，求出不等式 $- x^{2} + m x > x + b$ 的解集．

查看解析
13、二次函数 $y = a x^{2} + b x - 3$ 中的x，y满足下表：
x
…
$- 1$
0
1
2
3
…
$y = a x^{2} + b x - 3$
…
0
$- 3$
$- 4$
$- 3$
0
…

(1)、求此二次函数的解析式；

(2)、若 $y \geq - 3$ ，请直接写出x的取值范围．

查看解析
14、选择适当的方法解下列方程：

(1)、 $x^{2} - 7 x - 8 = 0$ ；

(2)、 $x^{2} - 2 \sqrt{3} x + 1 = 0$ ．

查看解析
15、无论x取任何实数，代数式 $\sqrt{x^{2} - k x + 3}$ 都有意义，则k的取值范围为．

查看解析
16、如果一条抛物线的形状与 $y = \frac{1}{2} x^{2} + 2$ 的形状和开口方向均相同，且顶点坐标是 $(- 4 ， 2)$ ，那么它的函数解析式为．

查看解析
17、已知二次函数 $y = - x^{2} + 2 x + 3$ ，当 $- 1 \leq x \leq 2$ 时， $y$ 的最大值与最小值之和为．

查看解析
18、抛物线 $y = (x + 5) (x - 1)$ 的对称轴为．

查看解析
19、如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于点 $(- 3, 0)$ ，其对称轴为直线 $x = - \frac{1}{2}$ ，结合图象分析下列结论：
① $a b c > 0$ ；
②对于任意实数m，都有 $\frac{1}{4} a - \frac{1}{2} b \leq a m^{2} + b n$ ；
③当 $x < 0$ 时，y随x的增大而增大；
④ $3 a + 3 b + c = 0$ ；
⑤若 $x_{1}, x_{2} (x_{1} < x_{2})$ 为方程 $a (x + 3) (x - 2) = 1$ 的两个根，则 $- 3 < x_{1} < x_{2} < 2$ ．
其中正确结论的个数有（　　）个．

A、1 B、2 C、3 D、4

查看解析
20、已知抛物线 $y = {(x - 1)}^{2} + 5$ ，平移后得到新的抛物线 $y = x^{2} + 2 x + 6$ ，则水平平移的方向和距离为（　　）

A、向左平移3个单位 B、向右平移3个单位 C、向左平移2个单位 D、向右平移2个单位

查看解析

上一页 346 347 348 349 350 下一页跳转

x	…	$- 1$	0	1	2	3	…
$y = a x^{2} + b x - 3$	…	0	$- 3$	$- 4$	$- 3$	0	…