相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、已知直线与相切于点 , 连接交于点 .
(1)如图①,点是优弧上一点,连接 , 若 , 则;
(2)如图②,延长交于点 , 连接 , 若 , 则;
(3)如图③,点是上一点,且 , 连接并延长交于点 , 连接 , 若 , 则 .

-
2、某种麦粒在相同条件下进行发芽试验,结果如下表所示,则任取一粒麦粒,估计它能发芽的概率约为 . (结果精确到)
试验的麦粒数
发芽的麦粒数
发芽的频率
-
3、已知锐角中,O是的中点,小明、小英二人想在线段上找一点P,使得为直角,其作法如图.对于小明、小英二人的作法,正确的是( )
小明的作法

过点B作与垂直的直线,交于点P,则P即为所求
小英的作法
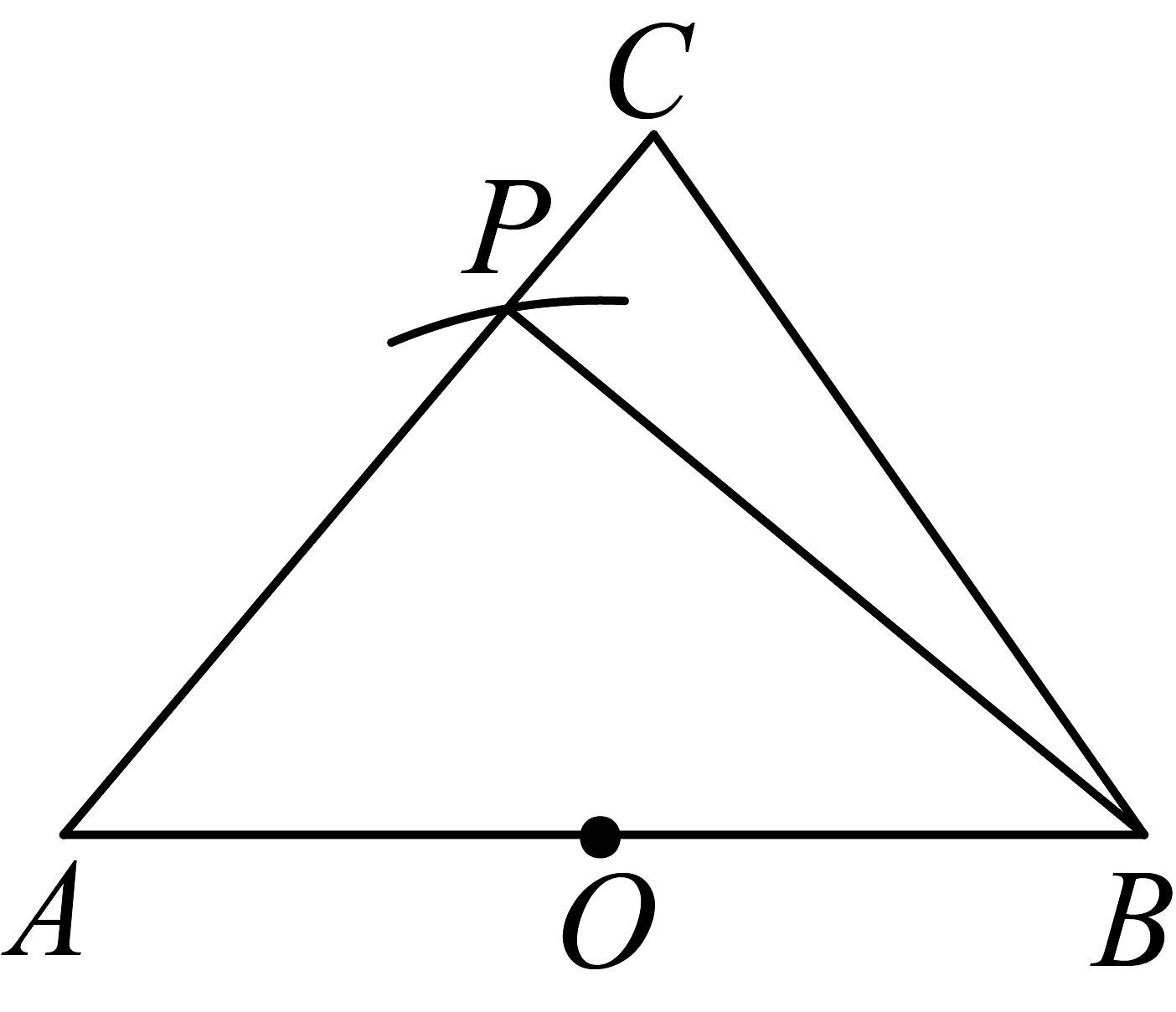
以O为圆心,长为半径画弧,交于点P,则P即为所求
A、只有小明正确 B、只有小英正确 C、两人都正确 D、两人都不正确 -
4、如图,中, . 将绕点B逆时针旋转得到 , 点C的对应点落在边上, , 连接 . 则长为( )
 A、 B、 C、3 D、4
A、 B、 C、3 D、4 -
5、全班共有名学生,其中有名女生,位男生,班级需选出一名女生参加升旗仪式,在女生中选到王芳的概率为( )A、 B、 C、 D、
-
6、关于x的方程有实数根,则k的取值范围是( )A、 B、 C、 D、
-
7、下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
8、综合与实践
【问题情境】
某综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作长方体纸盒.
【操作探究】
(1)、若准备制作一个无盖的正方体纸盒,图1中的 图形经过折叠能围成无盖正方体纸盒.(2)、图2是嘉嘉的设计图,把它折成无盖正方体纸盒后与“保”字相对的是 字.(3)、如图3,有一张边长为的正方形废弃宣传单,嘉嘉准备将其四个角各剪去一个小正方形,折成无盖长方体纸盒,折成的纸盒高为 .①四角应各剪去边长为 的小正方形;
②计算此长方体纸盒的容积.
(4)、根据如图4方式制作一个有盖的长方体纸盒.方法:先在边长为的正方形纸板四角剪去两个边长为的小正方形和两个同样大小的小长方形,再沿虚线折叠起来.该长方体纸盒的体积为多少?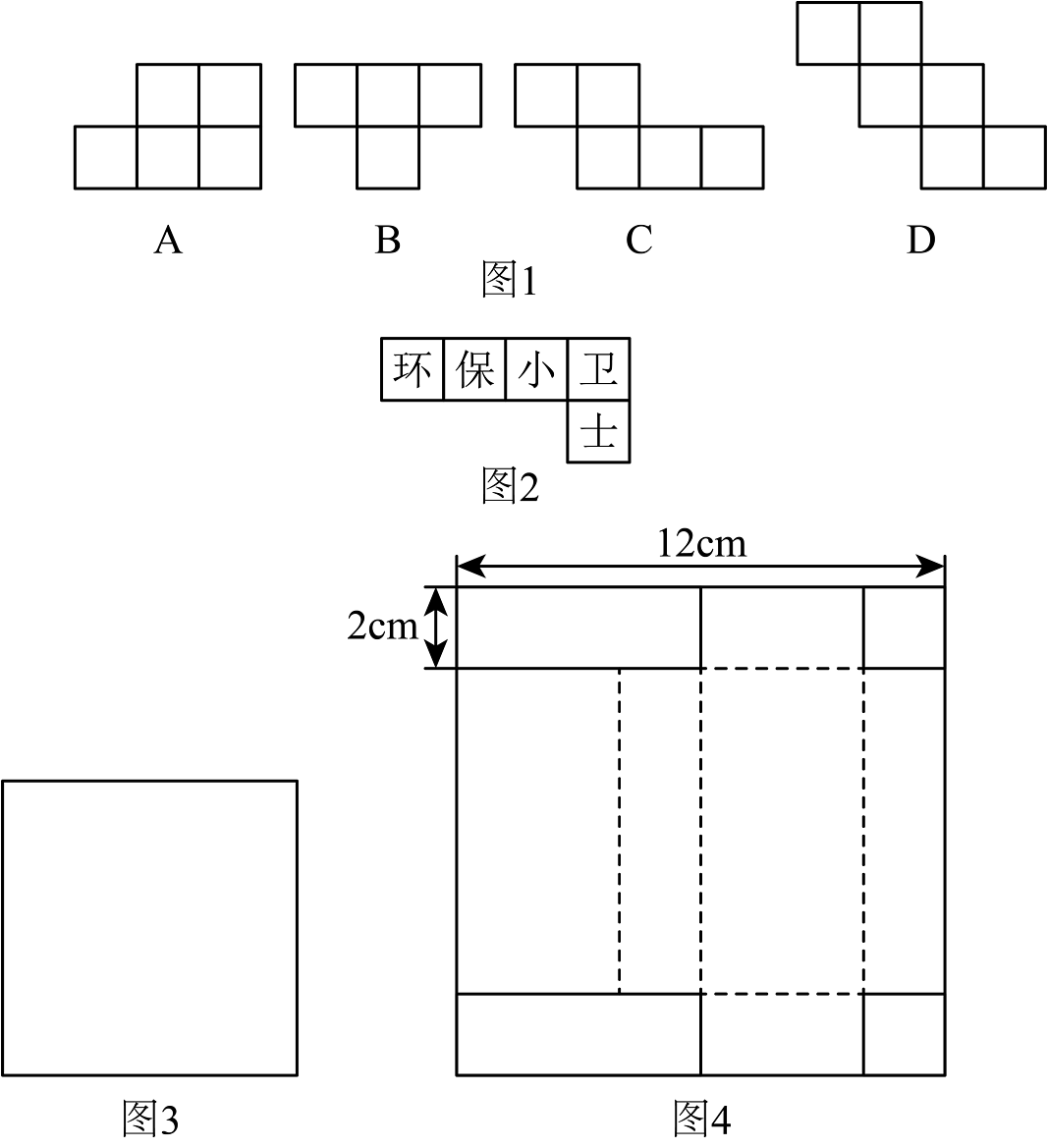
-
9、已知关于、的多项式 .(1)、求;老师展示了一位同学的作业如下:
解: 第一步
第二步
第三步
回答问题:这位同学第 步开始出现错误,错误原因是 ;
(2)、若的结果与字母的取值无关,求的值. -
10、化简并求值: , 其中x、y取值的位置如图所示.
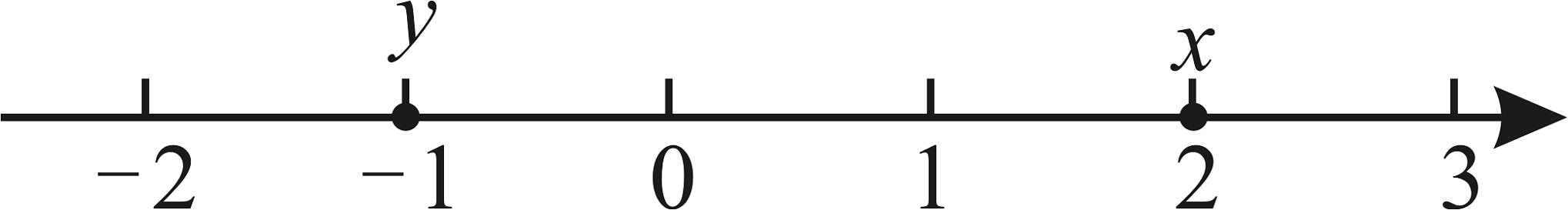
-
11、计算: .
-
12、已知 , 则 .
-
13、单项式的系数是 .
-
14、在某月的日历上用长方形圈到a,b,c,d四个数(如图),如果 , 那么的值为( )
 A、22 B、25 C、29 D、30
A、22 B、25 C、29 D、30 -
15、下列个数、、、、、每两个之间依次一个、 , 其中有理数有( )个A、3 B、4 C、5 D、6
-
16、在 , , , 这四个数中,最小的数是( )A、 B、 C、 D、
-
17、当时,整式的值为 , 则当时,整式的值为( )A、 B、 C、 D、无法确定
-
18、如图,在数轴上点A,B,C分别表示的数为a,b,c.已知a,b分别是多项式的次数和常数项,c是单项式的系数.
 (1)、填空:______,______,______;并在数轴上标出原点O;(2)、若动点M,N分别从点A,B同时出发沿数轴向左运动,点M的速度是每秒2个单位长度,点N的速度是每秒1个单位长度,求运动几秒后,点M可以追上点N?(3)、若动点P从原点O出发,以每秒3个单位长度的速度向左运动,同时另一动点Q从点A出发,以每秒2个单位长度的速度向左运动,到达原点后立即以原来的速度返回,向右运动.设运动的时间为t秒,当点Q到原点O的距离为3时,求点P表示的数.
(1)、填空:______,______,______;并在数轴上标出原点O;(2)、若动点M,N分别从点A,B同时出发沿数轴向左运动,点M的速度是每秒2个单位长度,点N的速度是每秒1个单位长度,求运动几秒后,点M可以追上点N?(3)、若动点P从原点O出发,以每秒3个单位长度的速度向左运动,同时另一动点Q从点A出发,以每秒2个单位长度的速度向左运动,到达原点后立即以原来的速度返回,向右运动.设运动的时间为t秒,当点Q到原点O的距离为3时,求点P表示的数. -
19、已知的值与字母x的取值无关,求代数式的值.
-
20、星光中学召开秋季运动会,七(1)班同学准备统一购买运动鞋和运动服.已知 , 两家运动品牌店的一款运动鞋每双元,运动服每套元.国庆期间,这两家店都开展促销活动,如下:
A店:买套运动服送一双运动鞋;
B店:运动服原价,运动鞋打六五折.
若七(1)班要购买运动服套,运动鞋双(大于).
(1)、分别求出七(1)班在店,店购买时,所要付款的金额;(用含的代数式表示)(2)、当时,请你通过计算说明到哪家店购买更划算?