相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、如图,A,B,C是上的三点,且 , 则的度数是( )
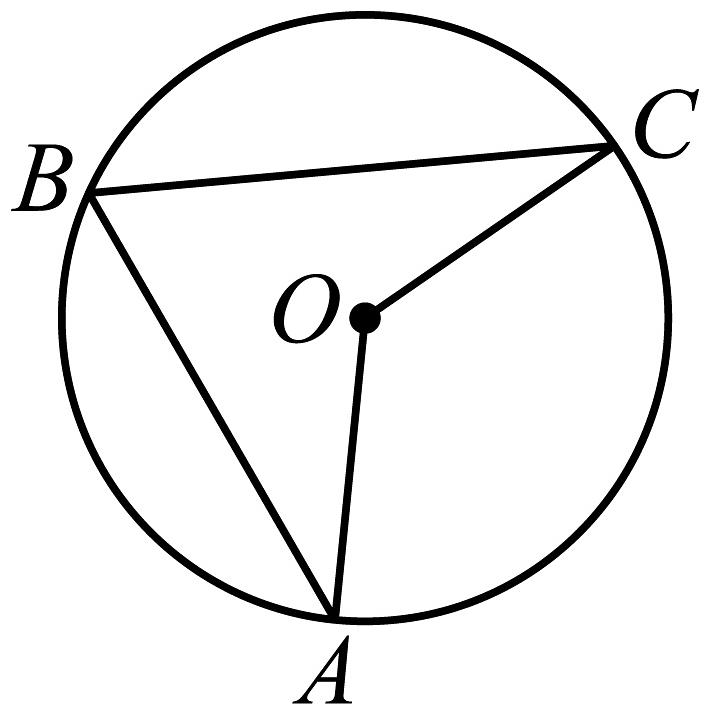 A、 B、 C、 D、或
A、 B、 C、 D、或 -
2、如图,与关于成中心对称,下列结论中不成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、将二次函数的图象向右平移4个单位长度,再向上平移5个单位长度后,所得图象对应的函数解析式是( )A、 B、 C、 D、
-
4、下列方程是一元二次方程的是( )A、 B、 C、 D、
-
5、综合与实践:【问题情境】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系.数学活动课上,王老师出示了一个问题:点、在数轴上分别表示有理数、 , 则在数轴上、两点之间的距离为 . 如:表示为3与1两数在数轴上所对应的两点之间的距离;表示为3与两数在数轴上所对应的两点之间的距离.

利用数形结合思想回答下列问题:
(1)数轴上表示2和7两点之间的距离是______;数轴上表示2和的两点之间的距离是______;
【解决问题】:
(2)数轴上表示和的两点之间的距离表示为______.
(3)试用数轴探究:当时的值为______.
【实践探究】利用绝对值的几何意义,结合数轴,探究:
(4)利用数轴求出的最小值为______,并写出此时可取的整数值为______.
-
6、【阅读材料】“整体思想”是中学数学解题中的一种重要的思想方法,运用“整体思想”的方法在求代数值中非常重要,有这样一道题:
代数式:的值为9,则代数式的值为.
小明在做作业时采用的方法如下:
由题意得 , 则有 .
所以
.
所以代数式的值为9.
【方法运用】
(1)、若 , 则______.(2)、若代数式的值为15,求代数式的值. -
7、一天下午,某出租车以希望小学为出发点在东西方向营运,行车情况依先后次序记录如下(向东为正方向,单位:):
, , , , , , , .
(1)、将最后一名乘客送到目的地,出租车在出发点位置的东边还是西边?离出发点多远?(2)、若出租车在行驶过程中,每千米耗油升,出租车一下午共耗油多少升? -
8、小明同学在学习完有理数的运算后,对运算产生了浓厚的兴趣,她借助有理数的运算,定义了一种新运算“”,运算规则为: . 如:(1)、求的值;(2)、求的值.
-
9、已知互为相反数,互为倒数,是最大的负整数,求的值.
-
10、在数轴上表示下列各数,并用“<”把这些数连接起来.

;3.5;; .
-
11、计算:(1)、(2)、
-
12、如果电梯上升5米,记作+5米,那么下降8米可记作米.
-
13、根据流程图中的运算程序,当输入数据时,输出结果为( )
 A、9 B、 C、25 D、
A、9 B、 C、25 D、 -
14、如图,将刻度尺放在数轴上,让和刻度线分别与数轴上表示2和4的两点重合对齐,则数轴上与刻度线对齐的点表示的数为( )
 A、 B、0 C、1 D、2
A、 B、0 C、1 D、2 -
15、一个两位数,十位上的数字是 , 个位上的数字是 , 这个两位数是( )A、 B、 C、 D、
-
16、在 , 2024, , 四个数中有理数的个数是( )A、1个 B、2个 C、3个 D、4个
-
17、南岸区是一个充满生机和活力的市区,它古老而又年轻,区域内人口约为1200000人.则1200000用科学记数法可表示为( )A、 B、 C、 D、
-
18、某出租车公司推出专车和快车两种出租车,它们的收费方式如下:
专车:千米以内收费元,超过千米的部分每千米收费元,不收其他费用;
快车:
计费项目
起步价
里程费
远途费
计费价格
元
2元/千米
1元/千米
注:车费由起步价、里程费、远途费三部分组成,其中起步价包含里程千米;里程大于千米的部分按计价标准收取里程费;远途费的收取方式为:行车不超过12千米,不收远途费,超过千米的,超出的部分每千米加收元.
(1)、如果乘车路程是千米,使用专车、快车出行各需支付费用多少元?(2)、如果乘车路程是千米,使用专车、快车出行各需支付的费用多少元(用含的式子表示)?(3)、如果乘车路程是千米时,使用快车出行的费用比使用专车出行省4元,求的值. -
19、定义:对于一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“相异数”,将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数,将这个新两位数与原两位数求和,同除以11所得的商记为 . 例如, , 对调个位数字与十位数字得到的新两位数51,新两位数与原两位数的和为 , 和66除以11的商为 , 所以 .(1)、计算:____;(2)、若一个“相异数”的十位数字是 , 个位数字是 , 且 , 求相异数;(3)、小慧同学发现若 , 则“相异数”的个位数字与十位数字之和一定为7,请判断小慧的发现是否正确?如果正确,说明理由;如果不正确,举出反例.
-
20、手工制作课上,劳动课吴老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有48人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身55个或剪筒底130个.(1)、七年级(2)班有男生、女生各多少人?(2)、七年级(2)班全体同学积极参与制作圆柱形茶叶筒,要求用一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?