相关试卷

1、计算：

(1)、 $\frac{5}{17} - (+ 9) - 12 - (- \frac{12}{17}) ；$

(2)、4.25+(-2.18)-(-2.75)+5.18；

(3)、 $\frac{5}{6} + (- \frac{3}{4}) - ∣ - 0.25 ∣ - (- \frac{1}{6}) ；$

(4)、 $∣ - 16.2 ∣ + ∣ - 2 \frac{1}{3} ∣ + [- (- 3 \frac{2}{3}] - ∣ 10.7 ∣ .$

查看解析
2、计算：

(1)、 $1 \frac{1}{2} - 1 \frac{1}{4} + 3 \frac{3}{4} - 0.25 - 3.75 - 4.5 ；$

(2)、 $12 \frac{1}{4} - (+ 1.75) - (- 5 \frac{1}{2}) + (- 7.25) - (- 2 \frac{3}{4}) - 2.5 .$

查看解析
3、计算：

(1)、8+(-4)+6+4+12+(-8)+(-2)；

(2)、36.54+22.57+63.46+(-10.57).

查看解析
4、将一串正负数按如下规律排列，回答下列问题.

(1)、在A 位置的数是正数还是负数?

(2)、A，B，C，D 中哪些位置的数是负数?

(3)、第2046个数是正数还是负数?排在A，B，C，D 中哪个位置?

查看解析
5、观察下列数后，找出规律，并填空：
$- 1 ， \frac{1}{2} ， - \frac{1}{3} ， \frac{1}{4} ， - \frac{1}{5} ， \frac{1}{6} ，$ ，， $\dots ，$ (第100个数).

查看解析
6、请将下列各数：0.6，-3，+2，10%，0，-8，-1.2，+ $\frac{3}{2}$ ， π，- $\frac{1}{3}$ ， 0.3填入相应的括号内.

(1)、自然数{           }；

(2)、负整数{           }；

(3)、非负数{           }；

(4)、正分数{           }；

(5)、负分数{           }；

(6)、有理数{           }.

查看解析
7、观察下面一列数：-1，2，-3，4，-5，6，-7，…，将这列数排成下图形式：

(1)、按照上述规律排下去，第9行最右边的数是；

(2)、第10行从左向右数第10个数是；

(3)、2 024 这个数是第行从左往右数的第个数.

查看解析
8、观察下列数后，找出规律，并填空：
1，-2，-3，4，5，-6，-7，8，，， …，(第 2 024个数).

查看解析
9、将下列各数按一定标准分类，再把它们填写在相应集合圈内：0.618，+3.14，2024，10%，0，-8，-1.2，+5，-π，- $\frac{2}{3}$

查看解析
10、在一堂函数专题复习课上，刘老师给出了新定义：若两个函数的图象关于某一点P成中心对称，则称这两个函数关于点P互为“对称函数”．请同学们解决以下问题：

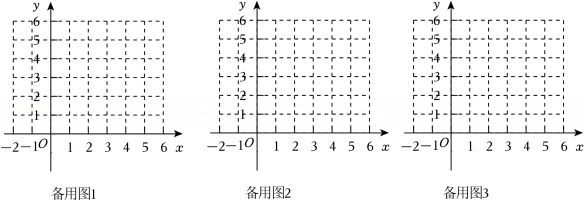(1)、求函数y＝x﹣1关于点（0，0）的“对称函数”．小乐同学给出了如下的解题步骤：
第一步：在函数y＝x﹣1的图象上取两点（1，0）和（0，﹣1）；
第二步：分别求出这两个点关于点（0，0）的对称点和；
第三步：函数y＝x﹣1关于点（0，0）的“对称函数”为．

(2)、是否存在点P，使得函数y $= \frac{1}{x} +$ 1关于点P的“对称函数”就是它本身？如果存在，请求出点P的坐标；如果不存在，请说明理由；

(3)、函数C₁：y＝ax²﹣2ax+2a（a＞0）关于点（2，2）的“对称函数”为C₂ ，函数C₁与函数C₂所围成的区域（包括边界）记作W，横坐标、纵坐标都为整数的点叫做“整点”．
（i）若a $= \frac{1}{2}$ ，求W内的“整点”个数；
（ii）若W内至少有9个“整点”，至多有13个“整点”，求a的取值范围．

查看解析
11、两千多年前，古希腊数学家欧多克索斯发现：将一条线段AB分割成长、短两条线段AC、CB，若短段与长段的长度之比等于长段的长度与全长之比，即 $\frac{C B}{A C} = \frac{A C}{A B}$ ，则这种分割称为黄金分割，这个比值称为黄金比，点C叫做线段AB的黄金分割点．

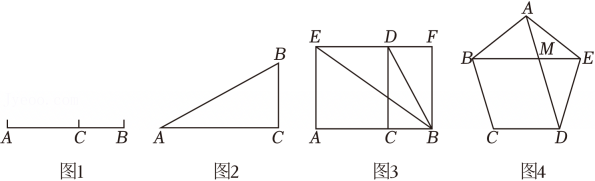(1)、【问题初探】
如图1，已知点C为线段AB的黄金分割点（AC＞BC），求黄金比．
解：设AB＝1，AC＝x，则CB＝1﹣x．
∵ $\frac{C B}{A C} = \frac{A C}{A B}$ ，
∴⋯⋯
请补全以上解题过程；

(2)、【问题再探】
如图2，在Rt△ABC中，∠C＝90°，BC＝1，AC＝2，请作出AC的黄金分割点（要求：仅用圆规作图，不写作法，保留作图痕迹）；

(3)、【知识迁移】
如图3，点C为线段AB的黄金分割点（AC＞BC），分别以AC、BC为边在线段AB同侧作正方形ACDE和矩形CBFD，连结BD、BE．求证：△EAB∽△BCD；

(4)、【延伸拓展】
如图4，在正五边形ABCDE中，对角线AD与BE交于点M．求证：点M是AD的黄金分割点．

查看解析
12、如图，⊙O为△ABD的外接圆，直径AB垂直于弦DE，垂足为点F．点C为圆外一点，连结BE、BC、CD，∠DBC＝∠DEB．

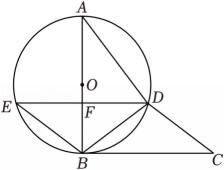(1)、求证：BC为⊙O的切线；

(2)、若BE∥CD，tanC $= \frac{3}{4}$ ， CD＝5，求OF的长．

查看解析
13、如图，一次函数y＝x﹣1的图象与反比例函数y $= \frac{k}{x}$ （k≠0）的图象交于点A（m，1）、B（﹣1，n）．

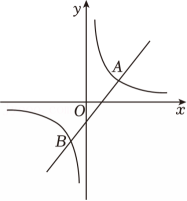(1)、求m、n的值和反比例函数的表达式；

(2)、若在x轴上存在点P（a，0），使得△ABP的面积为6，求a的值．

查看解析
14、如图，在△ABC中，∠ABC＝45°，∠ACB＝60°，AC＝2．

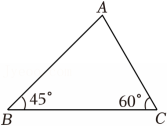(1)、求AB的长；

(2)、求点C到线段AB的距离．

查看解析
15、某校开展“综合与实践”项目学习，拟开设四个项目供学生选择：A．体育中的数学，B．绘制公园平面地图，C．改进我们的课桌椅，D．高度的侧量．若每名学生只选择其中一个项目进行学习，现随机调查部分学生的选择情况并绘制成统计图表．如图所示．
项目
人数
频率
A
16
B
8
C
D
4
0.1
根据以上信息，解答下列问题：

(1)、本次调查抽取的学生总人数为 ▲ 人，请补全条形统计图；

(2)、已知该校共有800名学生，请估计选择项目B的学生人数；

(3)、现准备从四个项目中随机选择两个项目在全校作汇报展示，请利用画树状图或列表的方法，求恰好选到项目A和项目B的概率．

查看解析
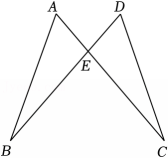
16、如图，已知线段AC、BD相交于点E，AE＝DE，BE＝CE．求证：AB＝DC．

查看解析
17、先化简，再求值：（x+3）²+3x（x﹣2），其中x $= \frac{1}{2}$ ．

查看解析
18、解不等式组： $\{\begin{array}{l} x + 1 ＞ - 1 \\ 3 (x - 2) \leq 2 x - 3 \end{array}$ ．

查看解析
19、计算：|﹣3| $+ \sqrt{25} -$ 2sin30°．

查看解析
20、定义：在平面直角坐标系中，到原点的距离等于1的点叫做“单位圆点”．
⑴下列三个函数的图象上存在“单位圆点”的是（填番号）；
①y＝x+2；
②y $= \frac{1}{x}$ ；
③y＝x²+1．
⑵若一次函数y $= \frac{1}{2}$ x+m的图象上存在“单位圆点”，则m的取值范围为．

查看解析

上一页 750 751 752 753 754 下一页跳转

项目	人数	频率
A	16
B	8
C
D	4	0.1