2017年山东省聊城市冠县中考数学三模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
1. 16的算术平方根是( )A、16 B、4 C、﹣4 D、±42. 如图,已知直线a、b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
 A、150° B、120° C、60° D、30°3. 下面的几何体中,俯视图为三角形的是( )A、
A、150° B、120° C、60° D、30°3. 下面的几何体中,俯视图为三角形的是( )A、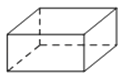 B、
B、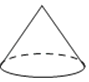 C、
C、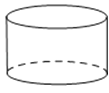 D、
D、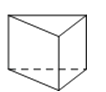 4. 因式分解3y2﹣6y+3,结果正确的是( )A、3(y﹣1)2 B、3(y2﹣2y+1) C、(3y﹣3)2 D、5. 如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
4. 因式分解3y2﹣6y+3,结果正确的是( )A、3(y﹣1)2 B、3(y2﹣2y+1) C、(3y﹣3)2 D、5. 如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )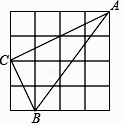 A、 B、 C、 D、26. 下列函数中,当x>0时,y的值随x的值增大而增大的是( )A、y=﹣x2 B、y=x﹣1 C、y=﹣x+1 D、y=7. 小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是( )A、掷一次骰子,在骰子向上的一面上的点数大于0 B、掷一次骰子,在骰子向上的一面上的点数为7 C、掷三次骰子,在骰子向上的一面上的点数之和刚好为18 D、掷两次骰子,在骰子向上的一面上的点数之积刚好是118. 下列命题:
A、 B、 C、 D、26. 下列函数中,当x>0时,y的值随x的值增大而增大的是( )A、y=﹣x2 B、y=x﹣1 C、y=﹣x+1 D、y=7. 小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是( )A、掷一次骰子,在骰子向上的一面上的点数大于0 B、掷一次骰子,在骰子向上的一面上的点数为7 C、掷三次骰子,在骰子向上的一面上的点数之和刚好为18 D、掷两次骰子,在骰子向上的一面上的点数之积刚好是118. 下列命题:⑴有一个角是直角的四边形是矩形;
⑵一组邻边相等的平行四边形是菱形;
⑶一组邻边相等的矩形是正方形;
⑷一组对边平行且相等的四边形是平行四边形.
其中真命题的个数是( )
A、0个 B、1个 C、2个 D、3个9. 已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为( )A、(3,0) B、(3,﹣3) C、(3,﹣1) D、(﹣1,3)10. 二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )A、y=(x﹣1)2+2 B、y=(x﹣1)2+3 C、y=(x﹣2)2+2 D、y=(x﹣2)2+411. 在平面直角坐标系中直线y=x+2与反比例函数 y=﹣ 的图象有唯一公共点,若直线y=x+m与反比例函数y=﹣ 的图象有2个公共点,则m的取值范围是( ) A、m>2 B、﹣2<m<2 C、m<﹣2 D、m>2或m<﹣212. 下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )
A、m>2 B、﹣2<m<2 C、m<﹣2 D、m>2或m<﹣212. 下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )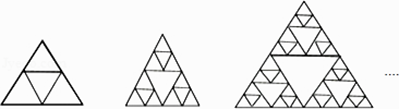 A、160 B、161 C、162 D、163
A、160 B、161 C、162 D、163二、填空题
-
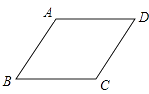
13. 一个样本的50个数据分别落在4个组内,第1、2、3组数据的个数分别是7、8、15,则第4组数据的频率为 .14. 若同时抛掷两枚质地均匀的骰子,则事件“两枚骰子朝上的点数互不相同”的概率是 .15. 关于x的方程kx2﹣4x﹣4=0有两个不相等的实数根,则k的最小整数值为 .16. 若一个圆锥的侧面积是它底面积的2倍,则这个圆锥的侧面展开图的圆心角是 .17. 如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
三、解答题
-
18. 综合题。(1)、计算:|﹣ |+( )﹣1﹣2cos45°.(2)、解方程: + =1.19. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
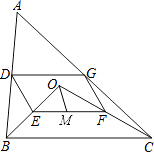 (1)、求证:四边形DEFG是平行四边形;(2)、若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.20. 为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)、求证:四边形DEFG是平行四边形;(2)、若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.20. 为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.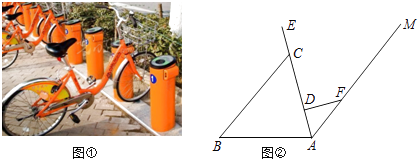 (1)、求AD的长;(2)、求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)21. 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)、求AD的长;(2)、求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)21. 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: (1)、本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;(2)、本次抽样调查中,学习时间的中位数落在哪个等级内?(3)、表示B等级的扇形圆心角α的度数是多少?(4)、在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.22. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.23. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数y= 的图象上.
(1)、本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;(2)、本次抽样调查中,学习时间的中位数落在哪个等级内?(3)、表示B等级的扇形圆心角α的度数是多少?(4)、在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.22. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.23. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数y= 的图象上.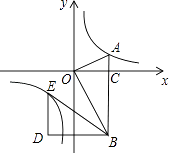 (1)、求反比例函数y= 的表达式;(2)、在x轴的负半轴上存在一点P,使得S△AOP= S△AOB , 求点P的坐标;(3)、若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.24. 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
(1)、求反比例函数y= 的表达式;(2)、在x轴的负半轴上存在一点P,使得S△AOP= S△AOB , 求点P的坐标;(3)、若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.24. 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. (1)、猜想ED与⊙O的位置关系,并证明你的猜想;(2)、若AB=6,AD=5,求AF的长.25. 如图,已知抛物线y=﹣ +bx+c图象经过A(﹣1,0),B(4,0)两点.
(1)、猜想ED与⊙O的位置关系,并证明你的猜想;(2)、若AB=6,AD=5,求AF的长.25. 如图,已知抛物线y=﹣ +bx+c图象经过A(﹣1,0),B(4,0)两点. (1)、求抛物线的解析式;(2)、若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
(1)、求抛物线的解析式;(2)、若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.