2017年山东省济南市天桥区中考数学二模试卷

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

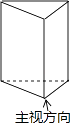
1. ﹣2的绝对值是（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 已知空气的单位体积质量是0.01239g/cm³ ，数据0.001239用科学记数法可表示为（）

A、1.239×10^﹣³ B、1.239×10^﹣² C、0.1239×10^﹣² D、12.39×10^﹣⁴

查看试题解析
3. 下列计算正确的是（）

A、（x+y）²=x²+y² B、（x﹣y）²=x²﹣2xy﹣y² C、x（x﹣1）=x²﹣1 D、（x+1）（x﹣1）=x²﹣1

查看试题解析
4. 如左图所示的正三棱柱，其主视图正确的为（）

A、 B、 C、 D、

查看试题解析
5. 如图，已知∠1=70°，如果CD∥BE，那么∠B的度数为（）

A、70° B、100° C、110° D、120°

查看试题解析
6.
如图为一次函数y=kx+b（k≠0）的图象，则下列正确的是（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
7. 如图，⊙O是△ABC的外接圆，连接OB、OC，若OB=BC，则∠BAC等于（）

A、60° B、45° C、30° D、20°

查看试题解析
8. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为零，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
9. 如图，△DEF是由△ABC通过平移得到，且点B，E，C，F在同一条直线上．若BF=14，EC=6．则BE的长度是（）

A、2 B、4 C、5 D、3

查看试题解析
10. 下列命题是真命题的是（　　）

A、对角线互相平分的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直的四边形是正方形

查看试题解析
11. 表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s² ．
甲
乙
丙
丁
平均数 x（cm）
561
560
561
560
方差s²（cm²）
35
35
155
165
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
12. 新年里，一个小组有若干人，若每人给小组的其它成员赠送一张贺年卡，则全组送贺卡共72张，此小组人数为（　　）

A、7 B、8 C、9 D、10

查看试题解析
13. 已知二次函数y=ax²+bx+c（a＞0）的图象过点A（1，n），B（3，n），若点C（﹣1．y₁），D（0，y₂），E（6，y₃）也在该二次函数图象上，则下列结论正确的是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
14. 对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b；如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（）

A、0 B、2 C、3 D、4

查看试题解析
15. 如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG=45°；②AG+DF=FG；③△DEF∽△ABG；④S_△_ABG= $\frac{3}{2}$ S_△_FGH ．其中正确的是（）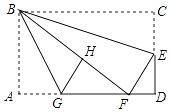

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

16. 分解因式：x²﹣4= ．

查看试题解析
17. 不等式3x﹣2＞2x﹣1的解集是．

查看试题解析
18. 如图，三角板的直角顶点在直线l上，若∠1=70°，则∠2= ．

查看试题解析
19.
一艘轮船在小岛A的北偏东60°距小岛80海里的B处，沿正西方向航行2小时后到达小岛的北偏西45°的C处，则该船行驶的速度为海里/小时．

查看试题解析
20. 一只小狗在如图所示的矩形草地ABCD内自由的玩耍，点P是矩形的边CD上一点，点E、点F分别为PA，PB的中点，连接EF，则这只小狗跑到△PEF内的概率是．

查看试题解析
21.
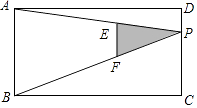如图，直线y= $\frac{4}{3}$ x与双曲线y= $\frac{k}{x}$ （x＞0）交于点A，将直线y= $\frac{4}{3}$ x向下平移个6单位后，与双曲线y= $\frac{k}{x}$ （x＞0）交于点B，与x轴交于点C，则C点的坐标为；若 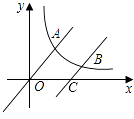$\frac{A O}{B C}$ =2，则k= ．

查看试题解析

三、解答题

22. 完成下列各题：

(1)、计算：2^﹣¹﹣（4﹣π）⁰+ $\frac{1}{2}$

(2)、解方程： $\frac{1}{x - 2}$ = $\frac{3}{2 x + 1}$ ．

查看试题解析
23. 完成下列各题：

(1)、如图，已知直线AB与⊙O相切于点C，且AC=BC，求证：OA=OB．

(2)、如图，矩形ABCD的两条对角线相交于点O，∠AOD=120°，AB=3，求AC的长．

查看试题解析
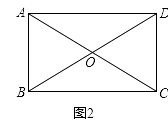24. 某汽车专卖店销售A，B两种型号的新能源汽车．上周售出I辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．求每辆A型车和B型车的售价各为多少元．

查看试题解析
25. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况，在全校范围内随机抽查部分学生，对他们喜爱的体育项目（每人只选一项）进行了问卷调查，将统计数据绘制成如图两幅不完整统计图，请根据图中提供的信息解答下列各题．

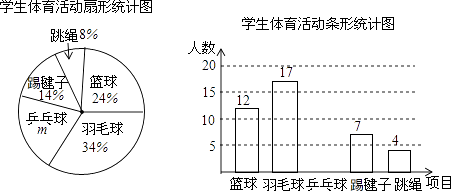(1)、本次问卷调查共抽查了名学生；

(2)、请补全条形统计图；

(3)、请你估计该校约有名学生最喜爱打篮球；

(4)、学校准备从喜欢跳绳活动的4人（三男一女）中随机选取2人进行体能测试，请利用列表或树状图的方法，求抽到一男一女的概率．

查看试题解析
26.
如图，反比例函数y= $\frac{m}{x}$ （x＞0）与一次函数y=kx+6 $\sqrt{3}$ 交于点C（2，4 $\sqrt{3}$ ），一次函数图象与两坐标轴分别交于点A和点B，动点P从点A出发，沿AB以每秒1个单位长度的速度向点B运动；同时，动点Q从点O出发，沿OA以相同的速度向点A运动，运动时间为t秒（0＜t≤6），以点P为圆心，PA为半径的⊙P与AB交于点M，与OA交于点N，连接MN、MQ．

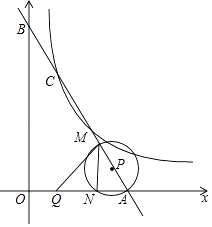(1)、求m与k的值；

(2)、当t为何值时，点Q与点N重合；

(3)、若△MNQ的面积为S，试求S与t的函数关系式．

查看试题解析
27. 在△ABC中，AB=AC，点D为直线BC上一动点（点D不与B、C重合）以AD为边作正方形ADEF，使∠DAF=∠BAC，连接CF．

(1)、
如图1，当点D在线段BC上时，求证：BD=CF；

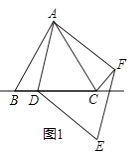(2)、
如图2，当点D在线段BC的延长线上，且∠BAC=90°时．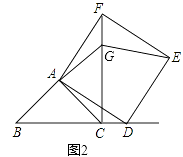
①问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
②延长BA交CF于点G，连接GE，若AB=2 $\sqrt{2}$ ，CD=BC，请求出GE的长．

查看试题解析
28.
如图，抛物线y=ax²+bx﹣4与x轴交于点A（2，0）和点B，与y轴交于点C，顶点为点D，对称轴为直线x=﹣1，点E为线段AC的中点，点F为x轴上一动点．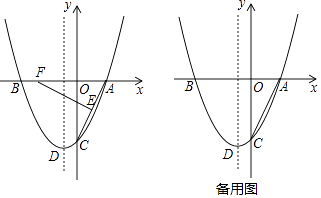

(1)、直接写出点B的坐标，并求出抛物线的函数关系式；

(2)、当点F的横坐标为﹣3时，线段EF上存在点H，使△CDH的周长最小，请求出点H，使△CDH的周长最小，请求出点H的坐标；

(3)、在y轴左侧的抛物线上是否存在点P，使以P，F，C，D为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

	甲	乙	丙	丁
平均数 x（cm）	561	560	561	560
方差s²（cm²）	35	35	155	165