-
1、下列各式中,是分式的是( )A、 B、 C、 D、
-
2、定义:若一个凸四边形的对角线相等,那么我们把这个凸四边形叫作“等线四边形”.
 (1)、以下四边形中,是“等线四边形”的为_______.(填序号)
(1)、以下四边形中,是“等线四边形”的为_______.(填序号)平行四边形;矩形;菱形;正方形.
(2)、如图 , 在正方形中, , 分别为 , 上的点,且 , 连接 , . 求证:四边形为“等线四边形”.(3)、如图 , 在中, , .请用无刻度的直尺和圆规作的垂直平分线(保留作图痕迹,不写作法);
在的条件下,为直线上一点,若以点为顶点的四边形是“等线四边形”,直接写出这个“等线四边形”的面积.
-
3、利用相似三角形可以计算某些不能直接测量的物体的高度,某校“综合与实践”小组的同学把“测量学校旗杆的高度”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下活动报告.根据上面活动报告,解答下列问题:
活动课题
测量学校旗杆的高度
活动目的
利用相似三角形知识解决实际问题
活动工具
皮尺、镜子、标杆等
测量方案
方案:利用影子
方案:利用镜子
方案:利用标杆
测量示意图



测量过程
在同一时刻,小组同学测得身高为米的小乐的影长为米,同时测得旗杆的影长为米.
小慧在她脚下放置镜子 , 然后向后退,直到她刚好在镜子中看到旗杆顶部 . 小组同学测得小慧的眼睛距离地面的高度为米,小慧到镜子的距离为米,旗杆到镜子的距离为米.
小智在他前面立一根标杆 , 当小智的眼睛、标杆顶部、旗杆顶部在同一直线上时,小组同学测得标杆高为米,小智的眼睛距离地面的高度为米,小智与旗杆之间的距离为米,小智与标杆之间的距离为米.
计算结果
. ..
. ..
. ..
反思
. ..
. ..
. ..
(1)、利用方案测得旗杆的高度为___________米;(2)、请将方案的测量示意图补充完整,并求出旗杆的高度;(3)、请利用方案帮小智计算旗杆的高度. -
4、如图,在四边形中,平分 , 且 .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
5、已知关于的方程有两个不等实数根.(1)、求的取值范围;(2)、若方程的两根为 , 且 , 求的值.
-
6、数学兴趣活动课上,小轩和小辉玩抽卡片游戏,如图,他们制作了5张卡片,除正面不同外,其形状、大小、质地和背面图案都完全相同.小轩将它们背面朝上,洗匀后摆放在桌面上.
 (1)、若小轩从中随机抽取一张卡片,抽到的是“高陵果子”的概率是______.(2)、若规定:小轩从中随机抽取一张卡片(不放回),小辉再从中随机抽取一张卡片,若这两张卡片中没有水果,则小轩赢,否则小辉赢.请你用列表或画树状图的方法说明这个游戏是否公平?(注:水果是卡片D,E)
(1)、若小轩从中随机抽取一张卡片,抽到的是“高陵果子”的概率是______.(2)、若规定:小轩从中随机抽取一张卡片(不放回),小辉再从中随机抽取一张卡片,若这两张卡片中没有水果,则小轩赢,否则小辉赢.请你用列表或画树状图的方法说明这个游戏是否公平?(注:水果是卡片D,E) -
7、用适当的方法解下列方程.(1)、(2)、
-
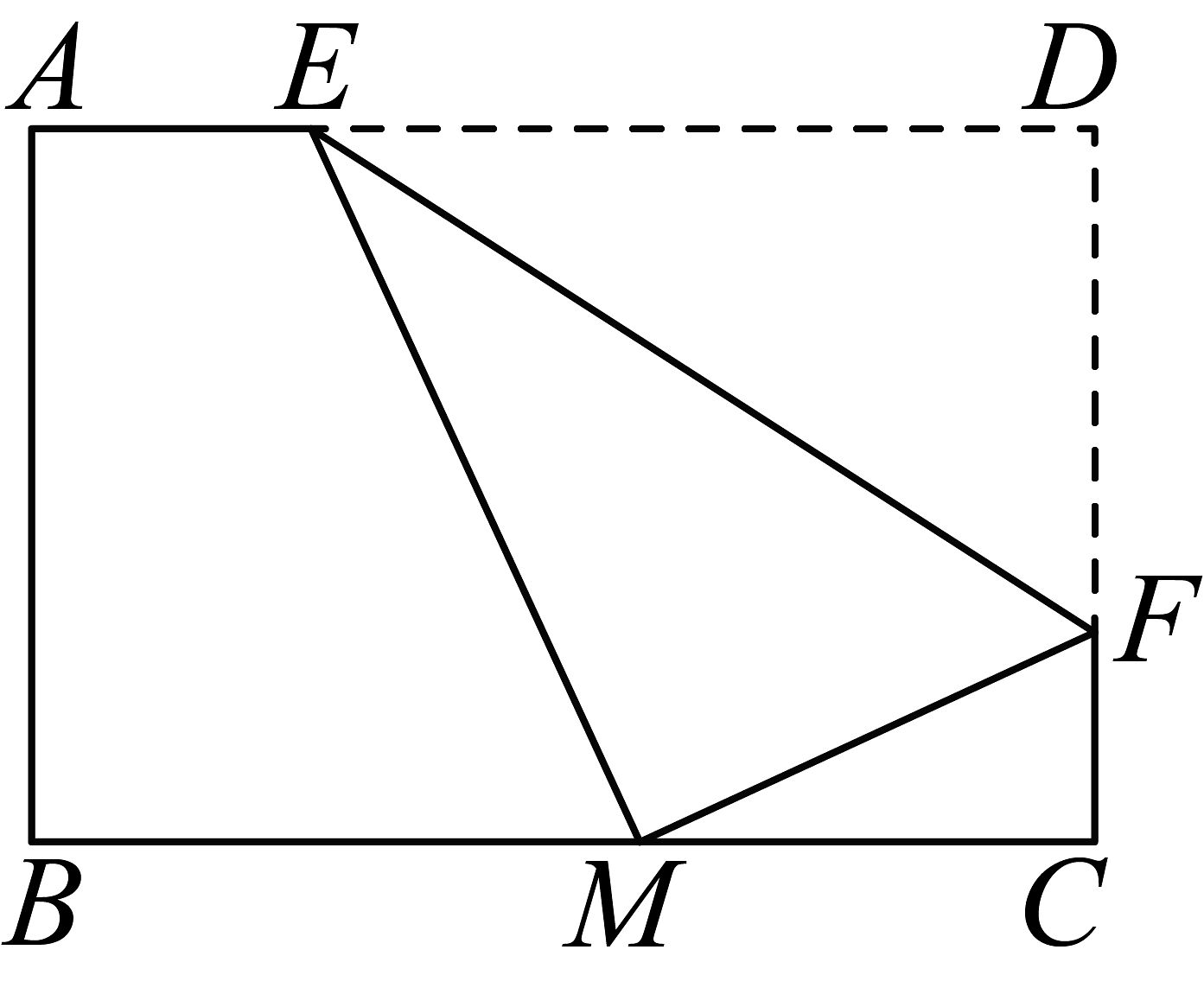
8、如图,将矩形纸片沿边折叠,使点在边中点处.若 , 则 .
-
9、在“霍童线狮”表演中,艺人操控“线狮”在舞台上呈现精彩姿态,舞台上方的灯光照射在“线狮”上,形成的影子属于 , (填写“中心投影”或“平行投影”)
-
10、如图,与是位似图形,且位似中心为 , , 若的周长为 , 则的周长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如果等腰的两边长分别是方程的两个根,则的周长为( )A、12 B、9 C、12或9 D、10
-
12、绿豆芽,为豆科植物绿豆的种子经浸泡后发出的嫩芽,绿豆在发芽过程中,维生素C会增加很多,而且部分蛋白质也会分解为各种人体所需的氨基酸,可达到绿豆原含量的七倍,所以绿豆芽的营养价值比绿豆更大.某农产品生产基地用一批绿豆种子制作绿豆芽,通过大量重复试验,发现这批绿豆种子的发芽率在0.95附近波动,估计这样的绿豆种子中发芽的有( )A、 B、 C、 D、
-
13、如图,点C是线段的黄金分割点(),若长为2,则线段的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、在复习特殊的平行四边形时, 某小组同学画出了如下关系图, 组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是( )
 A、①,对角相等 B、②,对角线互相垂直 C、③,有一组邻边相等 D、④,有一个角是直角
A、①,对角相等 B、②,对角线互相垂直 C、③,有一组邻边相等 D、④,有一个角是直角 -
15、如图是一个长方体从中间去掉一个圆柱得到的几何体,则该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
16、如图,已知直线与x轴交于点A,与y轴交于点C,抛物线经过A,C两点,且与x轴的另一个交点为B,对称轴为直线
 (1)、求抛物线的表达式;(2)、是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,点Q在平面上,以点A,C,P,Q为顶点作菱形,请直接写出符合题意的P点的坐标.
(1)、求抛物线的表达式;(2)、是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,点Q在平面上,以点A,C,P,Q为顶点作菱形,请直接写出符合题意的P点的坐标. -
17、通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的投影称为中心投影. 如图,河对岸有一灯杆 , 在灯光下,小明在点 D 处测得自己的影长 , 沿方向前进到达点F处测得自己的影长 . 已知小明的身高为 ,求灯杆的高度.

-
18、已知关于x的一元二次方程有两个实数根.(1)、求k的取值范围;(2)、设该方程的两个实数根分别为 , , 若 , 满足 , 请求出k的值.
-
19、某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
 (1)、在这次研究中,一共调查了 名学生;(2)、补全条形统计图,并计算阅读部分圆心角是(3)、在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是多少?
(1)、在这次研究中,一共调查了 名学生;(2)、补全条形统计图,并计算阅读部分圆心角是(3)、在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是多少? -
20、(1)解方程:
(2)已知(),求的值.