-
1、 某区准备组织部分学校的中小学生到A , B , C , D , E五个景区“一日游”,每名学生只能在五个景区中任选一个.为估计到各景区旅游的人数,随机抽取这些学校的部分学生,进行了“五个景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
 (1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为人,请估计到A景区旅游的人数.
(1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为人,请估计到A景区旅游的人数. -
2、 如图,已知: , , 那么直线与的位置关系如何?并说明理由.
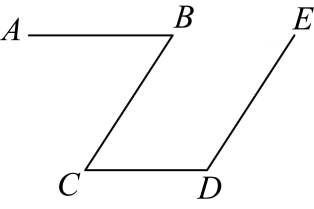
答: ▲ .
理由:(已知)
▲ ( )
(已知)
▲ ( )
▲ ( )
-
3、(1)、计算:;(2)、解方程组: .
-
4、 若不等式组无解,则m的取值范围是 .
-
5、 不等式解集是 .
-
6、 如图,在平面直角坐标系中,从点 , , 依此扩展下去,则的坐标为( )
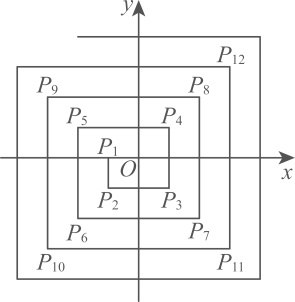 A、 B、 C、 D、
A、 B、 C、 D、 -
7、 如图,点在的延长线上,下列条件能判断的是( )
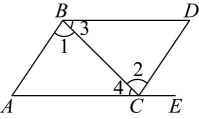 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 下列调查中,适宜采用全面调查方式的是( )A、旅客上飞机前的安全检查 B、对广州市七年级学生身高现状的调查 C、对某品牌食品安全的调查 D、对一批灯管使用寿命的检查
-
9、 一个正方形的面积是11,估计它的边长大小在( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间
-
10、 在实数(每两个1之间0的个数依次增加1)中,无理数有( )A、1个 B、2个 C、3个 D、4个
-
11、 下列方程组中,解为的是( )A、 B、 C、 D、
-
12、 已知 , 下列不等式变形中正确的是( )A、 B、 C、 D、
-
13、 下列各图中,与是对顶角的是( )A、
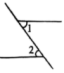 B、
B、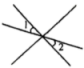 C、
C、 D、
D、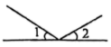
-
14、请阅读下列材料:
问题:已知 求代数式 的值.
小明的做法:根据 得 所以 所以 把 的值整体代入,得x2-4x-7=1-7=-6.即把已知条件适当变形,再整体代入解决问题.
仿照上述方法解决问题:
(1)、已知 求代数式 的值;(2)、已知 求代数式 的值. -
15、已知 则 的值为.
-
16、如图,点P 在数轴上对应的数为x,且点 P在 A,B两点之间.化简:

-
17、(1)、已知x,y是有理数,若 求 xy的平方根;(2)、已知a,b 是等腰△ABC 的两边长,且满足 求△ABC的周长.
-
18、综合与实践

【问题情境】在平面直角坐标系 xOy 中有不重合的两点A(x1 , y1)和B(x2 , y2),小明在学习中发现,若 , 则AB∥y轴,且线段AB 的长度为 若 y2 , 则AB∥x轴,且线段AB的长度为|
(1)、【应用】①若点A(-1,1),B(2,1),则AB 的长度为
②若点C(1,0),CD∥y轴,且 CD=2,则点 D的坐标为.
(2)、【拓展】我们规定:平面直角坐标系中任意不重合的两点M(x1 , y1),N(x2 , y2)之间的折线距离为 例如:图(1)中,点.M(-1,1)与点N(1,-2)之间的折线距离为d(M,N)=|-1-1|+|1-(-2)|=2+3=5.【解决问题】
如图(2),已知E(2,0),若F(-1,-2),则d(E,F)=.
(3)、如图(2),已知E(2,0),H(1,t),若d(E,H)=3,求t的值. -
19、如图,在平面直角坐标系中,点A 的坐标为(2,0),点 B 的坐标为(0,1),将线段AB 平移,使其一个端点到C(3,2),则平移后另一个端点的坐标为.

-
20、如图,正方形ABCD 的各边分别平行于x轴或y轴,蚂蚁甲和蚂蚁乙都由点 E(3,0)出发,同时沿正方形ABCD 的边做环绕运动,蚂蚁甲按顺时针方向以3个单位长度/秒的速度做匀速运动,蚂蚁乙按逆时针方向以 1 个单位长度/秒的速度做匀速运动,则两只蚂蚁出发后的第三次相遇点的坐标是.
