-
1、计算: .
-
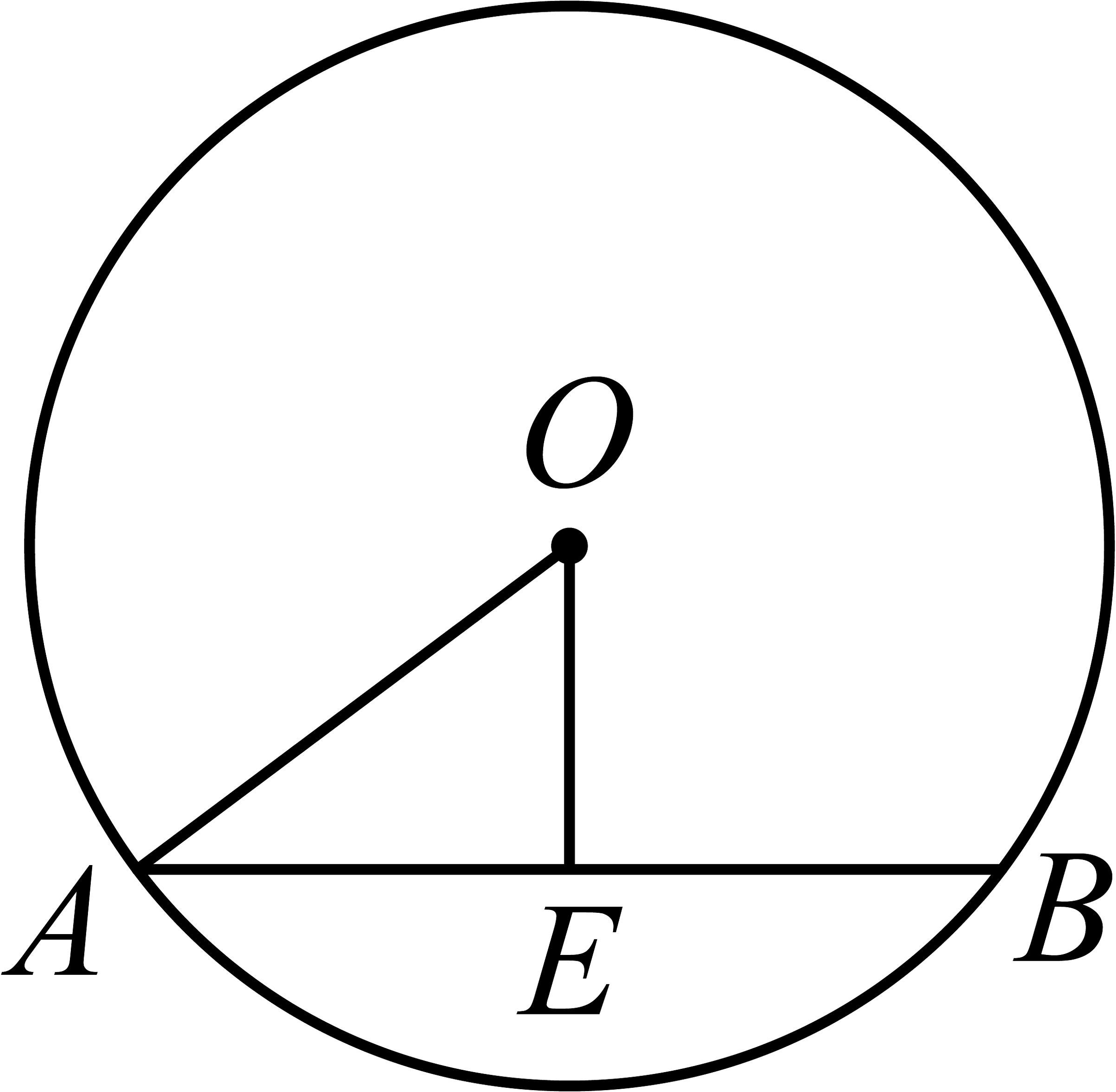
2、如图,于 , 若的半径为 , , 则 .
-
3、函数的图象在每个象限内随的增大而增大,则的取值范围是 .
-
4、已知与关于原点对称,则的值是 .
-
5、如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在正方形顶点上,那么的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知 , 相似比为 , 若的周长是9,则的周长为( ).A、1 B、3 C、6 D、9
-
7、若零下2摄氏度记为 , 则零上2摄氏度记为( ).A、 B、 C、 D、
-
8、如图,在平面直角坐标系中,每个小方格都是边长为1的正方形.已知各顶点在格点上,为坐标原点,点的坐标分别为 , 将绕点按逆时针方向旋转得到 .
 (1)、画出 , 并写出点的坐标;(2)、求的面积.
(1)、画出 , 并写出点的坐标;(2)、求的面积. -
9、如图,抛物线的图象与轴交于两点,与轴交于点 , 顶点为 .
 (1)、求此抛物线的解析式;(2)、在抛物线的对称轴上是否存在点 , 使得的周长最小?若存在,求出点的坐标并计算的周长;若不存在,请说明理由;(3)、设点在第四象限,且在抛物线上,当的面积最大,求此时点的坐标.(直接写出结果)
(1)、求此抛物线的解析式;(2)、在抛物线的对称轴上是否存在点 , 使得的周长最小?若存在,求出点的坐标并计算的周长;若不存在,请说明理由;(3)、设点在第四象限,且在抛物线上,当的面积最大,求此时点的坐标.(直接写出结果) -
10、某商品现在的售价为每件80元,每星期可卖出200件,市场调查反映:如调整价格,每降价1元,每星期要多卖出10件.已知商品的进价为每件50元.(1)、若每件降价x元,单件商品的利润为______元;每星期的销售量为______件(用含x的式子表示);(2)、若每周可获利y元,求y与x的函数关系式;(3)、售价为多少才能使利润最大?并求出最大利润.
-
11、已知内接于为的直径,弦与相交于点 .
 (1)、如图①,若平分 , 连接 , 求和的大小;(2)、如图②,过点作的切线,与的延长线交于点 , 若 , 求的大小.
(1)、如图①,若平分 , 连接 , 求和的大小;(2)、如图②,过点作的切线,与的延长线交于点 , 若 , 求的大小. -
12、已知二次函数与x轴交于A,两点(点A在点B的左侧),与y轴交于点C.(1)、求三点的坐标;(2)、求的面积.
-
13、解下列方程:(1)、;(2)、 .
-
14、如图,已知点 , 若在所给的网格中存在一点 , 使得与垂直且相等.

(1)直接写出点的坐标;
(2)将线段绕某一点旋转一定角度,使其与线段重合,则这个旋转中心的坐标为 .
-
15、在平面直角坐标系中,点坐标为 , 连接 , 将绕点逆时针旋转后,得到 , 则点的坐标为 .
-
16、已知二次函数的图象开口向下,则的取值范围是 .
-
17、如图,在⊙O中, , , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元,设平均每月降低的百分率为 , 根据题意列出的方程是( )A、 B、 C、 D、
-
19、用配方法解一元二次方程时,下列变形正确的是( )A、 B、 C、 D、
-
20、下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、