相关试卷

1、一个两位数，十位上的数字是 $b$ ，个位上的数字是 $a$ ，这个两位数是（）

A、 $a + b$ B、 $10 (a + b)$ C、 $10 a + b$ D、 $10 b + a$

查看解析
2、在 $3.14$ ， 2024， $- \frac{22}{7}$ ， $π$ 四个数中有理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看解析
3、南岸区是一个充满生机和活力的市区，它古老而又年轻，区域内人口约为1200000人．则1200000用科学记数法可表示为（　　）

A、 $120 \times 10^{4}$ B、 $12 \times 10^{5}$ C、 $1.2 \times 10^{6}$ D、 $0.12 \times 10^{7}$

查看解析
4、如图，在直角三角形ABC中，∠C=90°，∠B=60°，AB=8cm，E、F分别为边AC、AB的中点．
（1）求∠A的度数；
（2）求EF和AE的长．

查看解析
5、已知直线 $y_{1} = m x + 3 n - 1$ 与直线 $y_{2} = (m - 1) x - 2 n + 2$ ．

(1)、如果 $m = - 1, n = 1$ ，当x取何值时， $y_{1} > y_{2}$ ？

(2)、如果两条直线相交于点A，A点的横坐标x满足 $- 1 < x < 13$ ，求整数n的值．

查看解析
6、如图，在ABCD中，AB∥CD，AD＝BC，∠B＝60°，AC平分∠DAB．
(1)求∠ACB的度数；
(2)如果AD＝1，请直接写出向量 $\overset{⃑}{D C}$ 和向量 $\overset{⃑}{B C} + \overset{⃑}{C D} + \overset{⃑}{D A}$ 的模．

查看解析
7、在三角形 $A B C$ 中，点 $D, E, F$ 分别是 $B C, A B, A C$ 的中点， $A H ⊥ B C$ 于点 $H$ ，若 $∠ D E F = 50^{\circ}$ ，则 $∠ C F H =$ .

查看解析
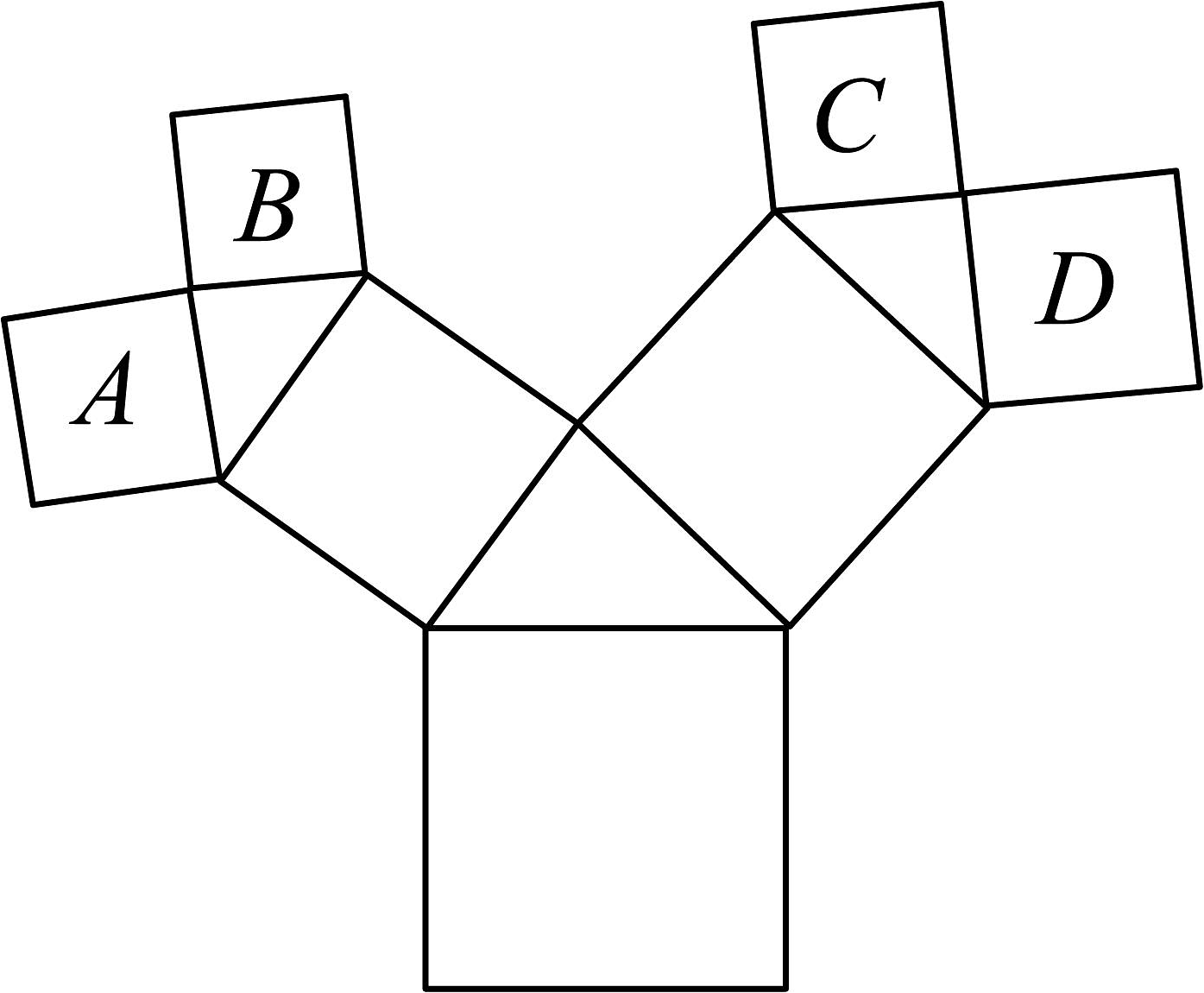
8、如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的面积为49，则正方形A、B、C、D的面积之和为．

查看解析
9、计算：
（1） $\sqrt{8} - | \sqrt{2} - 2 | + \sqrt{{(- 2)}^{2}}$ ；
（2） $\frac{3 - \sqrt{3}}{\sqrt{3}} + (3 + \sqrt{3}) (3 - \sqrt{3})$

查看解析
10、在综合与实践课上，老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
（1）奋进小组用图1中的矩形纸片ABCD，按照如图2所示的方式，将矩形纸片沿对角线AC折叠，使点B落在点 $B^{'}$ 处，则 $△ A D C$ 与 $△ A B^{'} C$ 重合部分的三角形的类型是________.
（2）勤学小组将图2中的纸片展平，再次折叠，如图3，使点A与点C重合，折痕为EF，然后展平，则以点A、F、C、E为顶点的四边形是什么特殊四边形？请说明理由．
（3）创新小组用图4中的矩形纸片ABCD进行操作，其中 $A D = 8 cm$ ， $A B = 6 cm$ ，先沿对角线BD对折，点C落在点 $C^{'}$ 的位置， $B C^{'}$ 交AD于点G，再按照如图5所示的方式折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M．则EM的长为________cm.

查看解析
11、某校团委积极响应南充市“书香天府万卷南充”全民阅读活动，号召全校学生积极捐献图书共建“书香校园”．八（1）班40名同学都捐献了图书，全班40名同学共捐图书320册．班长统计了全班捐书情况如表：
册数
4
5
6
7
8
50
人数
6
8
15
2
（1）分别求出该班级捐献7册图书和8册图书的人数；
（2）请算出捐书册数的平均数、中位数和众数，并判断其中哪些统计量不能反映该班同学捐书册数的一般状况，说明理由

查看解析
12、一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：
点 $P (x_{0}, y_{0})$ 到直线 $A x + B y + C = 0$ 的距离 $(d)$ 公式是： $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$
如：求：点 $P (1,1)$ 到直线 $2 x + 6 y - 9 = 0$ 的距离．
解：由点到直线的距离公式，得 $d = \frac{| 2 \times 1 + 6 \times 1 - 9 |}{\sqrt{2^{2} + 6^{2}}} = \frac{1}{\sqrt{40}} = \frac{\sqrt{10}}{20}$
根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．
则两条平行线 $l_{1}$ ： $2 x + 3 y = 8$ 和 $l_{2}$ ： $2 x + 3 y + 18 = 0$ 间的距离是．

查看解析
13、如图，正方形ABCD的周长是16，P是对角线AC上的个动点，E是CD的中点，则PE+PD的最小值为( )

A、2 $\sqrt{5}$ B、2 $\sqrt{3}$ C、2 $\sqrt{2}$ D、4

查看解析
14、若函数 $y = \frac{1}{x - 1}$ 有意义，则（）

A、 $x > 1$ B、 $x < 1$ C、 $x = 1$ D、 $x \neq 1$

查看解析

15、某出租车公司推出

A

专车和

B

快车两种出租车，它们的收费方式如下：

$A$ 专车： $3$ 千米以内收费 $10$ 元，超过 $3$ 千米的部分每千米收费 $2.5$ 元，不收其他费用；

$B$ 快车：

计费项目	起步价	里程费	远途费
计费价格	$8$ 元	2元/千米	1元/千米
注：车费由起步价、里程费、远途费三部分组成，其中起步价包含里程 $2$ 千米；里程大于 $2$ 千米的部分按计价标准收取里程费；远途费的收取方式为：行车不超过12千米，不收远途费，超过 $12$ 千米的，超出的部分每千米加收 $1$ 元．

(1)、如果乘车路程是

8

千米，使用

A

专车、

B

快车出行各需支付费用多少元？

(2)、如果乘车路程是

x (x > 12)

千米，使用

A

专车、

B

快车出行各需支付的费用多少元（用含

x

的式子表示）？

(3)、如果乘车路程是

y

千米时，使用

B

快车出行的费用比使用

A

专车出行省4元，求

y

的值．

查看解析

16、定义：对于一个两位数 $x$ ，如果 $x$ 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“相异数”，将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数，将这个新两位数与原两位数求和，同除以11所得的商记为 $S (x)$ ．例如， $a = 15$ ，对调个位数字与十位数字得到的新两位数51，新两位数与原两位数的和为 $15 + 51 = 66$ ，和66除以11的商为 $66 \div 11 = 6$ ，所以 $S (15) = 6$ ．

(1)、计算： $S (72) =$ ____；

(2)、若一个“相异数” $y$ 的十位数字是 $k$ ，个位数字是 $3 (k - 2)$ ，且 $S (y) = 10$ ，求相异数 $y$ ；

(3)、小慧同学发现若 $S (x) = 7$ ，则“相异数” $x$ 的个位数字与十位数字之和一定为7，请判断小慧的发现是否正确？如果正确，说明理由；如果不正确，举出反例．

查看解析
17、手工制作课上，劳动课吴老师组织七年级（2）班的学生用硬纸制作圆柱形茶叶筒．七年级（2）班共有48人，其中男生人数比女生人数少2人，并且每名学生每小时剪筒身55个或剪筒底130个．

(1)、七年级（2）班有男生、女生各多少人？

(2)、七年级（2）班全体同学积极参与制作圆柱形茶叶筒，要求用一个筒身配两个筒底，为了使每小时剪出的筒身与筒底刚好配套，应该分配多少名学生剪筒身，多少名学生剪筒底？

查看解析
18、小明连续记录了他家私家车 $7$ 天中每天行驶的路程（如表），以 $50 km$ 为标准，多于 $50 km$ 的记为“ $+$ ”，不足 $50 km$ 的记为“ $-$ ”

第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程 $(km)$
$- 8$
$- 10$
$- 14$
$10$
$- 16$
$+ 31$
$+ 7$

(1)、在这七天中，最远与最近路程差是多少千米？

(2)、若行驶 $1 km$ 需用汽油 $0.08$ 升，汽油价格为 $8$ 元 $/$ 升，请计算小明家这 $7$ 天的汽油费用是多少元？

查看解析
19、如图所示的图形由一个正方形和一个长方形组成．

(1)、求该图形的面积（用含 $x$ 的式子表示）；

(2)、若 $x = 1$ ，求该图形的面积．

查看解析
20、画一条数轴，并把 $- 3$ ， $1$ ， $- 1 \frac{1}{2}$ ， $3$ 表示在数轴上，并用“ $<$ ”连接起来．

查看解析

上一页 1156 1157 1158 1159 1160 下一页跳转

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
路程 $(km)$	$- 8$	$- 10$	$- 14$	$10$	$- 16$	$+ 31$	$+ 7$

册数	4	5	6	7	8	50
人数	6	8	15			2