-
1、下表是我国几个城市某年一月份的平均气温,其中气温最低的城市是( )
城市 北京 武汉 广州 哈尔滨 平均气温(单位:℃) -4.6 3.8 13.1 -19.4 A、哈尔滨 B、广州 C、武汉 D、北京 -
2、如图,点M、点C在线段上,M是线段的中点, , 若 , 则的长为( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1 -
3、比较大小:(填“”或“”或“”).
-
4、如图1,四边形为正方形,E为对角线上一点,连接 , .
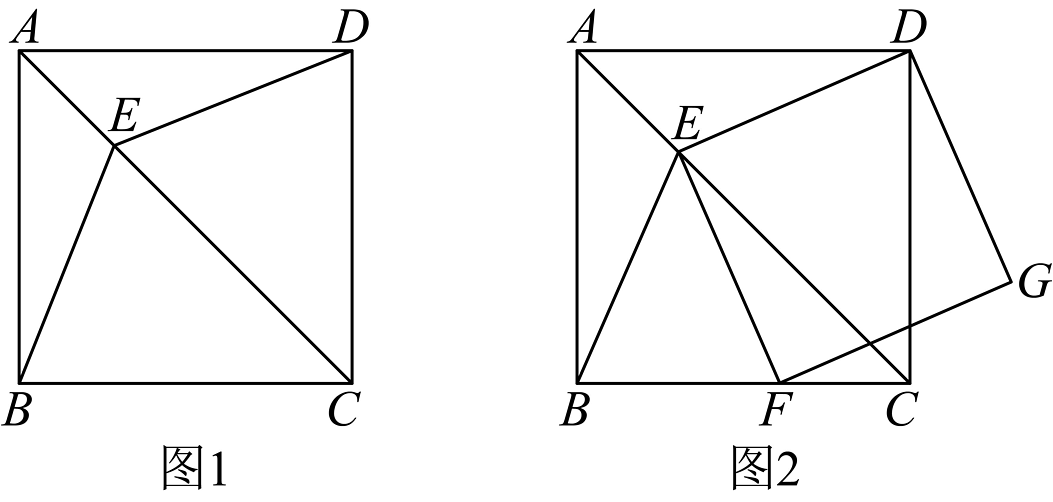 (1)、求证:;(2)、如图2,过点E作 , 交边于点F,以 , 为邻边作矩形 , 连接 .
(1)、求证:;(2)、如图2,过点E作 , 交边于点F,以 , 为邻边作矩形 , 连接 .①求证:矩形是正方形;
②若正方形的边长为 , , 求正方形的边长.
-
5、一个立体图形的展开图如图所示,这个立体图形是 .

-
6、将抛物线先向左平移1个单位,再向下平移3个单位,所得的抛物线解析式是( )A、 B、 C、 D、
-
7、一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.
小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是 ;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
-
8、小明问小白:“你知道为什么任何无限循环小数都可以写成分数形式吗?”看着小白一脸的茫然,小明热心地为小白讲解:
[小明提出问题]利用一元一次方程将化成分数.
[小明解答]解:设 , 方程两边都乘以 , 可得由 , 可知 , 即 , 可解得 , 即 .
(1)、请你仿照小明的方法把下列两个小数化成分数:① ;② ;(2)、请将化为分数,并写出解答过程:(3)、你能通过上述方法判断是否正确吗?说明你的理由. -
9、2024年东港市某中学要建一长方形停车场,其中一面靠墙,其他三面用护栏围起,已知长方形停车场的长为米,宽比长少米.
 (1)、用 , 表示长方形停车场的宽.(2)、求护栏的总长度.(3)、若 , , 每米护栏造价70元,求建此停车场所需的费用.
(1)、用 , 表示长方形停车场的宽.(2)、求护栏的总长度.(3)、若 , , 每米护栏造价70元,求建此停车场所需的费用. -
10、如图是一组有规律的图案,它们是由边长相同的小正方形组成的,其中部分小正方形涂有阴影,依此规律,第个图案中有个阴影小正方形(用含有的代数式表示).

-
11、甲、乙两个足球队连续打对抗赛,规定胜一场得分,平一场得分,负一场得分,共赛场,甲队保持不败,得分,甲队胜场.
-
12、下列四个几何体中,是圆柱的是( )A、
 B、
B、 C、
C、 D、
D、
-
13、如图,数轴上被墨水遮盖的数可能为( )
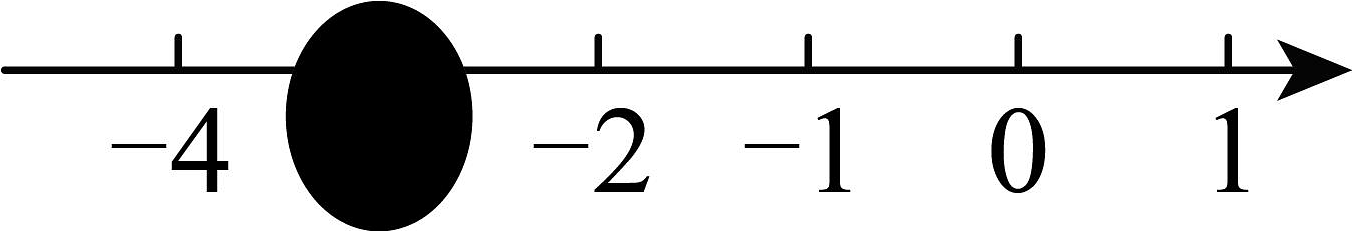 A、 B、 C、 D、
A、 B、 C、 D、 -
14、下列图形中,属于立体图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
15、比-3℃低7℃的温度是( )A、4℃ B、-4℃ C、10℃ D、=10℃
-
16、同学们在操场上进行铅球训练,小明尝试利用数学模型研究铅球的运动情况,其运动路径可看作抛物线的一部分,以地面水平方向为x轴,出手点与地面的垂线为y轴,单位长度为 , 建立了如图所示的平面直角坐标系.小明在投掷铅球时,铅球出手时铅球离地面的高度为 , 铅球落地时,离出手点的水平距离是 , 铅球运行的水平距离为时达到最大高度.
 (1)、求该铅球运行路径所在抛物线的表达式;(2)、当铅球距出手点的水平距离为时,求铅球距离地面的高度;(3)、小红在投掷铅球时,铅球出手时和落地时的位置与小明的相同,但小红投掷的铅球在距出手点水平距离为时达到最大高度.假设铅球运行的水平距离相同时,小红投掷铅球时铅球的所在位置与小明投掷铅球时铅球所在位置的高度差为 , 求的最大值及此时铅球运行的水平距离.
(1)、求该铅球运行路径所在抛物线的表达式;(2)、当铅球距出手点的水平距离为时,求铅球距离地面的高度;(3)、小红在投掷铅球时,铅球出手时和落地时的位置与小明的相同,但小红投掷的铅球在距出手点水平距离为时达到最大高度.假设铅球运行的水平距离相同时,小红投掷铅球时铅球的所在位置与小明投掷铅球时铅球所在位置的高度差为 , 求的最大值及此时铅球运行的水平距离. -
17、如图是由小正方形组成的的网格,正方形的顶点称为格点,点A,B,C均为格点,仅用无刻度的直尺在给定网格中完成画图,每个画图任务的画线不得超过三条.
 (1)、在图(1)中,线段绕点B逆时针旋转后得到线段 , 画线段;(2)、观察发现,(1)中 , 都是直角三角形,在图(1)中,再画所有不同于M的点N使 , 都是直角三角形;(3)、在图(2)中,先画的中点D,再画线段 , 使 , 且;(4)、在图(2)中,P是线段的延长线上一点,在线段上画点Q,使 .
(1)、在图(1)中,线段绕点B逆时针旋转后得到线段 , 画线段;(2)、观察发现,(1)中 , 都是直角三角形,在图(1)中,再画所有不同于M的点N使 , 都是直角三角形;(3)、在图(2)中,先画的中点D,再画线段 , 使 , 且;(4)、在图(2)中,P是线段的延长线上一点,在线段上画点Q,使 . -
18、某学校组织以“珍爱生命”为主题的安全教育知识竞赛,发现全校学生的成绩均不低于分(满分分),现从中随机抽取名学生的成绩进行整理和分析(成绩得分用表示,共分成四组),并绘制成如下的成绩分组统计表和扇形统计图,其中“”这组的数据如下: , , , , , , , , , , , , , , .
安全意识主题知识竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分

请根据以上信息,解答下列问题:
(1)、 ;(2)、这名学生的平均成绩是 分,中位数是 分;(3)、若学生竞赛成绩达到分以上(含分)为优秀,请你估计全校名学生中竞赛成绩优秀的学生人数. -
19、关于的一元二次方程有一个根是 , 求的值及方程的另一个根.
-
20、抛物线(为常数)经过三点,与轴的交点在正半轴.下列结论:①;②;③抛物线与直线的一个交点的横坐标为 , 若 , 则;④当时,则方程必有两个不相等的实数根.其中正确的是 (填写序号).